群馬大学(医学) 2024年　問題3


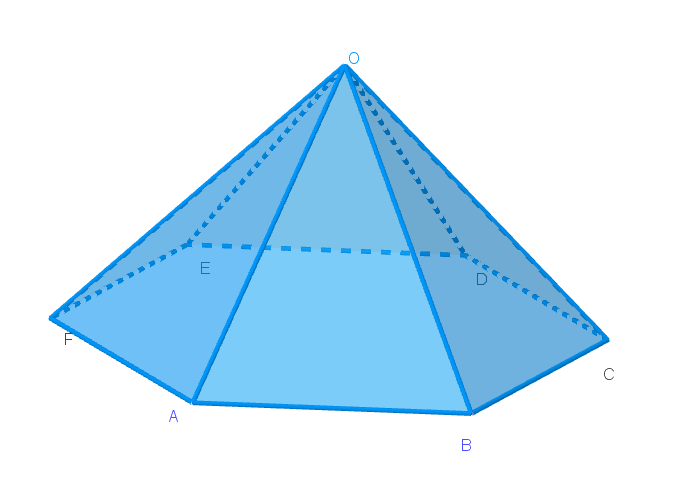
$六角錐 \ O=ABCDEF\ は、底面 \ ABCDEF\ が各辺の長さ \ 1\ の正六角形で、$
$\qquad OA=OB=OC=OD=OE=OF=2\ を満たすとする。$
$\vec{OA}=\vec{a},\ \ \vec{OB}=\vec{b},\ \ \vec{OC}=\vec{c},\ \ \vec{OE}=\vec{e} \ \ とする。以下の問に答えよ。$
$(1)\ \ 内積\ \vec{a} \cdot \vec{b},\ および \ \ \vec{a} \cdot \vec{c}\ \ を求めよ。$
$(2)\ \ \vec{b}\ を \ \vec{a}, \ \vec{c}, \ \vec{e} \ \ を用いて表せ。$
$\quad 辺OA\ の中点を \ M\ とし、辺OB\ 上に点P\ を、MP+PC \ \ が最小になるようにとる。$
$(3)\ \ OP\ の長さを求めよ。$
$(4)\ \ P\ は \ 3\ 点 \ M,\ C,\ E\ の定める平面上にないことを示せよ。$


(1)

　

$\triangle OAB \ は \ AB=1,\ \ OA=OB=2\ \ の二等辺三角形だから$

$余弦定理を用いて$

$\cos \angle AOB=\cfrac{OA^2+OB^2-AB^2}{2OA \cdot OB}=\cfrac{2^2+2^2-1^2}{2 \times 2 \times 2}=\cfrac{7}{8}$

$よって$

$\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\cos \angle AOB=2 \times 2 \times \cfrac{7}{8}=\cfrac{7}{2}$

　

$底面の正六角形の中心を \ H\ とすると$

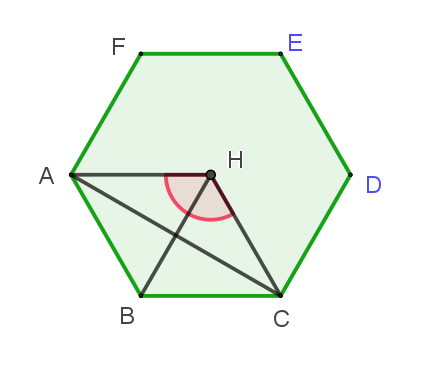
$\triangle HAB,\ \ \triangle HBC \ はともに正三角形だから$

$HA=HC=1,\ \ \angle AHC=\cfrac{2}{3}\pi$

$AC^2=HA^2+HC^2-2HA \cdot HC \cdot \cos \dfrac{2}{3}\pi=1+1-2 \times (-\cfrac{1}{2})=3$

$よって \quad AC=\sqrt{3}$

$\triangle OAC \ に余弦定理を用いて$

$\cos \angle AOC=\cfrac{OA^2+OC^2-AC^2}{2OA \cdot OC}=\cfrac{2^2+2^2-3}{2 \times 2 \times 2}=\cfrac{5}{8}$

$\vec{a} \cdot \vec{c}=|\vec{a}||\vec{c}|\cos \angle AOC=2 \times 2 \times \cfrac{5}{8}=\cfrac{5}{2}$


(2)


$底面の正六角形 \ ABCDEF \ において$

$\vec{AD}=2\vec{BC} \quad だから$

$\vec{OD}-\vec{OA}=2(\vec{OC}-\vec{OB})$

$\vec{d}-\vec{a}=2(\vec{c}-\vec{b})$

$\vec{d}=\vec{a}-2\vec{b}+2\vec{c} \hspace{5em}①$

$同様に$

$\vec{BE}=2\vec{CD} \quad だから$

$\vec{OE}-\vec{OB}=2(\vec{OD}-\vec{OC})$

$\vec{e}-\vec{b}=2(\vec{d}-\vec{c})$

$①を代入して$

$\vec{e}-\vec{b}=2(\vec{a}-2\vec{b}+2\vec{c})-2\vec{c}$

$3\vec{b}=2\vec{a}+2\vec{c}-\vec{e}$

$\vec{b}=\cfrac{2}{3}\vec{a}+\cfrac{2}{3}\vec{c}-\cfrac{1}{3}\vec{e}$


(3)

　

$MP+PC \ \ が最小になるのは、二等辺三角形 \ OAB\ と$

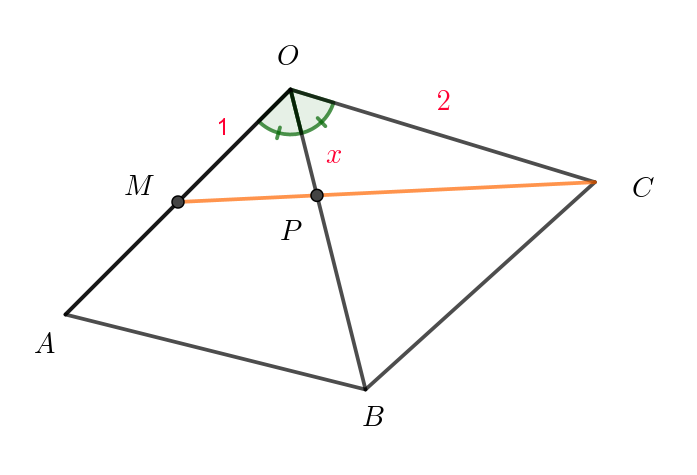
$二等辺三角形 \ OBC\ を平面上に展開したとき$

$3\ 点M, \ P, \ C\ が一直線上に並ぶときである。$

$このとき、OP=x \ \ とおく。$

$\triangle OMP \ と \ \triangle OCP \ に余弦定理を用いて$

\begin{eqnarray*} MP^2 &=&1^2+x^2-2 \times 1 \times x \times \cos \angle MOP\\ \\ &=&1+x^2-2x \times \cfrac{7}{8}\\ \\ &=&x^2-\cfrac{7}{4}x +1 \end{eqnarray*} \begin{eqnarray*} CP^2 &=&2^2+x^2-2 \times 2 \times x \times \cos \angle COP\\ \\ &=&4+x^2-4x \times \cfrac{7}{8}\\ \\ &=&x^2-\cfrac{7}{2}x +4 \end{eqnarray*} $また、\triangle OMC \quad において、\angle MOP=\angle COP \quad だから、角の二等分線と辺の比の関係より$

$OM:OC=MP:CP \quad よって\quad 1:2=MP:CP$

$CP=2MP$

$よって$

$x^2-\cfrac{7}{2}x +4=4\big(x^2-\cfrac{7}{4}x +1\big)$

$3x^2-\cfrac{7}{2}x=0$

$x \ne 0 \quad だから \quad x=OP=\cfrac{7}{6}$


(4)

　

$点Pが\ 3\ 点 \ M,\ C,\ E\ の定める平面上にあるとすると$

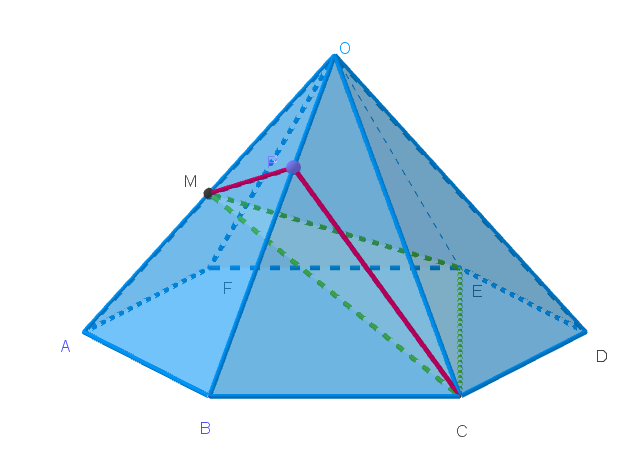
$\vec{MP}=k\vec{MC}+l\vec{ME} \ \ を満たす実数 \ k,\ l\ が存在するから$

\begin{eqnarray*} \vec{MP} &=&k(\vec{c}-\dfrac{1}{2}\vec{a})+l(\vec{e}-\dfrac{1}{2}\vec{a})\\ \\ &=&-\cfrac{1}{2}(k+l)\vec{a}+k\vec{c}+l\vec{e} \end{eqnarray*}
$一方$

$(3)より \quad \vec{OP}=\cfrac{\dfrac{{7}}{6}}{2}\vec{OB}=\cfrac{7}{12}\vec{b}$

\begin{eqnarray*} \vec{MP} &=&\vec{OP}-\vec{OM}\\ \\ &=&\cfrac{7}{12}\vec{b}-\cfrac{1}{2}\vec{a}\\ \\ &=&\cfrac{7}{12}\big(\cfrac{2}{3}\vec{a}+\cfrac{2}{3}\vec{c}-\cfrac{1}{3}\vec{e}\big)-\cfrac{1}{2}\vec{a}\\ \\ &=&-\cfrac{2}{9}\vec{a}+\cfrac{7}{18}\vec{c}-\cfrac{7}{36}{e} \\ \end{eqnarray*} $したがって$

$-\cfrac{1}{2}(k+l)\vec{a}+k\vec{c}+l\vec{e}=-\cfrac{2}{9}\vec{a}+\cfrac{7}{18}\vec{c}-\cfrac{7}{36}{e}$

$\vec{c}\ と \ \vec{e}\ の係数を比べて \quad k=\cfrac{7}{18},\quad l=-\cfrac{7}{36}$

$このとき左辺の \ \vec{a}\ の係数は \quad -\cfrac{1}{2} \times (\cfrac{7}{18}-\cfrac{7}{36})=-\cfrac{7}{72}$

$これは右辺の \ \vec{a}\ の係数に一致しない。$

$したがって点Pは\ 3\ 点 \ M,\ C,\ E\ の定める平面上にない。$


ページの先頭へ↑




メインメニュー　に戻る