群馬大学(医学) 2024年　問題2


$p,\ q\ を実数の定数とする。x\ についての整式 \ A(x)\ と \ B(x)\ を$
$\qquad A(x)=x^4+2px^3+4x^2+qx+p+2 ,\quad B(x)=x^3+2px^2+3x-2p+q$
$とおく。A(x)\ を \ B(x)\ で割った余りを \ R(x)\ とし、B(x)\ を \ R(x)\ で割った余りを \ S(x)\ とする。$
$以下の問に答えよ。ただし、方程式の解は複素数の範囲で考えることにする。$
$(1)\ \ R(x)\ と \ S(x)\ を求めよ。$
$(2)\ \ \alpha \ を複素数とする。R(\alpha)=S(\alpha)=0\ は、A(\alpha)=B(\alpha)=0 \ であるための必要十分条件であることを示せ。$
$(3)\ \ p=3 \ とする。2\ つの方程式 \ A(x)=0,\ B(x)=0 \ が共通の解を少なくとも \ 1\ つもつような定数 \ q \ の値を$
$\quad すべて求めよ。$
$(4)\ \ 方程式 \ R(x)=0\ が実数解をもたないように、定数 \ p\ の値の範囲を定めよ。さらに \ p\ がその範囲にあると$
$\quad き、2\ つの方程式 \ A(x)=0,\ B(x)=0\ が共通の解を少なくとも \ 1\ つもつように、定数 \ p,\ q\ の値を定めよ。$


(1)

　

$右のように筆算の割り算を行うと$

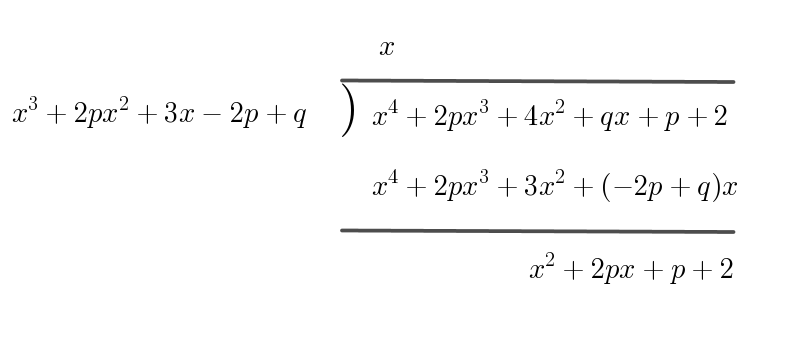
$A(x)\ を \ B(x)\ で割った余り\ R(x)\ は$

$R(x)=x^2+2px+p+2$

　

$B(x)\ を \ R(x)\ で割った余り \ S(x)\ は$

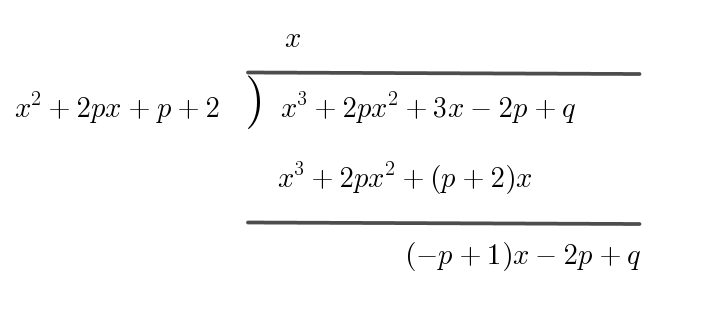
$S(x)=(-p+1)x-2p+q$


(2)


$除法の原理により$

$A(x)=B(x)Q(x)+R(x),\quad B(x)=R(x)Q'(x)+S(x) \ \ (Q(x),\ Q'(x) \ はそれぞれ商) \quad とおけるから$

$A(\alpha)=B(\alpha)Q(\alpha)+R(\alpha),\quad B(\alpha)=R(\alpha)Q'(\alpha)+S(\alpha) $

$必要条件$

$R(\alpha)=S(\alpha)=0 \quad ならば$

$B(\alpha)=R(\alpha)Q'(\alpha)+S(\alpha) =0,\quad A(\alpha)=B(\alpha)Q(\alpha)+R(\alpha)=0$

$十分条件$

$A(\alpha)=B(\alpha)=0 \quad ならば$

$A(\alpha)=B(\alpha)Q(\alpha)+R(\alpha)=0 \quad より \quad 　R(\alpha)=0$

$B(\alpha)=R(\alpha)Q'(\alpha)+S(\alpha) \quad より \quad S(\alpha)=0$


(3)


$p=3 \quad ならば \quad A(x)=x^4+6x^3+4x^2+qx+5 ,\quad B(x)=x^3+6x^2+3x+q-6$

$A(x)=0,\ \ B(x)=0 \ \ の共通の解を \ \alpha \ とすると \quad A(\alpha)=B(\alpha)=0$

$このとき(2)より \quad R(\alpha)=S(\alpha)=0 \quad だから (1)より$

\[ \hspace{1em} \left\{ \begin{array}{l} R(\alpha)=\alpha^2+6\alpha + 5=0 \hspace{5em}①\\ S(\alpha)=-2\alpha +q-6 =0 \hspace{5em}②\\ \end{array} \right. \]
$①より \quad (\alpha +1)(\alpha +5)=0 \qquad \alpha=-1,\ \ -5$

$それぞれ②に代入して$

$\alpha=-1 \ \ のとき \ \ q=4,\qquad \alpha=-5 \ \ のとき \ \ q=-4$


(4)


$(1)より \quad R(x)=x^2+2px+p+2 \quad だから \ \ R(x)=0\ が実数解をもたない条件は$

$\cfrac{D}{4}=p^2-(p+2)<0$

$(p+1)(p-2)<0$

$\therefore \ \ -1 < p < 2$

$このとき、 A(x)=0,\ \ B(x)=0\ \ が共通の解 \ \alpha \ をもつとすると$

$A(\alpha)=B(\alpha)=0 \quad だから(2)より \quad R(\alpha)=S(\alpha)=0$

$(1)より \quad R(x)=x^2+2px+p+2,\quad S(x)=(-p+1)x-2p+q \quad だから$

\[ \hspace{1em} \left\{ \begin{array}{l} R(\alpha)=\alpha^2+2p\alpha + p+2=0 \hspace{6em}①\\ S(\alpha)=(-p+1)\alpha -2p+q =0 \hspace{5em}②\\ \end{array} \right. \]
$②より \quad (-p+1)\alpha =2p-q \quad において \ \ \alpha \ は虚数だから左辺は虚数、右辺は実数$

$したがって \quad -p+1=0 ,\quad 2p-q=0$

$\therefore \ \ p=1,\ \ q=2　\quad 確かに \ p\ は \ \ -1 < p < 2\ \ を満たしている。$

$このとき①は \quad \alpha^2+2\alpha + 3=0 $

$これを解いて \quad \alpha =-1 \pm \sqrt{1^2-3}=-1 \pm \sqrt{2}i \quad となって虚数である。$


ページの先頭へ↑




メインメニュー　に戻る