群馬大学(医学) 2024年　問題1


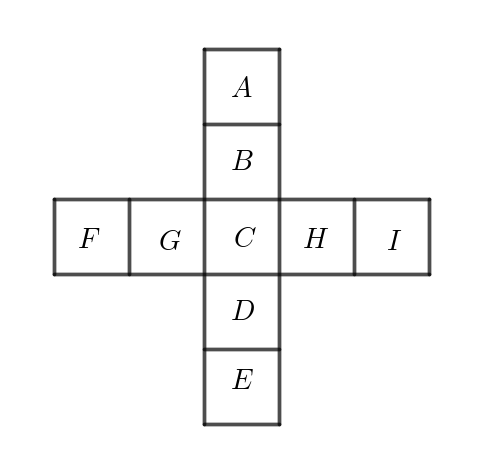
$A\ から \ I\ までの文字が書かれた \ 9\ 枚の同じ大きさの正方形のカードが、右下図のように隙間なく並べられて$
$いる。あるカードの上に置かれた玉 \ Q\ は、1\ 秒ごとに、玉 \ Q\ が置かれているカードに隣\ 接する上下左右の$
$カードのどれかに移動する。n\ は自然数とし、X\ と書かれたカードに置かれた玉 \ Q\ が、n秒後にYと書かれた$
$カードにあるとき、そこまでの経路のの総数を \ N(X,\ Y,\ n)\ で表す。たとえば、N(A,\ B,\ 1)\ は \ 1\ 秒ごとの$
$カード間の移動を→で表すならば、A →Bの経路のみで \ 1\ となり、N(A,\ B,\ 3)\ は、A→B→A→B、$
$A→B→C→B\ の \ 2\ つの経路があるので \ 2\ となる。以下の問に答えよ。$
$\hspace{35em}$ 　
$(1)\ \ n\ は自然数とする。N(C,\ E,\ 2n)\ を求めよ。$
$(2)\ \ n\ は \ 2\ 以上の自然数とする。N(A,\ E,\ 2n)\ を求めよ。$


$(1),(2) は相互に関連しているのでまとめて解く。$

　

(1)


$N(C,\ E,\ 2n)=p_{2n},\quad N(A,\ E,\ 2n)=q_{2n} \ \ とおくと$

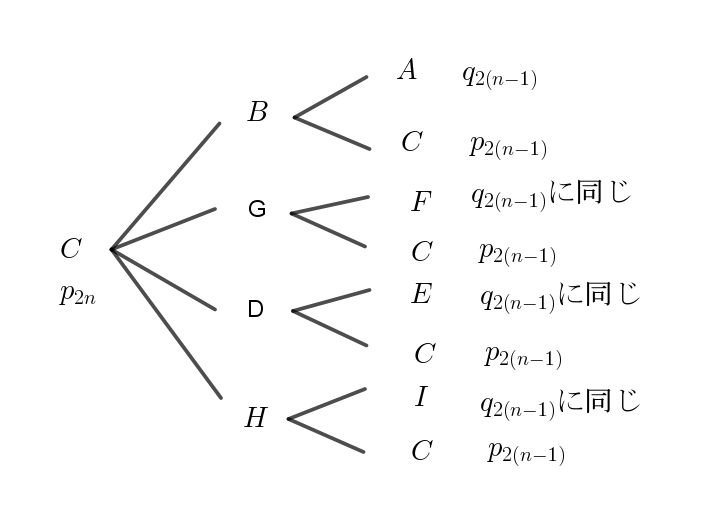
(i)$\ \ カード \ C\ からスタートする \ 2\ 秒後のカード間の移動について$

$右図のような樹形図が得られるが、$

$1\ 秒後には、B,\ G,\ D,\ H \ のいずれかのカードに移動する。$

$〇カード \ B\ に移動すると、2\ 秒後にはカード \ A\ またはカード \ C\ に$

$移動する。$

$\quad ・カード \ A\ に移動すると、A\ からスタートする残り \ 2(n-1)\ 秒での移動となる。$

$\quad ・カード \ C\ に移動すると、また元に戻ったので、残り \ 2(n-1)\ 秒での移動となる。$

$〇カード \ G\ に移動すると、2\ 秒後にはカード \ F\ またはカード \ C\ に移動する。$

$\quad ・カード \ F\ に移動すると、A\ からスタートする残り \ 2(n-1)\ 秒での移動と経路数は同じである。$

$\quad ・カード \ C\ に移動すると、また元に戻ったので、残り \ 2(n-1)\ 秒での移動となる。$

$〇カード \ D,\ \ H\ についても全く同じであるから、次のような漸化式が得られる。$

$\qquad p_{2n}=4(q_{2(n-1)}+p_{2(n-1)} \hspace{5em}① $

　

(ii)$\ \ カード \ A\ からスタートする \ 2\ 秒後のカード間の移動について$

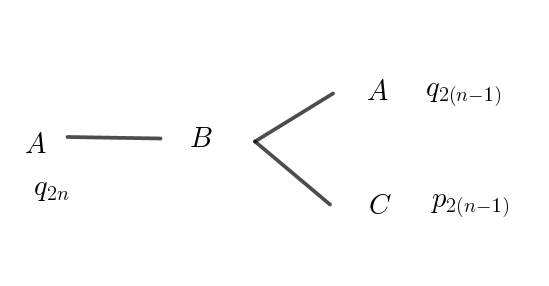
$右図のような樹形図が得られるが、$

$1\ 秒後には、B\ のカードに移動する。$

$2\ 秒後にはカード \ A\ またはカード \ C\ に移動する。$

$\quad ・カード \ A\ に移動すると、また元に戻ったので、残り \ 2(n-1)\ 秒での移動となる。$

$\quad ・カード \ C\ に移動すると、残り \ 2(n-1)\ 秒での \ C\ からの移動となる。$

$次のような漸化式が得られる。$

$\qquad q_{2n}=q_{2(n-1)}+p_{2(n-1)} \hspace{5em}②$

$ただし、p_2=N(C,\ E,\ 2)=1,\quad q_4=N(A,\ E,\ 4)=1 \quad である。$

$簡単のため、2n=m \ \ とおき、p_{2n}=r_m, \quad q_{2n}=s_m \ \ とおくと、r_1=1,\quad s_2=1$

$このとき①、②は$

\[ \hspace{1em} \left\{ \begin{array}{l} r_m=4(s_{m-1} + r_{m-1}) \hspace{5em}③\\ s_m=s_{m-1} + r_{m-1} \hspace{6.3em}④\\ \end{array} \right. \]
$④より \quad r_{m-1}=s_m - s_{m-1} \hspace{5em}⑤$

$⑤を③に代入して$

$s_{m+1} - s_m=4(s_{m-1} + s_m - s_{m-1})$

$s_{m+1} =5s_m$

$s_m=s_2 \cdot 5^{m-2}=5^{m-2}$

$これを⑤に代入して$

$r_m=s_{m+1} - s_m=5^{m-1}-5^{m-2}=(5-1)5^{m-2}=4 \cdot 5^{m-2}$

$p_{2n}=r_n=4 \cdot 5^{n-2}$

$よって \quad N(C,\ E,\ 2n)=4 \cdot 5^{n-2} \quad ただし \ \ N(C,\ E,\ 2)=1$


(2)


$q_{2n}=s_n=5^{n-2}$

$とくに \ \ n=2\ \ のとき \quad 左辺=q_4=1 ,\quad 右辺=5^0=1 \ \ だから \ \ n=2\ のときも成りたつ$

$よって \quad N(A,\ E,\ 2n)=5^{n-2} \ \ (n\ は \ 2\ 以上の自然数)$


ページの先頭へ↑




メインメニュー　に戻る