5 $x^3=2$ のガロア群
(1) 分解体と自己同型写像
$\quad 解は \big(\cfrac{x}{\sqrt[3]{2}}\big)^3=1 より x=\sqrt[3]{2},\ \sqrt[3]{2}\omega,\ \sqrt[3]{2}\omega^2$
$\quad よって分解体は K=Q(\sqrt[3]{2},\ \sqrt[3]{2}\omega,\ \sqrt[3]{2}\omega^2)$
$\quad ところが、\omega=\cfrac{\sqrt[3]{2}\omega^2}{\sqrt[3]{2}\omega} だから \omega \in Q(\sqrt[3]{2},\ \sqrt[3]{2}\omega,\ \sqrt[3]{2}\omega^2)$
$\hspace{2em} \therefore K=Q(\sqrt[3]{2},\omega)$
$\quad Q(\sqrt[3]{2}) \ は \ Q上3次、\ Q(\omega) \ はQ上2次だから \ K=Q(\sqrt[3]{2},\omega) \ は \ Q上 \ 6次 \ である。$
$\quad したがって Qの元は6個の基底を用いて$
$\hspace{3em} \xi=a+b\sqrt[3]{2}+c\sqrt[3]{4}+d\omega + e\sqrt[3]{2}\omega +f\sqrt[3]{4}\omega $
$\quad とおけるから K \ の自己同型写像は6個ある。$
$\quad \sqrt[3]{2} \ の共役元は \sqrt[3]{2}\omega と \sqrt[3]{2}\omega^2 , \hspace{2em} \omega \ の共役元は \omega^2$ だから
(i)$\quad Q(\omega)$ を動かさない同型写像として
$\hspace{3em} \sigma : \sqrt[3]{2} \longrightarrow \sqrt[3]{2}\omega$
があり、
$\hspace{3em} \sigma ^2 : \sqrt[3]{2} \longrightarrow \sqrt[3]{2}\omega \longrightarrow \sqrt[3]{2}\omega ^2$
(ii)$\quad Q(\sqrt[3]{2})$ を動かさない同型写像として
$\hspace{3em} \tau : \omega \longrightarrow \omega ^2$
$\quad があるから$
$\hspace{3em} \tau \sigma \ \ :\ \ \sqrt[3]{2} \xrightarrow {\ \tau \ } \sqrt[3]{2}\omega \xrightarrow{\ \sigma \ } \sqrt[3]{2}\omega , \hspace{1em} \omega \xrightarrow{\ \tau \ } \omega ^2 \xrightarrow{\ \sigma \ } \omega ^2$
$\hspace{3em} \tau \sigma ^2 \ \ :\ \ \sqrt[3]{2} \xrightarrow{\ \tau \ } \sqrt[3]{2} \xrightarrow{\ \sigma ^2 \ } \sqrt[3]{2}\omega ^2 , \hspace{1em} \omega \xrightarrow{\ \tau \ } \omega ^2 \xrightarrow{\ \sigma ^2 \ } \omega ^2$
$\quad これらをまとめると$
$\hspace{3em}$
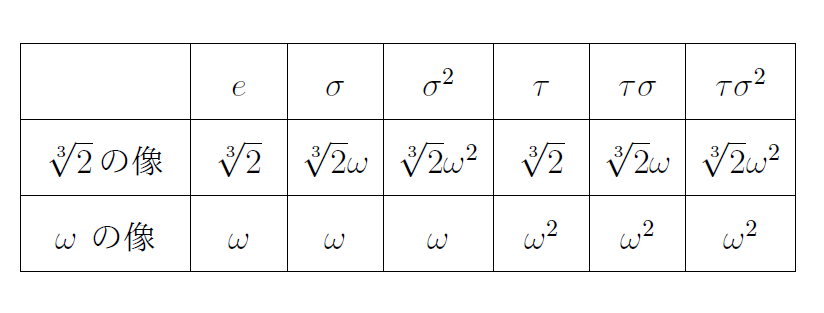
$\quad したがって、ガロア群は \quad G=\{e,\ \sigma , \ \sigma ^2,\ \tau , \ \tau \sigma , \ \tau \sigma ^2 \} $
(2) 不変体
$\quad $ (i) $M_1=\{e,\sigma , \sigma ^2 \} \ の不変体は \ Q(\omega)$
$\quad $ (ii) $M_2=\{e,\tau \}\ については$
\begin{eqnarray*} \xi \tau &=&(a+b\sqrt[3]{2}+c\sqrt[3]{4}+d\omega + e\sqrt[3]{2}\omega +f\sqrt[3]{4}\omega )\tau \hspace{18em}\\ &=&a+b\sqrt[3]{2}+c\sqrt[3]{4}+d\omega ^2 + e\sqrt[3]{2}\omega ^2 +f\sqrt[3]{4}\omega ^2\\ \end{eqnarray*} $\hspace{2em} よって不変体は Q(\sqrt[3]{2})$
$\quad $ (iii) $M_3=\{e,\tau \sigma\}\ については$
$\hspace{5em} \sqrt[3]{2} \xrightarrow{\ \tau \sigma \ } \sqrt[3]{2}\omega \xrightarrow{\ \tau \sigma \ } \sqrt[3]{2}\omega \times \omega ^2 = \sqrt[3]{2}, \hspace{3em} \omega \rightarrow \omega ^2 \rightarrow (\omega ^2)^2=\omega$
$\hspace{2em} よって (\tau \sigma )^2=e だから \ M_3 \ は部分群である。$
\begin{eqnarray*} \xi \tau \sigma &=&(a+b\sqrt[3]{2}+c\sqrt[3]{4}+d\omega + e\sqrt[3]{2}\omega +f\sqrt[3]{4}\omega )\tau \sigma \hspace{17em}\\ &=&a+b\sqrt[3]{2}\omega +c\sqrt[3]{4}\omega ^2 +d\omega ^2 + e\sqrt[3]{2} +f\sqrt[3]{4}\omega \\ \end{eqnarray*} $\hspace{2em} 不変体は Q(\sqrt[3]{4}\omega )$
$\quad $ (iv) $M_4=\{e,\tau \sigma ^2\}\ については$
$\hspace{5em} \sqrt[3]{2} \xrightarrow{\ \tau \sigma ^2 \ } \sqrt[3]{2}\omega ^2 \xrightarrow{\ \tau \sigma ^2 \ } \sqrt[3]{2}\omega ^2 \times (\omega ^2)^2 = \sqrt[3]{2}, \hspace{2em} \omega \rightarrow \omega ^2 \rightarrow (\omega ^2)^2 = \omega $
$\hspace{2em} よって (\tau \sigma ^2 )^2=e だから \ M_4 \ は部分群である。$
\begin{eqnarray*} \xi \tau \sigma^2 &=&(a+b\sqrt[3]{2}+c\sqrt[3]{4}+d\omega + e\sqrt[3]{2}\omega +f\sqrt[3]{4}\omega )\tau \sigma^2 \hspace{15em}\\ &=&a+b\sqrt[3]{2}\omega ^2 +c\sqrt[3]{4}\omega ^4 +d\omega ^2 + e\sqrt[3]{2}\omega ^2 \times \omega ^2+f\sqrt[3]{4}\omega ^4 \times \omega ^2 \hspace{2em}\\ &=&a+b\sqrt[3]{2}\omega ^2+c\sqrt[3]{4}\omega +d\omega ^2 + e\sqrt[3]{2}\omega +f\sqrt[3]{4}\\ \end{eqnarray*} 不変体は $Q(\sqrt[3]{2}\omega )$
(3) 置換による表現
$\hspace{3em} \sqrt[3]{2} \longleftrightarrow 1 , \quad \sqrt[3]{2}\omega \longleftrightarrow 2, \quad \sqrt[3]{2}\omega ^2 \longleftrightarrow 3 $
$\quad のように対応づけると、ガロア群は解の置換そのものであるから$
(i)$\ \sigma \ については$
$\hspace{2em} \sqrt[3]{2}\sigma = \sqrt[3]{2}\omega \qquad \therefore 1 \longrightarrow 2 $
$\hspace{2em} \sqrt[3]{2}\omega \sigma = \sqrt[3]{2}\omega \omega = \sqrt[3]{2}\omega ^2 \quad \therefore 2 \longrightarrow 3 $
$\hspace{2em} \sqrt[3]{2}\omega ^2 \sigma = \sqrt[3]{2}\omega \omega ^2 = \sqrt[3]{2} \quad \therefore 3 \longrightarrow 1 $
$\qquad よって \ \ \sigma= \left( \begin{array}{rr} 1 & 2 & 3 \\ 2 & 3 & 1 \\ \end{array} \right) = \left( \begin{array}{r} 1 & 2 & 3 \\ \end{array} \right)$
$\hspace{3em}\ \ \sigma ^2= \left( \begin{array}{rr} 1 & 2 & 3 \\ 2 & 3 & 1 \\ \end{array} \right) \left( \begin{array}{rr} 1 & 2 & 3 \\ 2 & 3 & 1 \\ \end{array} \right) = \left( \begin{array}{rr} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{array} \right) = \left( \begin{array}{r} 1 & 3 & 2 \\ \end{array} \right)$
(ii)$\ \tau \ については$
$\hspace{2em} \sqrt[3]{2}\tau = \sqrt[3]{2} \qquad \therefore 1 \longrightarrow 1 $
$\hspace{2em} \sqrt[3]{2}\omega \tau = \sqrt[3]{2}\omega ^2 \quad \therefore 2 \longrightarrow 3 $
$\hspace{2em} \sqrt[3]{2}\omega ^2 \tau = \sqrt[3]{2}(\omega ^2)^2 = \sqrt[3]{2}\omega \quad \therefore 3 \longrightarrow 2 $
$\qquad よって \ \ \tau= \left( \begin{array}{rr} 1 & 2 & 3 \\ 1 & 3 & 2 \\ \end{array} \right) = \left( \begin{array}{r} 2 & 3 \\ \end{array} \right)$
(iii)$\ \tau \sigma , \quad \tau \sigma^2 \ については$
$\qquad \ \ \tau \sigma= \left( \begin{array}{rr} 1 & 2 & 3 \\ 1 & 3 & 2 \\ \end{array} \right) \left( \begin{array}{rr} 1 & 2 & 3 \\ 2 & 3 & 1 \\ \end{array} \right) = \left( \begin{array}{rr} 1 & 2 & 3 \\ 2 & 1 & 3 \\ \end{array} \right) = \left( \begin{array}{r} 1 & 2 \\ \end{array} \right)$
$\qquad \ \ \tau \sigma ^2= \left( \begin{array}{rr} 1 & 2 & 3 \\ 1 & 3 & 2 \\ \end{array} \right) \left( \begin{array}{rr} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{array} \right) = \left( \begin{array}{rr} 1 & 2 & 3 \\ 3 & 2 & 1 \\ \end{array} \right) = \left( \begin{array}{r} 1 & 3 \\ \end{array} \right)$
よって、ガロア群は
$\hspace{5em} G=\{e,\ (123),\ (132),\ (23),\ (12),\ (13)\}$
とも表されます。
ガロア群 に戻る
メインメニュー に戻る