福島県立医科大学 2024年　問題4


$xy\ 平面において、点Pは原点を中心とする半径 \ 6\ の円周上を、点Qは原点を中心とする半径 \ 2\ の円周上を$
$それぞれ移動している。時刻 \ t=0\ のとき、P\ は点(6,\ 0)\ に、Qは点(2,\ 0)\ に位置し、それぞれ反時計まわり$
$に一定の速さで連続的に移動する。P\ は \ 4\pi \ 秒で円を \ 1\ 周し、P\ と \ Q\ の移動する速さは等しい。また、線分$
$PQ\ を \ 3:1\ に内分する点を \ R\ とし、t\ 秒時点での \ R\ の座標を \ (f(t),\ g(t)) \ とする。以下の問いに答えよ。$
$(1)\ \ すべての実数 \ t\ \ (t \geqq 0)\ について、f(t)=r(t)\cos t,\ \ g(t)=r(t)\sin t \ \ を満たす関数 \ r(t)\ が存在すること$
$\quad を示せ。$
$(2)\ \ f(t)\ と \ g(t)\ の \ \ 0 \leqq t \leqq \pi \ \ における増減を調べ、最大値と最小値を求めよ。$
$(3)\ \ 媒介変数表示 \ \ x=f(t),\ \ y=g(t) \ \ (0 \leqq t \leqq \pi)\ \ で与えらえる曲線 \ C\ の概形を描け。$
$(4)\ \ (3)の曲線 \ C\ と \ x\ 軸で囲まれた図形の面積を求めよ。$
$(5)\ \ 点Rの軌跡を \ xy\ 平面に描け。$


(1)

　

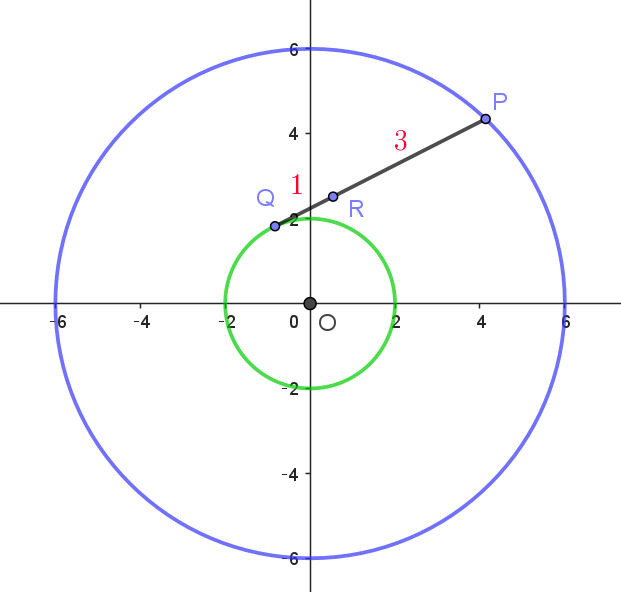
$円運動において、円の半径を\ r、点の動く速さを \ v、周期を \ T、角速度を \ w\ とすると$

$v=rw,\quad w=\cfrac{2\pi}{T} \quad の関係式が成りたつ。$

$点P(x_p,\ y_p) \quad について$

$w_p=\cfrac{2\pi}{4\pi}=\cfrac{1}{2}$

$よって \quad x_p=6\cos \dfrac{t}{2}, \quad y_p=6\sin \dfrac{t}{2}$

$v_p=6w_p=6 \times \cfrac{1}{2}=3$

$点Q(x_q,\ y_q) \quad について$

$P\ と \ Q\ の移動する速さは等しいから \quad v_q=v_p=3$

$よって \quad w_q=\cfrac{v_q}{2}=\cfrac{3}{2}$

$ x_q=2\cos \dfrac{3}{2}t, \quad y_p=2\sin \dfrac{3}{2}t$

$PQ\ を \ 3:1\ に内分する点 \ R(f(t),\ g(t))\ \ は$

\begin{eqnarray*} f(t) &=&\cfrac{1 \times x_p+3\times x_q}{3+1}\\ \\ &=&\cfrac{1}{4} \times 6\cos \dfrac{t}{2}+\cfrac{3}{4} \times 2\cos \dfrac{3}{2}t\\ \\ &=&\cfrac{3}{2}\big(\cos \dfrac{t}{2}+\cos \dfrac{3}{2}t\big)\\ \\ &=&3\cos \dfrac{1}{2}(\dfrac{t}{2}+\dfrac{3t}{2}) \cos \dfrac{1}{2}(\dfrac{t}{2}-\dfrac{3t}{2})\\ \\ &=&3\cos \dfrac{t}{2} \cos t \end{eqnarray*}
\begin{eqnarray*} g(t) &=&\cfrac{1 \times y_p+3\times y_q}{3+1}\\ \\ &=&\cfrac{1}{4} \times 6\sin \dfrac{t}{2}+\cfrac{3}{4} \times 2\sin \dfrac{3}{2}t\\ \\ &=&\cfrac{3}{2}\big(\sin \dfrac{t}{2}+\sin \dfrac{3}{2}t\big)\\ \\ &=&3\sin \dfrac{1}{2}(\dfrac{t}{2}+\dfrac{3t}{2}) \cos \dfrac{1}{2}(\dfrac{t}{2}-\dfrac{3t}{2})\\ \\ &=&3\cos \dfrac{t}{2} \sin t \end{eqnarray*}
$よって \quad r(t)=3\cos \dfrac{t}{2}$


(2)


(i)$\ \ f(t) \quad について$

$f(t)=3\cos \dfrac{t}{2} \cos t=3\cos \dfrac{t}{2} (2\cos^2 \dfrac{t}{2} -1)=6\cos ^3\dfrac{t}{2} -3\cos \dfrac{t}{2} \quad だから$

$f'(t)=9\cos ^2\dfrac{t}{2} (-\sin \dfrac{t}{2}) + \cfrac{3}{2} \sin \dfrac{t}{2}= -9\sin \dfrac{t}{2} (\cos ^2\dfrac{t}{2}- \cfrac{1}{6})= -9\sin \dfrac{t}{2} (\cos \dfrac{t}{2}+ \cfrac{1}{\sqrt{6}})(\cos \dfrac{t}{2}- \cfrac{1}{\sqrt{6}})$

$0 \leqq t \leqq \pi \quad より \quad 　0 \leqq \dfrac{t}{2} \leqq \dfrac{\pi}{2} \quad だから \quad \sin \dfrac{t}{2} \geqq 0, \quad \cos \dfrac{t}{2} \geqq 0 $

$f'(t)=0 \ \ より \ \ \cos \dfrac{t}{2}=\cfrac{1}{\sqrt{6}} \quad これを満たす \ t\ を \ t_0\ とすると \quad \cos \dfrac{t_0}{2}=\cfrac{1}{\sqrt{6}}$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} t & 0 & \cdots & t_0 & \cdots & \pi\\ \hline f'(t) & & - & 0 & + & \\ \hline f(t) & 3 & \searrow & 極小 & \nearrow & 0\\ \end{array} \]
$t=t_0 \ のとき \ f(t)\ は極小かつ最小となり、最小値は \quad f(t_0)=6\big(\cfrac{1}{\sqrt{6}})^3 -3(\cfrac{1}{\sqrt{6}})=\cfrac{1}{\sqrt{6}}-\cfrac{3}{\sqrt{6}}=-\cfrac{\sqrt{6}}{3}$

$f(0)=3,\quad f(\pi)=0 \quad だから \quad t=0 \ のとき \ f(t)\ は最大となり最大値は \ \ 3$


(ii)$\ \ g(t) \quad について$

$g(t)=3\cos \dfrac{t}{2} \sin t=6\cos ^2\dfrac{t}{2}\sin \dfrac{t}{2} =6(1-\sin ^2\dfrac{t}{2})\sin \dfrac{t}{2}=6\sin \dfrac{t}{2} -6\sin^3 \dfrac{t}{2} \quad だから$

$g'(t)=3\cos \dfrac{t}{2} -9\sin ^2 \dfrac{t}{2} \cos \dfrac{t}{2}= -9\cos \dfrac{t}{2} (\sin ^2\dfrac{t}{2}-\cfrac{1}{3})= -9\cos \dfrac{t}{2} (\sin \dfrac{t}{2}+ \cfrac{1}{\sqrt{3}})(\sin \dfrac{t}{2}- \cfrac{1}{\sqrt{3}})$

$g'(t)=0 \ \ より \ \ \sin \dfrac{t}{2}=\cfrac{1}{\sqrt{3}} \quad これを満たす \ t\ を \ t_1\ とすると \quad \sin \dfrac{t_1}{2}=\cfrac{1}{\sqrt{3}}$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} t & 0 & \cdots & t_1 & \cdots & \pi\\ \hline g'(t) & & + & 0 & - & \\ \hline g(t) & 0 & \nearrow & 極大 & \searrow & 0 \\ \end{array} \]
$t=t_1\ のとき \ f(t)\ は極大かつ最大となり、最大値は \ \ g(t_1)=6\big(1-\cfrac{1}{3}) \times \cfrac{1}{\sqrt{3}}=\cfrac{4\sqrt{3}}{3}$

$g(0)=0,\quad g(\pi)=0 \ \ だから \ \ t=0,\ \ \pi \ \ のとき \ g(t)\ は最小となり最小値は \ \ 0$


(3)

　

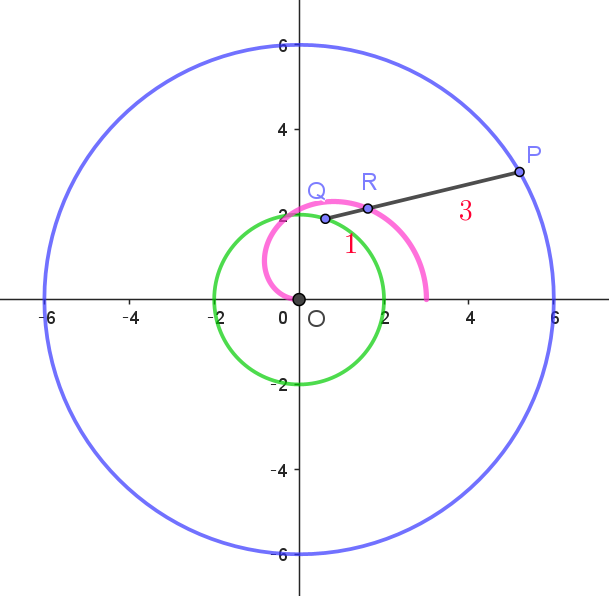
$R(f(t),\ g(t))\ の定義と \ r(t)\ の変化から \ \ 0< t_1 < \dfrac{\pi}{2} < t_0 < \pi \quad である$

$ことがわかる。f(t)\ と \ g(t)\ をまとめた増減表は$
\[ \begin{array}{c||c|c|c|c|c} t & 0 & \cdots & t_1 & \cdots & t_0 & \cdots & \pi\\ \hline f'(t) & & - & - & - & 0 & + & \\ \hline g'(t) & & + & 0 & - & - & - & \\ \hline f(t) & 3 & \leftarrow & \leftarrow & \leftarrow & 極小 & \rightarrow & 0\\ \hline g(t) & 0 & \uparrow & 極大 & \downarrow & \downarrow & \downarrow & 0 \\ \end{array} \]
$曲線 \ C\ の概形は右図のピンク色のグラフのとおり$

$これを拡大したグラフは下図である。$


(4)

　

$S_1,\ \ S_2\ を右図のように定めると$

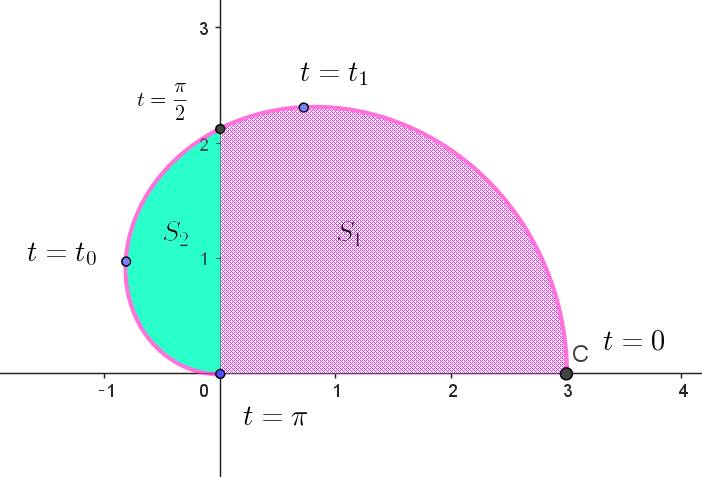
\begin{eqnarray*} S_1 &=&\int_0^3 ydx\\ \\ &=&\int_{\scriptsize{\dfrac{\pi}{2}}}^0 \big(3\cos \dfrac{t}{2} \sin t\big) \big(-9\sin \dfrac{t}{2} (\cos ^2\dfrac{t}{2}- \cfrac{1}{6})\big)dt\\ \\ &=&27\int_0^{\scriptsize{\dfrac{\pi}{2}}} \sin \dfrac{t}{2} \cos \dfrac{t}{2} \sin t \ (\cos ^2\dfrac{t}{2}- \cfrac{1}{6})\big)dt\\ \\ &=&\cfrac{27}{2}\int_0^{\scriptsize{\dfrac{\pi}{2}}} \sin^2 t \big(\cfrac{1+\cos t}{2} - \cfrac{1}{6}\big)dt\\ \\ &=&\cfrac{27}{4}\int_0^{\scriptsize{\dfrac{\pi}{2}}} \sin^2 t \big(\cfrac{2}{3}+\cos t \big)dt\\ \\ &=&\cfrac{9}{2}\int_0^{\scriptsize{\dfrac{\pi}{2}}} \sin^2 t dt + \cfrac{27}{4}\int_0^{\scriptsize{\dfrac{\pi}{2}}} \sin^2 t \cos t dt\\ \\ &=&\cfrac{9}{2}\int_0^{\scriptsize{\dfrac{\pi}{2}}} \dfrac{1}{2}(1-\cos 2t) dt + \cfrac{27}{4}\int_0^{\scriptsize{\dfrac{\pi}{2}}} \sin^2 t \cos t dt\\ \\ &=&\cfrac{9}{4}\big[t- \dfrac{1}{2}\sin 2t \big]_0^{\scriptsize{\dfrac{\pi}{2}}} + \cfrac{27}{4}\big[\dfrac{1}{3}\sin ^3 t\big]_0^{\scriptsize{\dfrac{\pi}{2}}}\\ \\ &=&\dfrac{9}{4} \times \dfrac{\pi}{2} + \dfrac{27}{4} \times \dfrac{1}{3}\\ \\ &=&\cfrac{9}{8}\pi + \cfrac{9}{4} \end{eqnarray*}
\begin{eqnarray*} S_2 &=&\int_0^{\scriptsize{\dfrac{3\sqrt{2}}{2}}} (-x)dy\\ \\ &=&-\int_{\pi}^{\scriptsize{\dfrac{\pi}{2}}} \big(3\cos \dfrac{t}{2} \cos t\big) \big(3\cos \dfrac{t}{2} (1-3\sin^2\dfrac{t}{2}\big)dt\\ \\ &=&9\int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi} \cos ^2\dfrac{t}{2} \cos t \big(1-3\sin ^2\dfrac{t}{2}\big)dt\\ \\ &=&9\int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi} \cos ^2\dfrac{t}{2} \cos t dt -27\int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi}\cos ^2\dfrac{t}{2} \cos t \sin ^2\dfrac{t}{2} dt\\ \\ &=&9\int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi} \dfrac{1}{2}(1+\cos t) \cos t dt -\dfrac{27}{4}\int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi}\sin ^2t \cos t dt\\ \\ &=&\cfrac{9}{2}\int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi} (\cos t +\cos ^2t) dt -\dfrac{27}{4}\int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi}\sin ^2t \cos t dt\\ \\ &=&\cfrac{9}{2}\int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi} (\cos t +\cfrac{1+\cos 2t}{2}) dt -\dfrac{27}{4}\int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi}\sin ^2t \cos t dt\\ \\ &=&\cfrac{9}{2}\big[\sin t + \dfrac{t}{2} +\dfrac{1}{4}\sin 2t\big]_{\scriptsize{\dfrac{\pi}{2}}}^{\pi} -\dfrac{27}{4}\big[\dfrac{1}{3}\sin ^3t\big]_{\scriptsize{\dfrac{\pi}{2}}}^{\pi}\\ \\ &=&\dfrac{9}{2}\big(\cfrac{\pi}{2} -1- \dfrac{\pi}{4}\big)-\dfrac{27}{4} \times \cfrac{1}{3} \times (-1)\\ \\ &=&\cfrac{9}{8}\pi - \cfrac{9}{4} \end{eqnarray*}
$よって \quad S=S_1+S_2=\big(\cfrac{9}{8}\pi + \cfrac{9}{4}\big)+\big(\cfrac{9}{8}\pi - \cfrac{9}{4}\big)=\cfrac{9}{4}\pi $


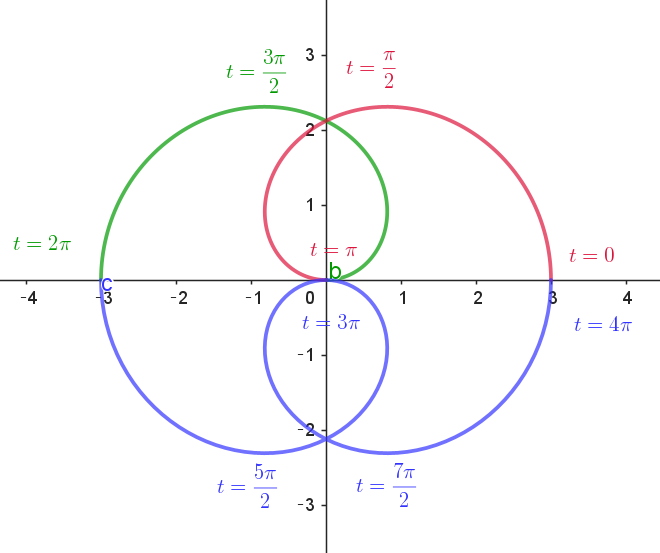
(5)


$R(f(t),\ g(t))\ における \ \ x=3\cos \dfrac{t}{2} \cos t, \quad y=3\cos \dfrac{t}{2} \sin t \ \ は基本周期が \ 4\pi \ の周期関数である。$

$(3)で、0 \leqq t \leqq \pi \ \ の区間におけるグラフをかいてあるので、残りを \ \ \pi \leqq t \leqq 2\pi \ \ と \ \ 2\pi \leqq t \leqq 4\pi \ \ に分けて調べる。$

(i)$\ \ y\ 軸についての対称性$

$曲線 \ C\ 上の点P(x,\ y),\quad x=3\cos \dfrac{t}{2} \cos t,\quad y=3\cos \dfrac{t}{2} \sin t \quad に対して$

$t'=2\pi-t \ \ を満たす \ t'\ をとり \ P'(x',\ y')\ とすると$

　

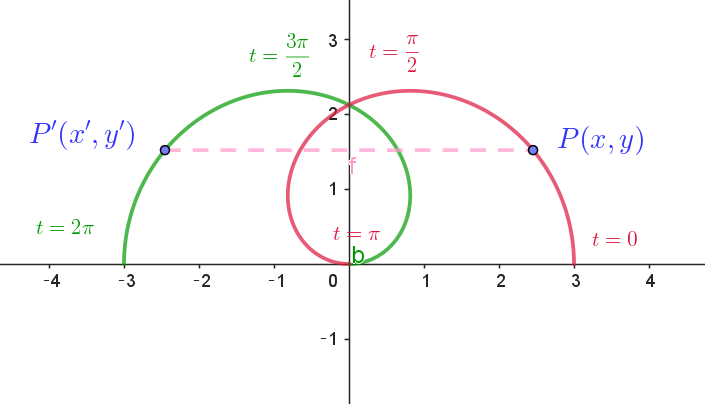
$x'=3\cos \dfrac{t'}{2} \cos t', \quad y'=3\cos \dfrac{t'}{2} \sin t' $

\begin{eqnarray*} x' &=&3\cos \dfrac{2\pi-t}{2} \cos (2\pi-t)\\ \\ &=&3\cos (\pi-\dfrac{t}{2}) \cos (2\pi-t)\\ \\ &=&-3\cos \dfrac{t}{2} \cos t\\ \\ &=&-x \end{eqnarray*}
\begin{eqnarray*} y' &=&3\cos \dfrac{2\pi-t}{2} \sin (2\pi-t)\\ \\ &=&3\cos (\pi-\dfrac{t}{2}) \sin (2\pi-t)\\ \\ &=&-3\cos \dfrac{t}{2} (-\sin t)\\ \\ &=&y \end{eqnarray*}
$したがって \quad 点P'(x',\ y')\ と点P(x,\ y) \ は \ y\ 軸について対称となる。$


(ii)$\ \ x\ 軸についての対称性$

$曲線 \ C\ 上の点P(x,\ y)\quad x=3\cos \dfrac{t}{2} \cos t, \quad y=3\cos \dfrac{t}{2} \sin t \quad に対して$

$t''=4\pi-t \ \ を満たす \ t'' \ をとり \ P''(x'',\ y'')\ とすると$

　

$x''=3\cos \dfrac{t''}{2} \cos t'', \quad y''=3\cos \dfrac{t''}{2} \sin t'' $

\begin{eqnarray*} x'' &=&3\cos \dfrac{4\pi-t}{2} \cos (4\pi-t)\\ \\ &=&3\cos (2\pi-\dfrac{t}{2}) \cos (4\pi-t)\\ \\ &=&3\cos \dfrac{t}{2} \cos t\\ \\ &=&x \end{eqnarray*}
\begin{eqnarray*} y'' &=&3\cos \dfrac{4\pi-t}{2} \sin (4\pi-t)\\ \\ &=&3\cos (2\pi-\dfrac{t}{2}) \sin (4\pi-t)\\ \\ &=&3\cos \dfrac{t}{2} (-\sin t)\\ \\ &=&-y \end{eqnarray*}
$したがって \ \ 点P''(x'',\ y'')\ と点P(x,\ y) \ は \ x\ 軸について対称となる。$

$これらのことに注意して描いた点R\ の軌跡は右図のとおり$


ページの先頭へ↑




メインメニュー　に戻る