複素数平面上の正三角形
$(1)\ \ 積と商の絶対値と偏角$
$\quad 複素数z_1とz_2を極形式で、z_1=r_1(\cos \theta _1+i\sin \theta _1),\quad z_2=r_2(\cos \theta _2+i\sin \theta _2)\quad と表すと$
$\quad z_1z_2=r_1r_2(\cos \theta _1+i\sin \theta _1)(\cos \theta _2+i\sin \theta _2)=r_1r_2\{\cos (\theta _1+\theta _2)+i\sin (\theta _1+\theta _2)\} \quad だから$
$\quad $(i)$\ \ 積$
$\qquad |z_1z_2|=r_1r_2=|z_1||z_2|$
$\qquad z_1z_2の偏角は \ \theta _1+\theta _2 \quad だから \quad \arg z_1z_2=\arg z_1+\arg z_2 $
$\quad $(ii)$\ \ 商$
$\qquad |\cfrac{z_1}{z_2}z_2|=|\cfrac{z_1}{z_2}||z_2| \quad より \quad |z_1|=|\cfrac{z_1}{z_2}||z_2| \quad \therefore \ \ |\cfrac{z_1}{z_2}|=\cfrac{|z_1|}{|z_2|}$
$\qquad \arg \cfrac{z_1}{z_2}z_2=\arg \cfrac{z_1}{z_2}+ \arg z_2 \quad より \quad \arg z_1=\arg \cfrac{z_1}{z_2}+\arg z_2 \quad \therefore \ \ \arg \cfrac{z_1}{z_2}=\arg z_1 - \arg z_2$
$(2)\ \ 2線分のなす角$
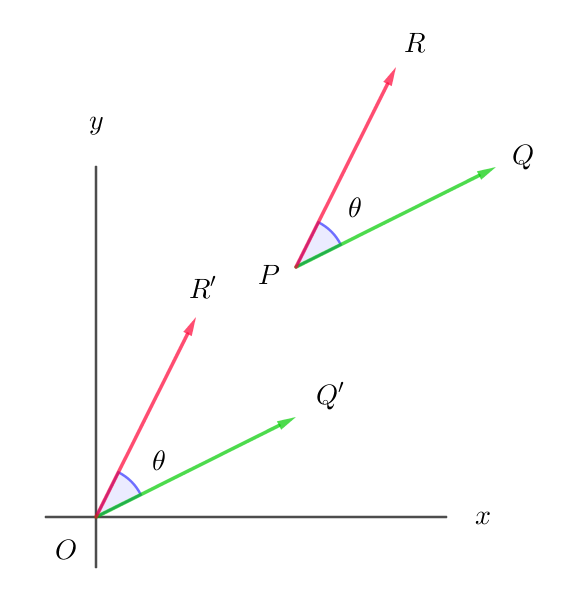
$複素数平面上の異なる3点、P(z_1),\ Q(z_2),\ R(z_3)\ に対して$
$点Pが原点に一致するように平行移動すると$
\begin{eqnarray*}
\theta
&=&\angle QPR\\
&=&\angle Q'OR'\\
&=&\angle xOR' -\angle xOQ'\\
&=&\arg(z_3 - z_1)-\arg(z_2 -z_1)\\
&=&\arg \cfrac{z_3-z_1}{z_2-z_1}
\end{eqnarray*}
$(3)\ \ 正三角形となる条件$
$定理 \quad 複素数平面上の異なる3点、A(\alpha),\ B(\beta),\ C(\gamma)\ でできる三角形ABCが正三角形となる条件は$
$\hspace{6em}\alpha ^2 +\beta ^2 +\gamma ^2 -\alpha \beta -\beta \gamma -\gamma \alpha =0$
$証明$
$\hspace{3em}$
 $\hspace{3em}$
$\hspace{3em}$
$(必要条件)$
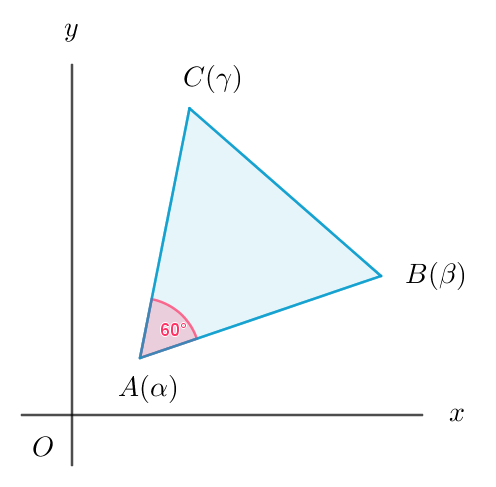
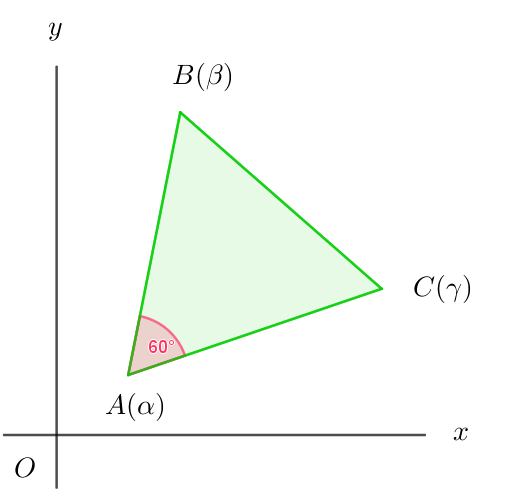
$\qquad 点A(\alpha)を中心に、点B(\beta)を\pm 60°回転した点がC(\gamma)であるから$
$\qquad \cfrac{\gamma - \alpha}{\beta -\alpha}=\cos (\pm 60 °)+i\sin (\pm 60 °)=\cfrac{1 \pm \sqrt{3}i}{2}$
$\qquad 2(\gamma - \alpha)-(\beta -\alpha)=\pm \sqrt{3}i(\beta -\alpha)$
$\qquad 2\gamma - \alpha-\beta =\pm \sqrt{3}i(\beta -\alpha)$
$両辺を平方して$
$\qquad 4\gamma ^2+\alpha ^2+\beta ^2 -4\gamma \alpha +2\alpha \beta -4\beta \gamma =-3(\beta ^2+\alpha ^2 -2\alpha \beta)$
$\qquad \therefore \ \ \alpha ^2 +\beta ^2 +\gamma ^2 -\alpha \beta -\beta \gamma -\gamma \alpha =0$
$(十分条件)$
$\qquad \alpha ^2 +\beta ^2 +\gamma ^2 -\alpha \beta -\beta \gamma -\gamma \alpha =0 \quad より$
$\qquad \gamma ^2 -(\alpha +\beta)\gamma +\alpha \beta =-\alpha ^2 -\beta ^2 +2\alpha \beta $
$\qquad (\gamma -\alpha)(\gamma -\beta)=-(\alpha -\beta)^2$
$\qquad \cfrac{\gamma -\alpha}{\beta -\alpha}=\cfrac{\alpha -\beta}{\gamma -\beta}$
(i)$\ \ 偏角について$
$\qquad \arg \cfrac{\gamma -\alpha}{\beta -\alpha}=\arg \cfrac{\alpha -\beta}{\gamma -\beta}$
$\qquad \therefore \angle BAC=\angle CBA $
$\quad したがって \quad AC=BC \hspace{14em}(1)$
$\qquad \therefore \ \ |\gamma -\alpha|=|\gamma - \beta| \hspace{14em}(2)$
(ii)$\ \ 絶対値について$
$\qquad |\cfrac{\gamma -\alpha}{\beta -\alpha}|=|\cfrac{\alpha -\beta}{\gamma -\beta}|$
$\qquad |\gamma -\alpha||\gamma -\beta |=|\alpha -\beta ||\beta -\alpha |$
$\quad (2)を代入して$
$\qquad |\gamma -\alpha|^2=|\alpha -\beta |^2$
$\qquad \therefore \ \ |\gamma -\alpha |=|\alpha -\beta |$
$\quad よって \quad AC=BA \hspace{15em}(3) $
$(1),(3) より \quad AB=BC=CA \quad となって \quad \triangle ABC \ は正三角形である。$
メインメニュー に戻る