同志社大学(理系) 2025年　問題Ⅲ


$\alpha \ は \ \ 0 < \alpha < \dfrac{\pi}{2} \ \ を満たす定数とし、u=\sin \alpha \ \ とする。関数 \ f(x)=\sin ^2 x +\cos ^2(x+\alpha)\ \ とする。$
$次の問いに答えよ。ただし、必要であれば、次の三角関数の和と積の関係式を用いてよい。$
$\quad \sin(A+B)-\sin(A-B)=2\cos A\sin B,\qquad \cos(A+B)- \cos(A-B)=-2\sin A\sin B$
\[(1)\ \ 定積分 \ \ \int_0^{\scriptsize{\dfrac{\pi}{2}}} f(x)dx \ \ を \ \alpha \ を含まない \ u\ の式で表せ。\] $(2)\ \ 0 \leqq x \leqq \cfrac{\pi}{2} \ \ において、関数 \ f(x) \ は \ x=x_0 \ で最小値 \ c\ をとるとする。このとき、x_0 \ を \ \alpha \ の式で表し、$
$\quad c\ を \ \alpha \ を含まない \ u\ の式で表せ。$
$(3)\ \ (2)の \ c\ について、曲線 \ y=f(x)\ \ (0 \leqq x \leqq \cfrac{\pi}{2})\ \ と \ 3\ つの直線 \ \ y=c,\ \ x=0,\ \ x=\dfrac{\pi}{2}\ \ で囲まれた\ 2\ つの$
$\quad 部分を \ D_1,\ \ D_2 \ とする。D_1,\ \ D_2\ をそれぞれ直線 \ \ y＝c \ の周りに \ 1\ 回転させてできる立体の体積を \ V_1.$
$\quad V_2 \ とするとき、\dfrac{V_1+V_2}{\pi u^2} \ \ を \ \alpha \ を含まない \ u\ の式で表せ。$


(1)


\begin{eqnarray*} & &\int_0^{\scriptsize{\dfrac{\pi}{2}}} f(x)dx\\ \\ &=&\int_0^{\scriptsize{\dfrac{\pi}{2}}} \{\sin ^2 x +\cos ^2(x+\alpha)\}dx\\ \\ &=&\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big\{\dfrac{1}{2}(1-\cos 2x) + \dfrac{1}{2}(1+ \cos (2x+2\alpha)\big\}dx\\ \\ &=&\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big\{1-\dfrac{1}{2}\cos 2x + \dfrac{1}{2} \cos (2x+2\alpha)\big\}dx\\ \\ &=&\big[x-\dfrac{1}{4}\sin 2x + \dfrac{1}{4} \sin (2x+2\alpha)\big]_0^{\scriptsize{\dfrac{\pi}{2}}}\\ \\ &=&\dfrac{\pi}{2} -\dfrac{1}{4}\sin \pi + \dfrac{1}{4} \sin (\pi+2\alpha) -\cfrac{1}{4}\sin 2\alpha \\ \\ &=&\dfrac{\pi}{2} - \dfrac{1}{4} \sin 2\alpha -\cfrac{1}{4}\sin 2\alpha \\ \\ &=&\dfrac{\pi}{2} - \dfrac{1}{2} \sin 2\alpha \\ \\ &=&\dfrac{\pi}{2} - \sin \alpha \ \cos \alpha \\ \\ &=&\dfrac{\pi}{2} - u \sqrt{1-u^2} \\ \end{eqnarray*}

(2)


$f(x)=\sin ^2 x +\cos ^2(x+\alpha)\ \ より$

\begin{eqnarray*} f'(x) &=&2\sin x \cos x -2\cos (x+\alpha) \sin(x+\alpha)\\ \\ &=&\sin 2x - \sin(2x+2\alpha)\\ \\ &=&2\cos(2x+\alpha) \sin(-\alpha)\\ \\ &=&-2\sin \alpha \cos(2x+\alpha)\\ \end{eqnarray*}
$0 < \alpha < \dfrac{\pi}{2},\quad 0 \leqq x \leqq \cfrac{\pi}{2} \ \ より \ \ 0 < 2x + \alpha < \cfrac{3}{2}\pi \ \ だから$

$f'(x)=0 \ の解は \ \ \cos(2x+\alpha)=0\ \ より \ \ 2x + \alpha=\cfrac{\pi}{2} \qquad \therefore \ \ x=\cfrac{\pi}{4}-\cfrac{\alpha}{2}$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & \dfrac{\pi}{4}-\dfrac{\alpha}{2} & \cdots & \dfrac{\pi}{2}\\ \hline f'(x) & & - & 0 & + & \\ \hline f(x) & & \searrow & 極小 & \nearrow & \\ \end{array} \]
$f(x) は\ \ x=\cfrac{\pi}{4}-\cfrac{\alpha}{2} \ \ で極小かつ最小となるから \ \ x_0=\cfrac{\pi}{4}-\cfrac{\alpha}{2}$

$最小値は$
\begin{eqnarray*} c &=&f(\dfrac{\pi}{4}-\dfrac{\alpha}{2})\\ \\ &=&\sin ^2 \big(\dfrac{\pi}{4}-\dfrac{\alpha}{2}\big) + \cos ^2 \big(\dfrac{\pi}{4}+\dfrac{\alpha}{2}\big)\\ \\ &=&\cfrac{1}{2}\big(1-\cos (\dfrac{\pi}{2}-\alpha ) \big) + \cfrac{1}{2}\big(1+ \cos (\dfrac{\pi}{2}+ \alpha )\big)\\ \\ &=&1-\dfrac{1}{2}\sin \alpha - \dfrac{1}{2}\sin \alpha \\ \\ &=&1-\sin \alpha \\ \\ &=&1-u \end{eqnarray*}

(3)

　

\begin{eqnarray*} & &V_1+V_2\\ \\ &=&\pi \int_0^{\scriptsize{\dfrac{\pi}{2}}} (f(x)-c)^2dx\\ \\ &=&\pi \int_0^{\scriptsize{\dfrac{\pi}{2}}} \{\sin ^2 x + \cos ^2(x+\alpha)-c)\}^2dx\\ \\ &=&\pi \int_0^{\scriptsize{\dfrac{\pi}{2}}} \big\{\dfrac{1}{2}(1-\cos 2x) + \dfrac{1}{2}(1+ \cos (2x+2\alpha)-c\big\}^2dx\\ \\ &=&\pi\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big\{1-c-\dfrac{1}{2}\cos 2x + \dfrac{1}{2} \cos (2x+2\alpha)\big\}^2dx\\ \\ &=&\pi\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big\{u+\dfrac{1}{2}(\cos (2x + 2\alpha) - \cos 2x)\big\}^2dx\\ \\ &=&\pi\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big\{u-\sin (2x + \alpha) \sin \alpha \big\}^2dx\\ \\ &=&\pi\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big\{u- u \sin (2x + \alpha) \big\}^2dx\\ \\ &=&\pi u^2\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big(1- \sin (2x + \alpha) \big)^2dx\\ \\ &=&\pi u^2\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big(1- 2\sin (2x + \alpha) + \sin ^2(2x + \alpha) \big)dx\\ \\ &=&\pi u^2\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big(1- 2\sin (2x + \alpha) + \dfrac{1}{2}(1-\cos (4x + 2\alpha) \big)dx\\ \\ &=&\pi u^2\int_0^{\scriptsize{\dfrac{\pi}{2}}} \big(\dfrac{3}{2}- 2\sin (2x + \alpha) - \dfrac{1}{2}\cos (4x + 2\alpha) \big)dx\\ \\ &=&\pi u^2\big[\dfrac{3}{2}x + \cos (2x + \alpha) - \dfrac{1}{8}\sin (4x + 2\alpha) \big]_0^{\scriptsize{\dfrac{\pi}{2}}} \\ \\ &=&\pi u^2\big(\dfrac{3}{2} \times \dfrac{\pi}{2} + \cos (\pi + \alpha) - \dfrac{1}{8}\sin (2\pi + 2\alpha) - \cos \alpha +\dfrac{1}{8}\sin 2\alpha\big)\\ \\ &=&\pi u^2\big(\dfrac{3}{4} \pi - \cos \alpha - \dfrac{1}{8}\sin 2\alpha - \cos \alpha +\dfrac{1}{8}\sin 2\alpha\big)\\ \\ &=&\pi u^2\big(\dfrac{3}{4} \pi - 2\cos \alpha \big)\\ \\ &=&\pi u^2\big(\dfrac{3}{4} \pi - 2\sqrt{1-u^2}\big)\\ \end{eqnarray*}
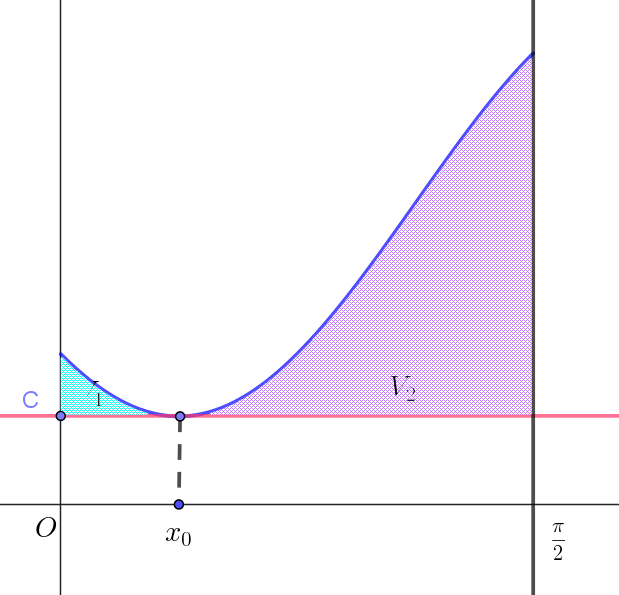
$よって　\cfrac{V_1+V_2}{\pi u^2}=\dfrac{3}{4} \pi - 2\sqrt{1-u^2}$


ページの先頭へ↑



メインメニュー　に戻る