電気通信大学 2024年 問題4
$次の条件によって定められる数列 \ \{a_n\},\ \ \{b_n\}\ を考える。$
$a_1=1,\quad 2na_{n+1}-(n+2)a_n=0 \hspace{6em} ( n=1,\ 2,\ 3,\ \cdots )$
$b_1=1,\quad \dfrac{2n}{n+1}b_{n+1}-\dfrac{n+2}{n+1}b_n=\dfrac{n(n^2-4)}{2^{n-1}} \quad (n=1,\ 2,\ 3,\cdots )$
$このとき、以下の問いに答えよ。$
$(1)\ \ c_n=\dfrac{a_n}{n(n+1)} \ \ とおくとき、c_{n+1}\ を \ c_n\ を用いて表せ。また、数列 \ \{a_n\}\ の一般項を求めよ。$
$(2)\ \ b_2,\ b_3,\ b_4\ を求めよ。$
$(3)\ \ d_n=\dfrac{2^{n-1}}{n(n+1)} b_n \ \ とおくとき、d_{n+1}\ を \ d_n\ を用いて表せ。また数列 \ \{d_n\} \ の一般項を求めよ。$
$(4)\ \ 数列 \ \{b_n\}\ の一般項を求めよ。また、n\ の整式 \ P(n)\ はすべての自然数 \ n\ に対して$
$\qquad b_{n+1}-b_n=\dfrac{P(n)}{2^{n+1}}\ \ をみたす。整式 \ P(n)\ を求めよ。$
$(5)\ \ b_n \ が最大になる自然数 \ n\ を求めよ。$
(1)
$c_n=\dfrac{a_n}{n(n+1)} \quad より \quad a_n=n(n+1)c_n $
$これを \quad 2na_{n+1}-(n+2)a_n=0 \quad に代入して$
$2n(n+1)(n+2)c_{n+1}-(n+2)n(n+1)c_n=0$
$両辺を \ \ 2n(n+1)(n+2) \quad で割って$
$c_{n+1}=\cfrac{1}{2}c_n \quad ただし \quad c_1=\dfrac{a_1}{1 \times 2}=\cfrac{1}{2}$
$c_n=c_1\big(\dfrac{1}{2}\big)^{\scriptsize{n-1}}=\cfrac{1}{2}\big(\dfrac{1}{2}\big)^{\scriptsize{n-1}}=\cfrac{1}{2^n}$
$a_n=n(n+1)c_n=\cfrac{n(n+1)}{2^n}$
$とくに \ \ n=1\ \ とおくと \quad 左辺=a_1=1, \quad 右辺=\cfrac{1 \times 2}{2}=1 $
$よって \ \ すべての自然数 \ n\ に対して \quad a_n=\cfrac{n(n+1)}{2^n}$
(2)
$\dfrac{2n}{n+1}b_{n+1}=\dfrac{n+2}{n+1}b_n+ \cfrac{n(n^2-4)}{2^{n-1}} \quad において$
$n=1 \ \ とおくと \quad \cfrac{2}{2}b_2=\cfrac{3}{2}b_1+ 1 \times (-3) \qquad b_2=\cfrac{3}{2}-3=-\cfrac{3}{2}$
$n=2 \ \ とおくと \quad \cfrac{4}{3}b_3=\cfrac{4}{3}b_2+ \cfrac{2 \times 0}{2} \qquad b_3=b_2=-\cfrac{3}{2}$
$n=3 \ \ とおくと \quad \cfrac{6}{4}b_4=\cfrac{5}{4}b_3+ \cfrac{3 \times 5}{4} \qquad b_4=\cfrac{5}{6}\big(-\cfrac{3}{2}\big)+\cfrac{15}{6}=\cfrac{5}{4}$
(3)
$d_n=\dfrac{2^{n-1}}{n(n+1)} b_n \ \ より \quad b_n=\dfrac{n(n+1)}{2^{n-1}} d_n$
$\dfrac{2n}{n+1}b_{n+1}-\dfrac{n+2}{n+1}b_n=\dfrac{n(n^2-4)}{2^{n-1}} \quad に代入して$
$\dfrac{2n}{n+1} \times \dfrac{(n+1)(n+2)}{2^n}d_{n+1}-\dfrac{n+2}{n+1} \times \dfrac{n(n+1)}{2^{n-1}}d_n=\dfrac{n(n^2-4)}{2^{n-1}}$
$\dfrac{n(n+2)}{2^{n-1}}d_{n+1}- \dfrac{n(n+2)}{2^{n-1}}d_n=\dfrac{n(n^2-4)}{2^{n-1}}$
$d_{n+1}- d_n=n-2$
$ただし \quad d_1=\cfrac{1}{1 \times 2} b_1=\cfrac{1}{2}$
$n \geqq 2 \quad のとき$
\begin{eqnarray*} d_n &=&\cfrac{1}{2}+\sum_{k=1}^{n-1}(k-2)\\ \\ &=&\cfrac{1}{2}+\cfrac{(n-1)n}{2}-2(n-1)\\ \\ &=&\cfrac{1}{2}(n^2-5n+5)\\ \end{eqnarray*} $この式に \ n=1\ を代入すると \quad 右辺=\cfrac{1}{2}(1-5+5)=\cfrac{1}{2}=d_1$
$よって \quad d_n=\cfrac{1}{2}(n^2-5n+5) \qquad (n=1,2,3,\cdots )$
(4)
\begin{eqnarray*} b_n &=&\cfrac{n(n+1)}{2^{n-1}} d_n\\ \\ &=&\cfrac{n(n+1)}{2^{n-1}} \times \cfrac{1}{2}(n^2-5n+5) \\ \\ &=&\cfrac{n(n+1)(n^2-5n+5)}{2^n} \end{eqnarray*} \begin{eqnarray*} P_n &=&2^{n+1}(b_{n+1}-b_n)\\ \\ &=&2^{n+1}\big\{\cfrac{(n+1)(n+2)\big((n+1)^2-5(n+1)+5\big)}{2^{n+1}}-\cfrac{n(n+1)(n^2-5n+5)}{2^n}\big\}\\ \\ &=&(n+1)(n+2)\big((n+1)^2-5(n+1)+5\big)-2n(n+1)(n^2-5n+5) \\ \\ &=&(n+1)\big\{(n+2)(n^2-3n+1)-2n(n^2-5n+5)\big\}\\ \\ &=&(n+1)(-n^3+9n^2-15n+2)\\ \\ &=&-(n+1)(n-2)(n^2-7n+1)\\ \end{eqnarray*}
(5)
$b_{n+1} > b_n \quad ならば \quad P_n > 0 \ \ だから$
$(4)より P_n=-(n+1)(n-2)(n^2-7n+1) > 0$
$よって \quad (n-2)(n^2-7n+1) < 0 \quad である \ n\ を求めればよい。$
$n^2-7n+1=0 \ \ の解は \quad n=\cfrac{7 \pm \sqrt{49-4}}{2}=\cfrac{7 \pm 3\sqrt{5}}{2}$
$\cfrac{7 \pm 3\sqrt{5}}{2}\ \ を自然数でおさえるために$
$f(x)=x^2-7x+1 \ \ のグラフを利用する。$
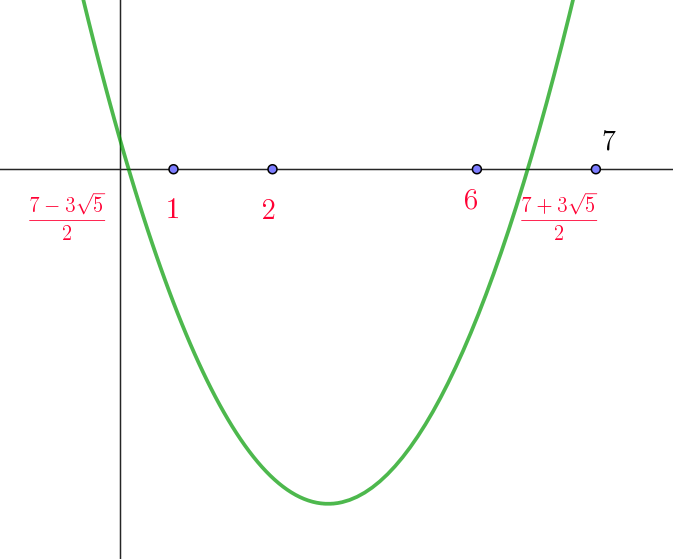
$f(2)=2^2-7 \times 2+1=-9 < 0$
$f(6)=6^2-7 \times 6+1=-5<0$
$f(7)=7^2-7 \times 7+1=1>0$
$したがって、中間値の定理より \quad 0 < \cfrac{7 - 3\sqrt{5}}{2} < 1, \quad 6 < \cfrac{7 + 3\sqrt{5}}{2} < 7 $
$(n-2)(n^2-7n+1) < 0 \ \ の解は \quad n < \cfrac{7 - 3\sqrt{5}}{2}, \quad 2 < n < \cfrac{7 + 3\sqrt{5}}{2}$
$0 < \cfrac{7 - 3\sqrt{5}}{2} < 1 \quad だからこれを満たす自然数 \ n\ はない。$
$2 < n < \cfrac{7 + 3\sqrt{5}}{2}\ \ を満たす自然数 \ n\ は \ \ n=3,\ 4,\ 5,\ 6$
$よって \quad b_3 < b_4 < b_5 < b_6 < b_7 > b_8 > \cdots $
$ゆえに \quad b_n \ が最大となる \ n\ は \quad n=7$
メインメニュー に戻る