電気通信大学 2024年　問題3


$不等式 \ \ x^2+\dfrac{y^2}{4} \leqq 1 \ \ の表す領域を \ D\ とし、楕円 \ \ x^2+\dfrac{y^2}{4} =1\ \ を \ E\ とする。さらに、-1\ と異なる実数 \ a$
$に対して、円\ \ (x-a)^2+y^2=(a+1)^2 \ \ を \ C_a \ とする。このとき、以下の問いに答えよ。$
$(1)\ \ 点P(x,\ y) \ が領域 \ D\ を動くとき、x+\sqrt{2}y \ \ の最大値とそのときの \ x,\ y\ の値を求めよ。$
$(2)\ \ 点P(x,\ y) \ が領域 \ D\ を動くとき、\dfrac{y}{x-3}\ \ の最大値とそのときの \ x,\ y\ の値を求めよ。$
$(3)\ \ 円 \ C_a \ と楕円 \ E\ が点A(-1,\ 0)\ と異なる共有点をもつとき、点 \ A\ と異なる共有点の \ x\ 座標 \ x_0\ を \ a\ の式で$
$\quad 表せ。$
$(4)\ \ 円 \ C_a\ と楕円 \ E\ が点A(-1,\ 0)\ と異なる共有点をもつような \ a\ の値の範囲を求めよ。$


(1)

　

$p:x+\sqrt{2}y=k \quad とおくと$

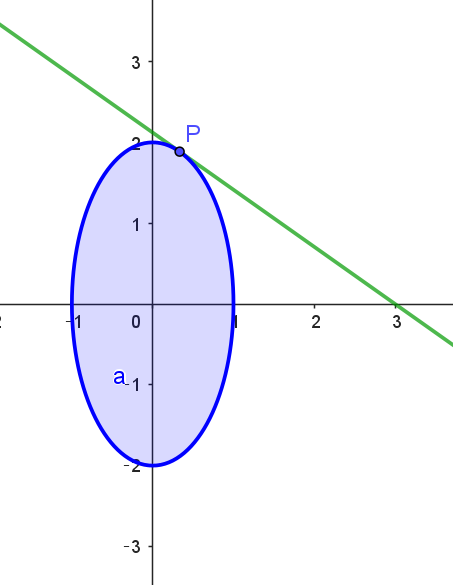
$y=-\cfrac{x}{\sqrt{2}}+\cfrac{k}{\sqrt{2}}$

$点P(x,\ y) \ が領域 \ D\ を動くとき、k=x+\sqrt{2}y \ \ が最大となるのは$

$直線 \ p\ が楕円 \ E\ に接するときだから$

$y=-\cfrac{x}{\sqrt{2}}+\cfrac{k}{\sqrt{2}}\ を \ E\ に代入して$

$x^2+\cfrac{1}{4}\big(-\cfrac{x}{\sqrt{2}}+\cfrac{k}{\sqrt{2}}\big)^2=1$

$x^2+\cfrac{1}{8}(-x+k)^2=1$

$9x^2-2kx+k^2-8=0$

$接する条件は$

$\cfrac{D}{4}=k^2-9(k^2-8)=0$

$k^2=9$

$k=\pm 3$

$よって、最大値は \quad k=x+\sqrt{2}y=3$

$このとき\ \ 重解 \ x\ は \quad x=\cfrac{k}{9}=\cfrac{1}{3}$

$y=-\cfrac{1}{\sqrt{2}} \times \cfrac{1}{3} + \cfrac{1}{\sqrt{2}} \times 3 =\cfrac{4\sqrt{2}}{3}$


$(別解)$

$x+\sqrt{2}y \ \ が最大値をとるのは、領域 \ D\ の周辺、すなわち楕円 \ E\ 上の点(x_0,\ y_0)\ である。$

$したがって、p:x+\sqrt{2}y=k とおくと直線 \ p\ は点(x_0,\ y_0)\ における \ E\ の接線となる。$

$点(x_0,\ y_0)\ における \ E\ の接線は \quad x_0x+\cfrac{y_0y}{4}=1 \quad だからこれが \quad p:x+\sqrt{2}y=k \quad に一致する条件は$

$\cfrac{x_0}{1}=\cfrac{\dfrac{y_0}{4}}{\sqrt{2}}=\cfrac{1}{k}$

$x_0=\cfrac{1}{k},\quad y_0=\cfrac{4\sqrt{2}}{k}$

$(x_0,\ y_0)\ は楕円 \ E\ 上の点だから \quad x_0^2+\cfrac{y_0^2}{4}=1$

$\cfrac{1}{k^2}+\cfrac{8}{k^2}=1$

$\cfrac{9}{k^2}=1$

$k^2=9$

$最大値は \quad k=3$

$このとき \quad x_0=\cfrac{1}{3},\quad y_0=\cfrac{4\sqrt{2}}{3}$


(2)

　

$q:\cfrac{y}{x-3}=m \quad とおくと$

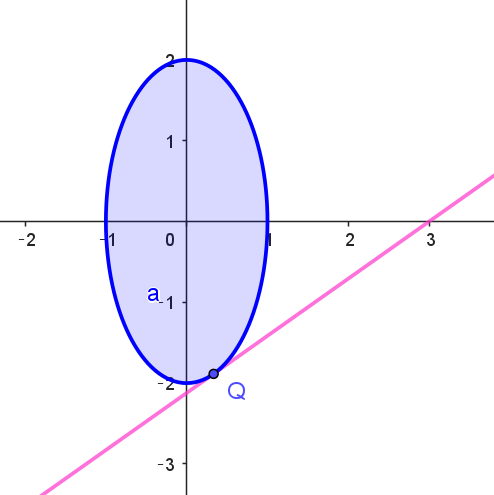
$y=m(x-3) \quad これは点(3,\ 0)\ を通り傾き \ m\ の直線である。$

$点P(x,\ y) \ が領域 \ D\ を動くとき、m\ が最大となるのは$

$直線 q\ が楕円 \ E\ に接するときだから$

$y=m(x-3)\ \ を \ E\ に代入して$

$x^2+\cfrac{m^2}{4}(x-3)^2=1$

$(m^2+4)x^2 -6m^2x+9m^2-4=0$

$接する条件は$

$\cfrac{D}{4}=(3m^2)^2-(m^2+4)(9m^2-4)=0$

$m^2=\cfrac{1}{2}$

$m=\pm \cfrac{1}{\sqrt{2}}$

$最大値は \quad m=\cfrac{y}{x-3}=\cfrac{1}{\sqrt{2}}$

$このとき 重解 \ x\ は \quad x=\cfrac{3m^2}{m^2+4}=\cfrac{3 \times \dfrac{1}{2}}{\dfrac{1}{2}+4}=\cfrac{1}{3}$

$y=\cfrac{1}{\sqrt{2}}(\cfrac{1}{3} -3)=-\cfrac{4\sqrt{2}}{3}$


$(参考)$

$(1)と(2)は \ x\ 軸に関して対称な直線です。$


$(別解)$

$(1)の別解と同様です。$

$q:\cfrac{y}{x-3}=m \quad とおくと \quad mx -y=3m$

$\cfrac{x_0}{m}=\cfrac{\dfrac{y_0}{4}}{-1}=\cfrac{1}{3m}$

$x_0=\cfrac{m}{3m}=\cfrac{1}{3},\quad y_0=-\cfrac{4}{3m}$

$\big(\cfrac{1}{3}\big)^2+\cfrac{1}{4}\big(-\cfrac{4}{3m}\big)^2=1$

$\cfrac{1}{9}+\cfrac{4}{9m^2}=1$

$m^2=\cfrac{1}{2}$

$最大値は \quad m=\cfrac{1}{\sqrt{2}}$

$このとき \quad x_0=\cfrac{1}{3}, \quad y_0=-\cfrac{4\sqrt{2}}{3}$


(3)

　

$(3)\ \ 円 \ C_a \ と楕円 \ E\ の共有点は$

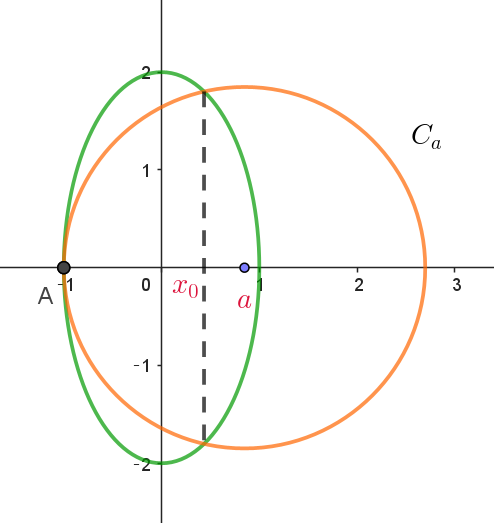
\[ \hspace{1em} \left\{ \begin{array}{l} (x-a)^2+y^2=(a+1)^2 \hspace{5em}①\\ x^2+ \dfrac{y^2}{4}=1 \hspace{10.5em}②\\ \end{array} \right. \]
$②より \quad y^2=4(1-x^2) \quad これを①に代入して$

$(x-a)^2+4(1-x^2)=(a+1)^2$

$3x^2+2ax+2a-3=0$

$(x+1)(3x+2a-3)=0$

$x \ne -1 \ \ だから \quad x=\cfrac{3-2a}{3}$

$したがって \quad x_0=\cfrac{3-2a}{3}$

$ただし \quad \cfrac{3-2a}{3} \ne -1 \quad より \quad a \ne 3$


(4)


$円 \ C_a\ と楕円 \ E\ が点A(-1,\ 0)\ と異なる共有点をもつ条件は$

$-1 < x_0 \leqq 1 \quad だから$

$ -1 <\cfrac{3-2a}{3} \leqq 1$

$-3 < 3-2a \leqq 3$

$-6 < -2a \leqq 0$

$\therefore \ \ 0 \leqq a < 3$


ページの先頭へ↑




メインメニュー　に戻る