電気通信大学 2024年　問題2


$e\ を自然対数の底とし、2\ つの関数$
$\hspace{5em} f(x)=e^x\sqrt{6-e^x} , \quad g(x)=2\sqrt{2}e^{\scriptsize{\dfrac{x}{2}}}$
$を考える。曲線 \ y=f(x)\ を \ C_1,\ 曲線 \ y=g(x)\ を \ C_2\ とする。このとき、以下の問いに答えよ。$
$(1)\ \ 6-e^x \geqq 0 \ \ となる \ x\ の値の範囲は \ \ x \leqq x_0 \ \ である。x_0 \ の値を求めよ。$
$\quad さらに、曲線 \ C_1\ と曲線 \ C_2\ の共有点の座標をすべて求めよ。$
$(2)\ \ 区間 \ \ x < x_0 \ において、導関数 \ f'(x)\ を求め、f(x)\ の極値を求めよ。$
$(3)\ \ 次の不定積分を求めよ。ただし、積分定数は省略してもよい。$
\[\hspace{5em} I=\int e^x\sqrt{6-e^x}dx\] $(4)\ \ 曲線 \ C_1\ と曲線 \ C_2\ で囲まれた領域を \ D\ とする。D\ の面積 \ S\ を求めよ。$
$(5)\ \ D\ を \ x\ 軸のまわりに \ 1\ 回転してできる立体の体積 \ V\ を求めよ。$


(1)


$6-e^x \geqq 0 \quad より \quad e^x \leqq 6 $

$x \leqq \log 6 \quad だから \quad x_0=\log 6$

$曲線 \ C_1\ と曲線 \ C_2\ の共有点の \ x\ 座標はは$

$e^x\sqrt{6-e^x}=2\sqrt{2}e^{\scriptsize{\dfrac{x}{2}}} \quad の解だから両辺平方して$

$e^{2x}(6-e^x)=8e^x$

$e^x(6-e^x)=8$

$e^{2x}-6e^x+8=0$

$(e^x-2)(e^x-4)=0$

$e^x=2 \ \ より \ \ x=\log 2 , \quad f(\log 2)=2 \sqrt{6-2}=4$

$e^x=4 \ \ より \ \ x=\log 4 ,\quad f(\log 4)=4 \sqrt{6-4}=4\sqrt{2}$

$よって、C_1\ とC_2\ の共有点の座標は \quad (\log 2,\ 4)\ と \ (\log 4,\ 4\sqrt{2})$


(2)


$f(x)=e^x\sqrt{6-e^x}$
\begin{eqnarray*} f'(x) &=&e^x\sqrt{6-e^x}+e^x \times \cfrac{-e^x}{2\sqrt{6-e^x}}\\ \\ &=&\cfrac{2e^x(6-e^x)-e^{2x}}{2\sqrt{6-e^x}}\\ \\ &=&\cfrac{e^x(12-2e^x-e^x)}{2\sqrt{6-e^x}}\\ \\ &=&\cfrac{3e^x(4-e^x)}{2\sqrt{6-e^x}}\\ \end{eqnarray*} $f'(x)=0 \quad より \quad 4-e^x=0 \qquad x=\log 4$

$増減表は$
\[ \begin{array}{c||c|c|c|c|c} x & \cdots & \log 4 & \cdots & \log 6\\ \hline f'(x) & + & 0 & - & \\ \hline f(x) & \nearrow & 極大 & \searrow & 0\\ \end{array} \]

　

$f(x) \ は$

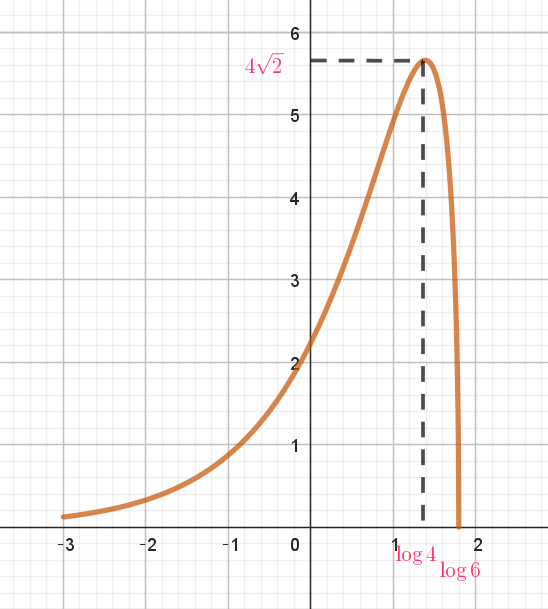
$x=\log 4 \ で 極大値 \quad f(\log 4)=4\sqrt{6-4}=4\sqrt{2}\quad をとる$

$f(\log 6)=0,\quad f(0)=\sqrt{5}$

$x \longrightarrow - \infty \ \ のとき \ \ f(x) \longrightarrow 0$

$y=f(x)\ のグラフは右図のとおりである。$


(3)


\[I=\int e^x\sqrt{6-e^x}dx \quad において \quad e^x=t \quad とおくと \quad e^xdx=dt\] \begin{eqnarray*} I &=&\int \sqrt{6-t}dt\\ \\ &=&-\cfrac{2}{3}(6-t)^{\scriptsize{\dfrac{3}{2}}}\\ \\ &=&-\cfrac{2}{3}(6-e^x)^{\scriptsize{\dfrac{3}{2}}} \end{eqnarray*}

(4)

　

$(2)よりC_1\ とC_2\ の共有点の座標は \ \ x=\log 2 \ \ と \ \ x=\log 4\ \ で$

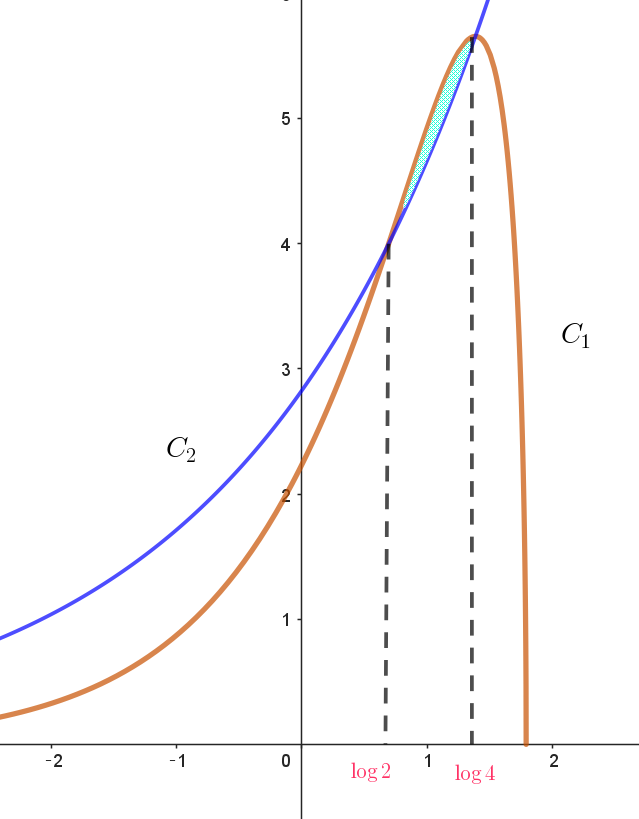
$この区間では \quad f(x) \geqq g(x) \quad だから$
\begin{eqnarray*} S &=&\int_{\log 2}^{\log 4}\big(e^x\sqrt{6-e^x} - 2\sqrt{2}e^{\scriptsize{\dfrac{x}{2}}}\big)dx\\ \\ &=&\big[-\cfrac{2}{3}(6-e^x)^{\scriptsize{\dfrac{3}{2}}} -4\sqrt{2}e^{\scriptsize{\dfrac{x}{2}}}\big]_{\log 2}^{\log 4}\\ \\ &=&-\cfrac{2}{3}\big\{(6-4)^{\scriptsize{\dfrac{3}{2}}}-(6-2)^{\scriptsize{\dfrac{3}{2}}}\big\} -4\sqrt{2}(2 - \sqrt{2})\\ \\ &=&-\cfrac{2}{3}(2\sqrt{2}-8)-8\sqrt{2}+8\\ \\ &=&\cfrac{40-28\sqrt{2}}{3} \end{eqnarray*}

(5)


\begin{eqnarray*} V &=&\pi\int_{\log 2}^{\log 4}f(x)^2dx - \pi\int_{\log 2}^{\log 4} g(x)^2dx\\ \\ &=&\pi\int_{\log 2}^{\log 4} \big\{e^{2x}(6-e^x)-8e^x\big\}dx \\ &=&\pi\int_{\log 2}^{\log 4} (6e^{2x} -e^{3x} -8e^x)dx \\ &=&\pi\big[3e^{2x} -\dfrac{1}{3}e^{3x} -8e^x\big]_{\log 2}^{\log 4}\\ \\ &=&\pi\big(3 \times (4^2 - 2^2) -\dfrac{1}{3}\times (4^3-2^3) -8 \times (4-2)\big)\\ \\ &=&\cfrac{4}{3}\pi \end{eqnarray*}

ページの先頭へ↑




メインメニュー　に戻る