電気通信大学 2024年　問題1


$区間 \ -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\ で定義された関数 \ f(x)=\dfrac{1}{\cos ^2x} - 16\sin ^2x \ \ について、以下の問いに答えよ。$
$(1)\ \ 0 < x < \dfrac{\pi}{2} \ の範囲における \ f(x)=0 \ の解を \ \alpha,\ \beta\ \ (\alpha < \beta ) \ とする。\alpha,\ \beta \ を求めよ。$
$(2)\ \ \tan \alpha,\ \ \tan \beta \ \ の値を求めよ。$
$(3)\ \ 関数 \ f(x)\ の導関数を \ f'(x) \ とする。-\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\ の範囲における \ f'(x)=0\ の解をすべて求めよ。$
$(4)\ \ 区間 \ -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\ において、関数 \ f(x)\ の極値をすべて求めよ。$
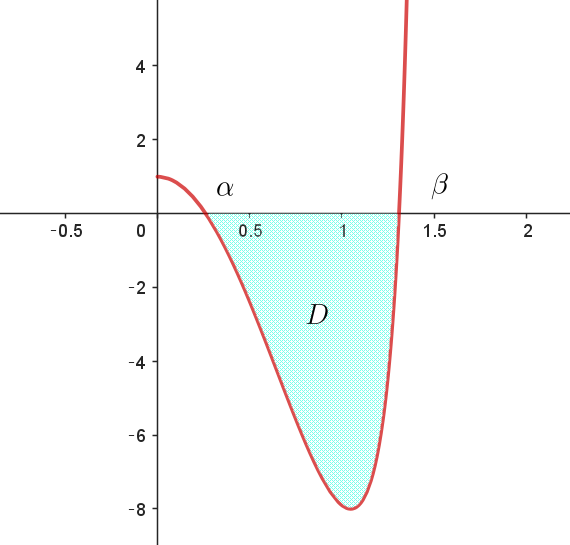
$(5)\ \ 区間 \ 0 < x < \dfrac{\pi}{2}\ において、曲線 \ y=f(x)\ と \ x\ 軸で囲まれた領域を \ D\ とする。D\ の面積 \ S\ を求めよ。$


(1)


$f(x)=\dfrac{1}{\cos ^2x} - 16\sin ^2x =0 \quad より $

$\big(\dfrac{1}{\cos x} + 4\sin x\big) \big(\dfrac{1}{\cos x} - 4\sin x\big)=0$

$0 < x < \dfrac{\pi}{2} \ の範囲においては \ \ \sin x > 0, \ \ \cos x >0 \quad だから$

$\dfrac{1}{\cos x} - 4\sin x =0$

$4\sin x \cos x=1$

$\sin 2x=\cfrac{1}{2}$

$0 < 2x < \pi \quad より \quad 2x=\cfrac{\pi}{6},\quad \cfrac{5}{6}\pi$

$x=\cfrac{\pi}{12},\quad \cfrac{5}{12}\pi$

$したがって \quad \alpha =\cfrac{\pi}{12}, \quad \beta=\cfrac{5}{12}\pi$


(2)


$\tan \alpha=\tan \cfrac{\pi}{12}=\tan (\dfrac{\pi}{3}-\dfrac{\pi}{4}) \quad だから$

$\tan \alpha=\cfrac{\tan \dfrac{\pi}{3}- \tan \dfrac{\pi}{4}}{1+\tan \dfrac{\pi}{3}\tan \dfrac{\pi}{4}}=\cfrac{\sqrt{3}-1}{1+\sqrt{3} \times 1}=\cfrac{(\sqrt{3}-1)^2}{2}=2-\sqrt{3}$

$\tan \beta=\tan \cfrac{5}{12}\pi=\tan (\dfrac{\pi}{6}+\dfrac{\pi}{4}) \quad だから$

$\tan \beta=\cfrac{\tan \dfrac{\pi}{6}+ \tan \dfrac{\pi}{4}}{1-\tan \dfrac{\pi}{6}\tan \dfrac{\pi}{4}}=\cfrac{\dfrac{1}{\sqrt{3}}+1}{1-\dfrac{1}{\sqrt{3}} \times 1}=\cfrac{\sqrt{3}+1}{\sqrt{3}-1}=\cfrac{(\sqrt{3}+!)^2}{2}=2+\sqrt{3}$


(3)


$f(x)=\dfrac{1}{\cos ^2x} - 16\sin ^2x =0 \quad より $

\begin{eqnarray*} f'(x) &=&-\cfrac{2\cos x(-\sin x)}{\cos ^4 x}-32\sin x\cos x \\ \\ &=&\cfrac{2\sin x}{\cos ^3x}-32\sin x\cos x\\ \\ &=&\cfrac{2\sin x(1-16\cos ^4x)}{\cos ^3x}\\ \\ &=&\cfrac{2\sin x(1-2\cos x)(1+2\cos x)(1+4\cos ^2x)}{\cos ^3x}\\ \end{eqnarray*}
$-\dfrac{\pi}{2} < x < \dfrac{\pi}{2}\ \ の範囲における \ f'(x)=0\ の解は$

$\sin x=0 \ \ より \ \ x=0 \ \ と \ \ \cos x=\cfrac{1}{2} \ \ より \ \ x=\pm \cfrac{\pi}{3}$


(4)


$f(x)\ は偶関数だから対称性から \ \ 0 \leqq x < \cfrac{\pi}{2}\ \ で調べればよい。増減表は$
\[ \begin{array}{c||c|c|c|c|c} x & 0 & \cdots & \dfrac{\pi}{3} & \cdots & \dfrac{\pi}{2}\\ \hline f'(x) & 0 & - & 0 & + \\ \hline f(x) & 極大 & \searrow & 極小 & \nearrow \\ \end{array} \]

　

$f(x) \ は$

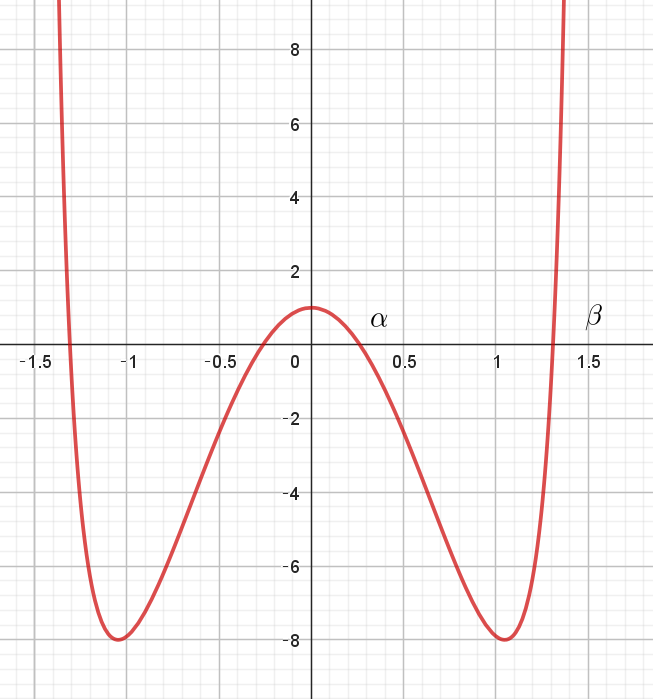
$x=0 \ で 極大値 \quad f(0)=1$

$x=\pm \cfrac{\pi}{3} で極小値 \quad f(\dfrac{\pi}{3})=\cfrac{1}{\cos ^2\dfrac{\pi}{3}}-16\sin ^2\dfrac{\pi}{3}=4-16 \times \cfrac{3}{4}=-8$

$なお、x \longrightarrow \pm \cfrac{\pi}{2} \ \ のとき \ \ f(x) \longrightarrow +\infty$

$y=f(x)\ のグラフは右図のとおりである。$


(5)

　

\begin{eqnarray*} S &=&-\int_{\alpha}^{\beta}f(x)dx\\ \\ &=&-\int_{\alpha}^{\beta}\big(\dfrac{1}{\cos ^2x} - 16\sin ^2x \big)dx\\ \\ &=&-\int_{\alpha}^{\beta}\big(\dfrac{1}{\cos ^2x} - 8(1-\cos 2x) \big)dx\\ \\ &=&-\big[\tan x - 8(x-\dfrac{1}{2}\sin 2x) \big]_{\alpha}^{\beta}\\ \\ &=&-(\tan \beta -\tan \alpha) + 8(\beta -\alpha) -4 (\sin 2\beta - \sin 2\alpha)\\ \\ &=&-(2+\sqrt{3})+(2-\sqrt{3})+8\big(\dfrac{5}{12}\pi-\dfrac{\pi}{12}\big)-4\big(\sin \dfrac{5}{6}\pi- \sin \dfrac{\pi}{6}\big)\\ \\ &=&-2\sqrt{3} +8 \times \dfrac{\pi}{3} -4\big(\dfrac{1}{2}- \dfrac{1}{2}\big)\\ \\ &=&\dfrac{8}{3}\pi -2\sqrt{3} \end{eqnarray*}

ページの先頭へ↑




メインメニュー　に戻る