3次方程式の実数解を求める方法
1 3次方程式の変形
$3次方程式 x^3+px^2+qx+r=0 に対して x=y-\cfrac{p}{3} とおくと$
$y^3+\big(q-\cfrac{p^2}{3}\big)y+r-\cfrac{pq}{3}+\cfrac{2}{27}p^3=0 となるから y^3+ay=b とおける。$
$y=2\sqrt{\cfrac{|a|}{3}}\ z とおくと 8\cfrac{|a|}{3}\sqrt{\cfrac{|a|}{3}}z^3+2a\sqrt{\cfrac{|a|}{3}}\ z=b$
$\therefore \ 4z^3+3\cfrac{a}{|a|} z =\cfrac{b}{2\cfrac{|a|}{3}\sqrt{\cfrac{|a|}{3}}}$
$よって、一般に3次方程式は 4z^3 \pm 3z =c と変形できることがわかりました。$
$zの係数の符号とcの値で4通りに分けて考察します。$
2 $4z^3 - 3z =c$ の解
$w=4z^3-3z のグラフは$
$\quad z=\cfrac{1}{2} で極小値 -1$
$\quad z=-\cfrac{1}{2} で極大値 1$
$\quad z=1 \ \ のとき\ \ w=1$
$\quad z=-1 \ \ のとき w=-1$
$4z^3 - 3z =c の解はグラフの交点を調べて$
$\quad c= 1 \ \ のときは z=1,\ \ -\cfrac{1}{2}(重解)$
$\quad c= -1 \ \ のときは z=-1,\ \ \cfrac{1}{2}(重解)$
$とすぐに求まるから今後は c \neq \pm 1 とする。$
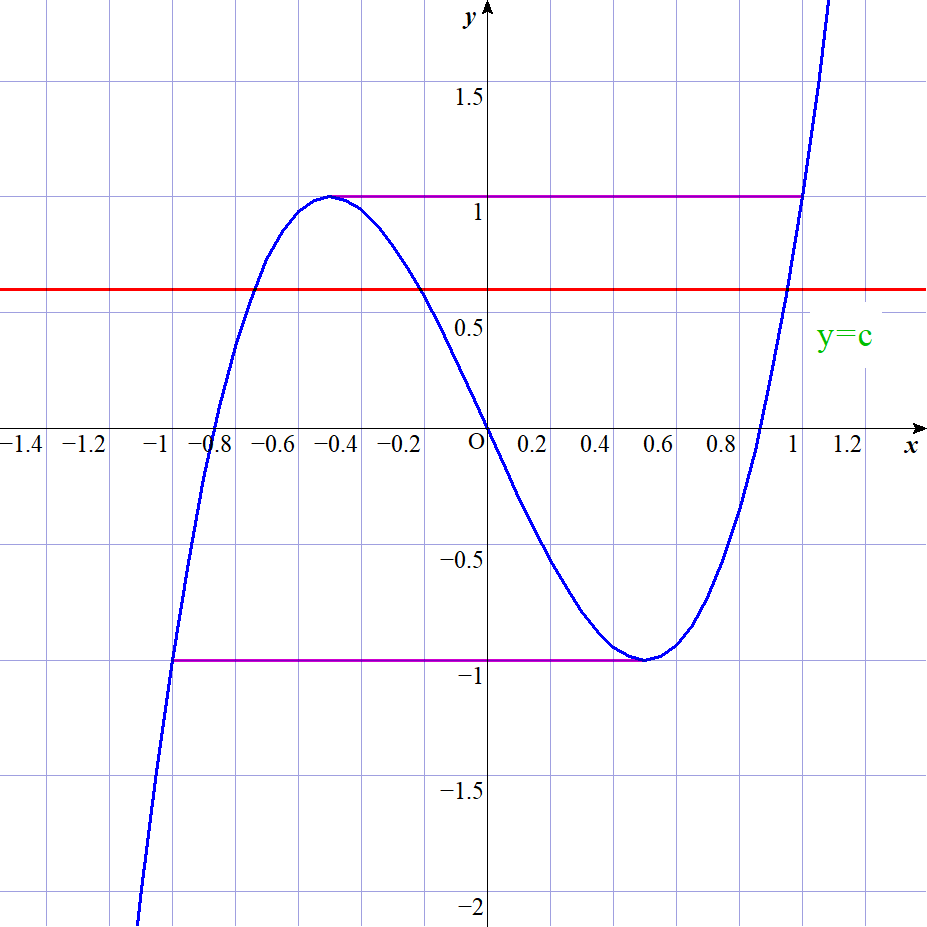
$(1)\ \ -1 < c < 1 のとき$
$w=4z^3-3z \ と\ w=c\ のグラフは上図(座標軸はx,yとなっていますが)のとおりで、異なる3点で$
$交わるから、4z^3 -3z=c は3つの実数解 \ \alpha , \beta , \gamma をもち$
$\qquad \cfrac{1}{2} < \alpha < 1,\ \ -\cfrac{1}{2} < \beta < \cfrac{1}{2},\ \ -1 < \gamma < -\cfrac{1}{2} $
(i)$\ \ \cfrac{1}{2} < \alpha < 1 より \alpha =\cos \theta \ \ を満たす\theta が\ \ 0 < \theta < \cfrac{\pi}{3} \ \ に存在する。$
$\quad 4\cos ^3 \theta -3\cos \theta =c より \cos 3\theta =c$
$\quad 0 < 3\theta <\pi \ \ だから 3\theta =\cos ^{-1}c \quad \theta=\cfrac{1}{3}\cos ^{-1}c \ \ \therefore \alpha =\cos \big(\cfrac{1}{3}\cos ^{-1}c\big) $
(ii)$\ \ \cos (3\theta +2\pi)=\cos 3\theta だから \cos 3(\theta +\cfrac{2\pi}{3})=c$
$\qquad \theta '=\theta +\cfrac{2\pi}{3} とおくと \cos 3\theta' =c だから \cos \theta '=\cos \big(\theta +\cfrac{2\pi}{3}\big) \ \ も解である。$
$\qquad 0 < \theta < \cfrac{\pi}{3} だから \cfrac{2\pi}{3} < \theta +\cfrac{2\pi}{3} < \pi$
$\qquad よって \cos \theta ' < 0 となり \gamma =\cos \theta '=\cos (\theta +\cfrac{2\pi}{3})=\cos \big(\cfrac{1}{3}\cos ^{-1}c +\cfrac{2\pi}{3}\big) $
(iii)$\ \ \cos (3\theta +4\pi)=\cos 3\theta だから \cos 3(\theta +\cfrac{4\pi}{3})=c$
$\qquad \theta ''=\theta +\cfrac{4\pi}{3} とおくと \cos 3\theta''=c だから \cos \theta '' =\cos \big(\theta +\cfrac{4\pi}{3}\big) \ も解である。$
$\qquad 0 < \theta < \cfrac{\pi}{3} だから \cfrac{4\pi}{3} < \theta +\cfrac{4\pi}{3} < \cfrac{5\pi}{3}$
$\qquad したがって \cos \theta '' \ \ は正にも負にもなりうるから$
$\qquad \beta =\cos \theta''=\cos \big(\theta +\cfrac{4\pi}{3}\big)=\cos \big(\cfrac{1}{3}\cos ^{-1}c +\cfrac{4\pi}{3}\big) $
(i),(ii),(iii)$より 4z^3 -3z=c の解は$
$\alpha =\cos \big(\cfrac{1}{3}\cos ^{-1}c \big) ,\quad \gamma =\cos \big(\cfrac{1}{3}\cos ^{-1}c+\cfrac{2}{3}\pi\big), \quad \beta =\cos \big(\cfrac{1}{3}\cos ^{-1}c+\cfrac{4}{3}\pi\big)$
$(2)\ \ c > 1 のとき$
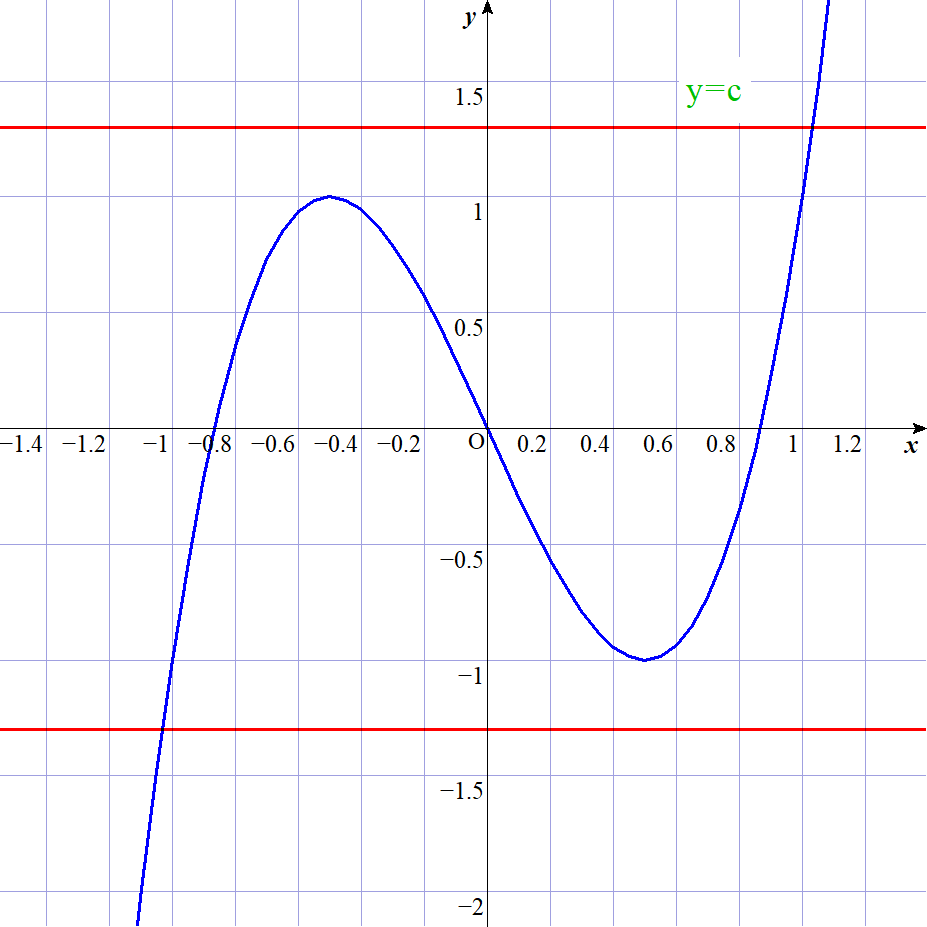
$実数解 \alpha をもつ。$
$明らかに \alpha > 1 \ \ だから \alpha =\cos \theta \ \ とは$
$置けません。ではどうするか$
$\cos 3\theta =4\cos ^3 \theta -3\cos \theta に類似した性質を$
$もった公式を探すと、双曲線関数の$
$\qquad \cosh x= \cfrac{e^x + e^{-x}}{2}$
$があります。$
$ \cosh x \geqq 1 \ \ で \cosh 3x = 4\cosh ^3x - 3\cosh x$
$を満たします。$
$詳しくは $ 双曲線関数$を参考にしてください。$
$そこで z=\cosh \theta とおくと$
$\cosh 3\theta =c より \theta=\cfrac{1}{3}\cosh ^{-1}c$
$z=\cosh \big(\cfrac{1}{3}\cosh ^{-1}c \big) と求まります。$
$(3)\ \ c < -1 のとき$
$4z^3-3z=c は 4(-z)^3-3(-z)=-c とすると -c > 1 だから (2)がつかえて$
$-z=\cosh \theta とおくと$
$4\cosh ^3\theta -3\cosh \theta =-c \quad \cosh 3\theta =-c より \theta =\cfrac{1}{3}\cosh ^{-1}(-c)$
$z=-\cosh \big(\cfrac{1}{3}\cosh ^{-1}(-c) \big) と求まります。$
3 $4z^3 + 3z =c$ の解
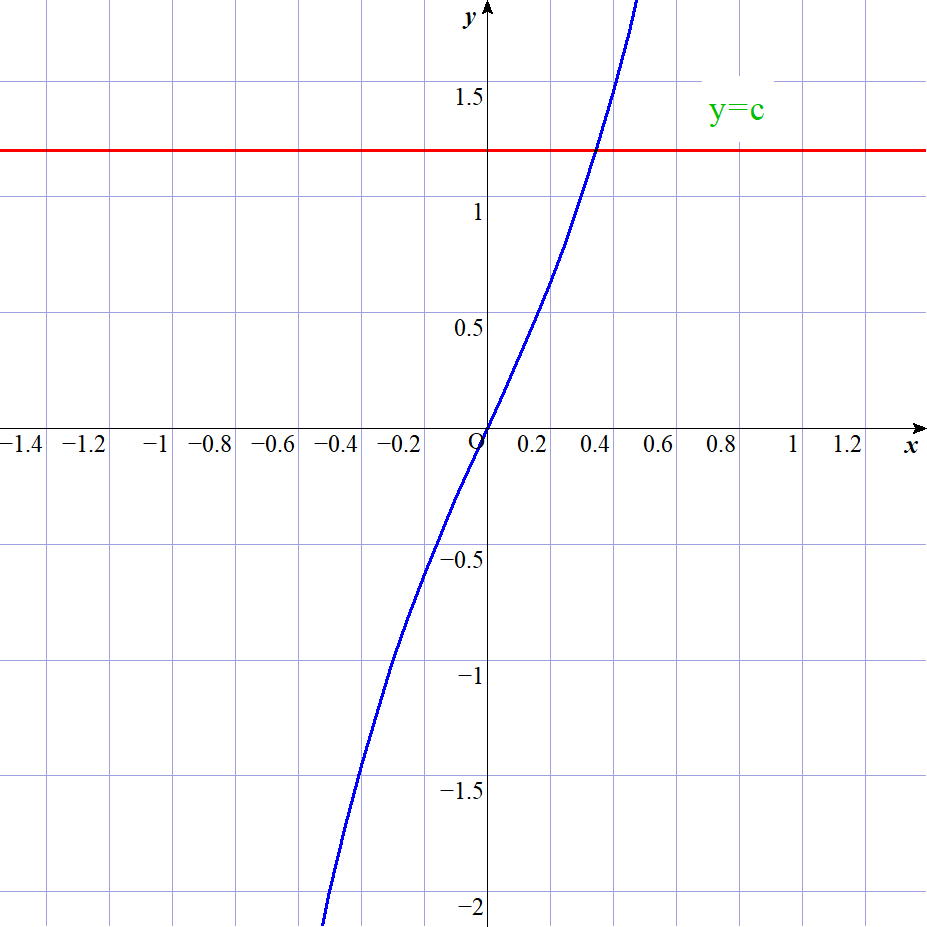
$単調増加、したがって$
$4z^3+3z=c はただ1つの実数解をもつ。$
$z=\sinh \theta とおくと -\infty < z < \infty であり$
$4\sinh ^3 \theta + 3\sinh \theta =c となって$
$\sinh 3\theta =c より \theta=\cfrac{1}{3}\sinh ^{-1}c$
$よって$
$z=\sinh \big(\cfrac{1}{3}\sinh ^{-1}c \big)$
$以上で3次方程式の実数解を求めることができました。$
$まとめてみましょう。$
$\quad 1\quad 4z^3 - 3z =c の解は$
$\qquad (1)\ \ -1 < c < 1 のとき$
$\hspace{5em} \alpha =\cos \big(\cfrac{1}{3}\cos ^{-1}c \big),
\quad \gamma=\cos \big(\cfrac{1}{3}\cos ^{-1}c+\cfrac{2}{3}\pi\big),
\quad \beta=\cos \big(\cfrac{1}{3}\cos ^{-1}c+\cfrac{4}{3}\pi\big)$
$\qquad (2)\ \ c > 1 のとき$
$\hspace{5em} z=\cosh \big(\cfrac{1}{3}\cosh ^{-1}c \big)$
$\qquad (3)\ \ c < -1 のとき$
$\hspace{5em} z=-\cosh \big(\cfrac{1}{3}\cosh ^{-1}(-c) \big)$
$\quad 2\quad 4z^3 + 3z =c の解は$
$\hspace{5em} z=\sinh \big(\cfrac{1}{3}\sinh ^{-1}c \big)$
4 具体的な問題を解いてみましょう。
$例1\quad 3x^3-x=\cfrac{1}{9}$
$\quad 両辺を3で割って x^3-\cfrac{1}{3}x=\cfrac{1}{27}$
$\quad x=2\sqrt{\cfrac{1}{3}\times \cfrac{1}{3}}\ y=\cfrac{2}{3}y とおくと \cfrac{8}{27}y^3-\cfrac{2}{9}y=\cfrac{1}{27}$
$\quad \therefore 4y^3-3y=\cfrac{1}{2}$
$\qquad \alpha =\cos \big(\cfrac{1}{3}\cos ^{-1}\cfrac{1}{2}\big)=\cos \big(\cfrac{1}{3} \times \cfrac{\pi}{3}\big)=\cos \cfrac{\pi}{9}$
$\qquad \gamma =\cos \big(\cfrac{1}{9}\pi+\cfrac{2}{3}\pi\big)=\cos \cfrac{7}{9}\pi=-\cos \cfrac{2\pi}{9}$
$\qquad \beta =\cos \big(\cfrac{1}{9}\pi+\cfrac{4}{3}\pi\big)=\cos \cfrac{13}{9}\pi=-\cos \cfrac{4\pi}{9}$
$したがって$
$\qquad x_1=\cfrac{2}{3}\cos \cfrac{\pi}{9} = 0.62646,\quad x_2=-\cfrac{2}{3}\cos \cfrac{2\pi}{9} = -0.51070,\quad x_3=-\cfrac{2}{3}\cos \cfrac{4\pi}{9} = -0.11577$
$例2 \quad x^3+3x^2+2=0$
$x=y-1 とおくと (y-1)^3+3(y-1)^2+2=0 \hspace{3em} \therefore y^3-3y=-4$
$y=2z とおくと 4z^3-3z=-2 \hspace{3em} 4(-z)^3-3(-z)=2$
$-z=\cosh \theta とおくと \cosh 3\theta =2 \hspace{3em} \theta=\cfrac{1}{3}\cosh ^{-1} 2$
$\quad z=-\cosh \big(\cfrac{1}{3}\cosh^{-1}2\big) = -\cosh (\cfrac{1}{3}\times 1.31696)=-\cosh 0.43899 =-1.09791$
$\quad y=2 \times (-1.09791)=-2.19582$
$\quad x=-2.19582 -1=-3.19582$
$例3 \quad x^3-3x^2+6x-7=0$
$x=y+1 とおくと (y+1)^3-3(y+1)^2+6(y+1)-7=0 \hspace{3em} y^3+3y=3$
$y=2z とおくと 4z^3+3z=\cfrac{3}{2} $
$\quad z=\sinh \big(\cfrac{1}{3}\sinh ^{-1} \cfrac{3}{2}\big)=\sinh \big(\cfrac{1}{3} \times 1.19476\big)=\sinh 0.39825=0.40887$
$\quad y=2 \times 0.40887=0.81774$
$\quad x=0.81774 +1=1.81774$
メインメニュー に戻る