3 自由度nのχ2乗分布
$n個の確率変数X_1,X_2,\cdots , X_nが互いに独立に標準正規分布N(0,1)にしたがうとき$
$Y=X_1^2+X_2^2+\cdots +X_n^2 \quad で定まる確率変数Yの確率密度関数を求めましょう。$
$1\ \ と\ \ 2 \ \ より、f_k(y)=C_k \ y^{\small{\dfrac{k-2}{2}}}e^{\small{-\dfrac{y}{2}}} \quad (C_k は定数) \ と考えられるのでこれを数学的帰納法で証明しましょう。$
(i)$\ k=1 のとき C_1=\cfrac{1}{\sqrt{2\pi}} です。$
(ii)$\ k=n-1 \ \ のとき成りたつとすると$
$\qquad Y=\underbrace{(X_1^2+X_2^2+\cdots +X_{n-1}^2)}_{\substack{\large Y_{n-1}}}+\underbrace{X_n^2}_{\substack{\large Y_1}} $
$と考えて、合成積を用いると$
\begin{eqnarray*} f_n(x) &=&\int _0^x f_{n-1}(y)f_1(x-y)dy\\ &=&\int _0^x C_{n-1} y^{\small{\dfrac{n-3}{2}}} e^{\small{-\dfrac{y}{2}}} \times C_1(x-y)^{\small{-\dfrac{1}{2}}}e^{\small{-\dfrac{x-y}{2}}}dy\\ &=&C_1C_{n-1} e^{\small{-\dfrac{x}{2}}} \int _0^x y^{\small{\dfrac{n-3}{2}}} (x-y)^{\small{-\dfrac{1}{2}}}dy\\ \end{eqnarray*} $y=xu \ \ と変数変換すると dy=xdu $
\begin{eqnarray*} f_n(x) &=&C_1C_{n-1} e^{\small{-\dfrac{x}{2}}} \int _0^1 (xu)^{\small{\dfrac{n-3}{2}}} (x-xu)^{\small{-\dfrac{1}{2}}} \ xdu\\ \\ &=&C_1C_{n-1} x^{\small{\dfrac{n-3}{2}-\dfrac{1}{2}}+\large{1}} \ e^{\small{-\dfrac{x}{2}}} \int _0^1 u^{\small{\dfrac{n-3}{2}}} (1-u)^{\small{-\dfrac{1}{2}}}du\\ \\ &=&C_1C_{n-1} x^{\small{\dfrac{n-2}{2}}} e^{\small{-\dfrac{x}{2}}}\int _0^1 u^{\small{\dfrac{n-3}{2}}} (1-u)^{\small{-\dfrac{1}{2}}}du\\ \end{eqnarray*} $この積分項はベータ関数B(\cfrac{n-1}{2},\cfrac{1}{2})でガンマ関数を用いて$
$\quad B(\cfrac{n-1}{2},\cfrac{1}{2})=\cfrac{\Gamma(\dfrac{n-1}{2})\Gamma(\dfrac{1}{2})}{\Gamma(\dfrac{n-1}{2}+\dfrac{1}{2})}= \cfrac{\sqrt{\pi}\ \Gamma(\dfrac{n-1}{2})}{\Gamma(\dfrac{n}{2})}$
$よって$
\begin{eqnarray*} f_n(x) &=&C_1C_{n-1} \sqrt{\pi} \cfrac{\Gamma(\dfrac{n-1}{2})}{\Gamma(\dfrac{n}{2})} x^{\small{\dfrac{n-2}{2}}}e^{\small{-\dfrac{x}{2}}}\\ \\ &=&\cfrac{C_{n-1}}{\sqrt{2}}\cfrac{\Gamma(\dfrac{n-1}{2})}{\Gamma(\dfrac{n}{2})} x^{\small{\dfrac{n-2}{2}}}e^{\small{-\dfrac{x}{2}}}\\ \end{eqnarray*} $したがって \quad C_n=\cfrac{\Gamma(\dfrac{n-1}{2})}{\sqrt{2}\ \Gamma(\dfrac{n}{2})}C_{n-1} \ \ とおくと$
$\quad f_n(x)=C_n x^{\small{\dfrac{n-2}{2}}}e^{\small{-\dfrac{x}{2}}} \ \ となって、k=n のときも成りたつ。$
$次にこの漸化式を解きましょう。$
$C_n=\cfrac{\Gamma(\dfrac{n-1}{2})}{\sqrt{2}\ \Gamma(\dfrac{n}{2})}C_{n-1} \ \ より$
$\Gamma(\dfrac{n}{2})C_n=\cfrac{1}{\sqrt{2}}\Gamma(\dfrac{n-1}{2})C_{n-1}$
$p_n=\Gamma(\dfrac{n}{2})C_n \ \ とおくと$
$p_n=\cfrac{1}{\sqrt{2}}p_{n-1} \ \ となって p_1=\Gamma(\dfrac{1}{2})C_1=\sqrt{\pi} \times \cfrac{1}{\sqrt{2\pi}}=\cfrac{1}{\sqrt{2}}$
$\therefore p_n=\cfrac{1}{\sqrt{2}} \times \bigl(\cfrac{1}{\sqrt{2}}\bigr)^{n-1}=\bigl(\cfrac{1}{\sqrt{2}}\bigr)^n=\cfrac{1}{2^{\small \dfrac{n}{2}}}$
$よって \quad C_n=\cfrac{1}{2^{\small \dfrac{n}{2}}\Gamma(\dfrac{n}{2})}$
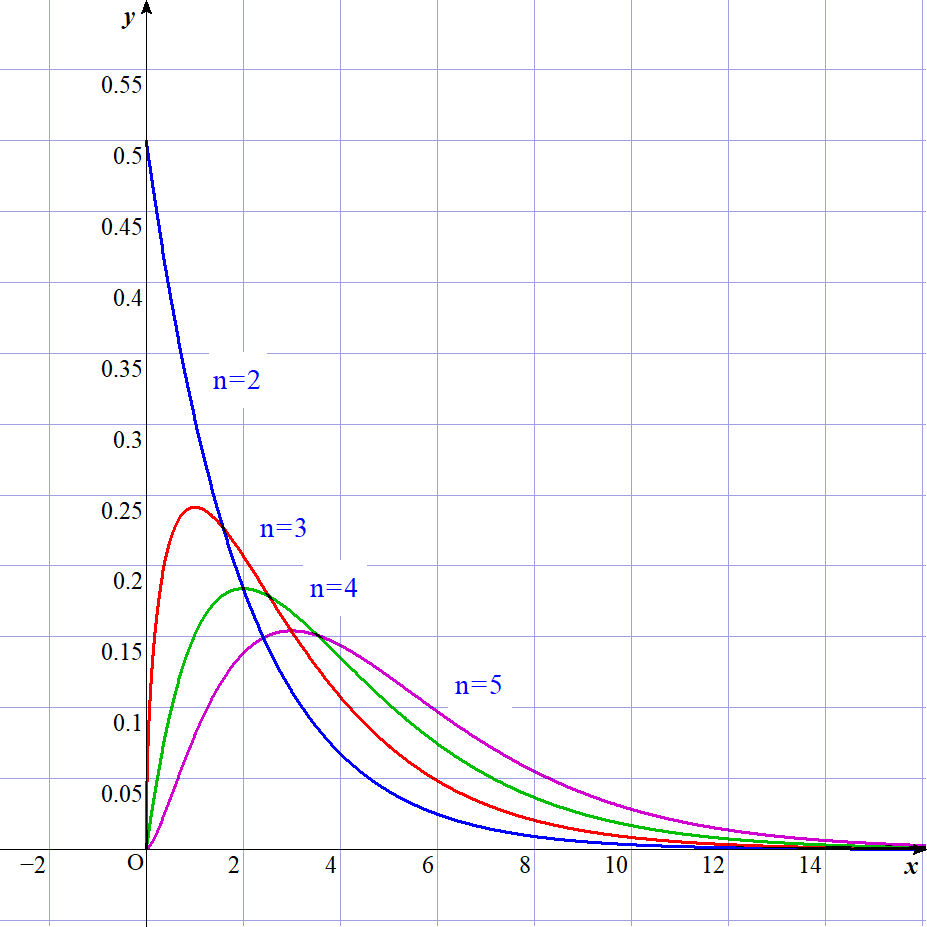
$したがって \quad f_n(x)=\cfrac{1}{2^{\small \dfrac{n}{2}}\Gamma(\dfrac{n}{2})} x^{\small{\dfrac{n-2}{2}}}e^{\small{-\dfrac{x}{2}}}$
$これを、自由度nの\chi ^2 分布といい、\chi _n ^2 \ \ とあらわします。$
χ(カイ)2乗分布メニュー に戻る