千葉大学(理系) 2024年 問題8
$半径 \ 1、中心 \ O\ の円 \ C\ がある。2\ つの円 \ C_1 と \ C_2 \ が次の \ 2\ つの条件を満たすとする。$
$\qquad ・C_1 \ と \ C_2\ はどちらも \ C\ に内接する。$
$\qquad ・C_1\ と \ C_2\ は互いに外接する。$
$円C_1 、C_2\ の中心をそれぞれ \ D,\ E\ とし、半径をそれぞれ \ p,\ q\ とする。 \theta=\angle DOE \ \ とおく。$
$以下の問いに答えよ。$
$(1)\ \ q\ を \ p\ と \ \theta \ を用いて表せ、$
$(2)\ \ p\ を固定する。\theta \ が \ 0\ に近づくとき、\dfrac{q}{\theta ^2} \ \ の極限値を求めよ。$
$さらに、円 \ C_3\ が次の \ 2\ つの条件を満たすとする。$
$\qquad ・C_3 \ と \ C_1\ は半径が等しい。$
$\qquad ・C_3 \ は \ C\ に内接し、C_1 \ と \ C_2\ のどちらとも外接する。$
$このとき以下の問いに答えよ。$
$(3)\ \ p=\sqrt{2}-1 \ \ のとき、q\ の値を求めよ。$
$(4)\ \ \theta が \ 0\ に近づくとき、\dfrac{q}{p}\ \ の極限値を求めよ。$
(1)
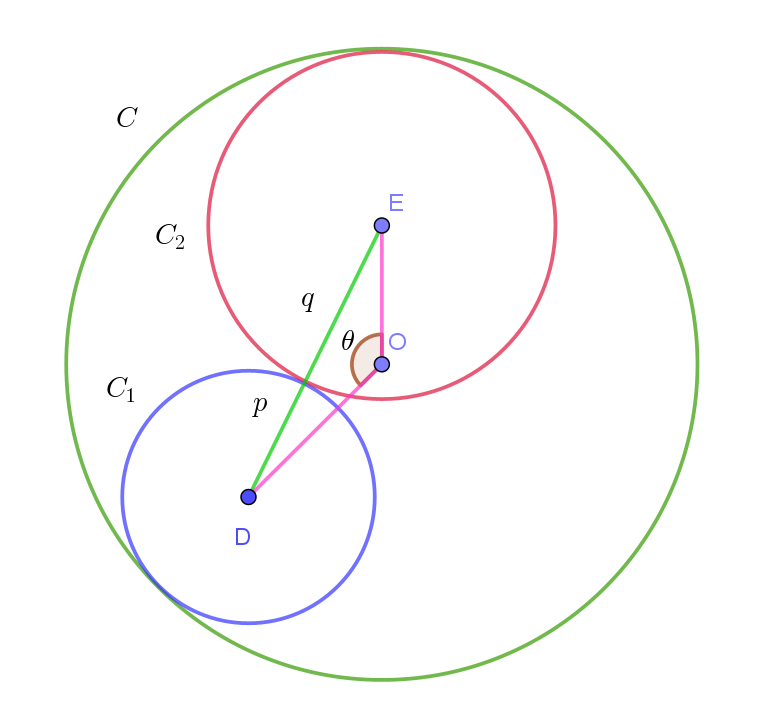
$DE^2=OD^2+OE^2-2OD \cdot OE \cos \theta$
$条件より\ \ DE=p+q ,\quad OD=1-p,\quad OE=1-q \quad だから$
$(p+q)^2=(1-p)^2+(1-q)^2-2(1-p)(1-q)\cos \theta$
$pq=1-p-q-(1-p)(1-q)\cos \theta$
$q\big(1+p-(1-p)\cos \theta \big)=(1-p)(1-\cos \theta)$
$ここで \ \ 0 < p <1 , \quad 0 < \theta < \pi \ \ だから \quad 1+p >1$
$0 < 1-p < 1 \quad \therefore \ \ -1 < (1-p)\cos \theta < 1$
$よって \quad 1+p-(1-p)\cos \theta > 0 \quad だから$
$q=\cfrac{(1-p)(1-\cos \theta)}{1+p-(1-p)\cos \theta}$
(2)
\begin{eqnarray*} q &=&\cfrac{(1-p)(1-\cos \theta)}{1+p-(1-p)\cos \theta}\\ \\ &=&\cfrac{(1-p)\big\{1-(1-2\sin ^2 \dfrac{\theta}{2}\big\}}{1+p-(1-p)\cos \theta}\\ \\ &=&\cfrac{2(1-p)\sin ^2 \dfrac{\theta}{2}}{1+p-(1-p)\cos \theta}\\ \end{eqnarray*}
$したがって$
\begin{eqnarray*} & &\lim _{\theta \longrightarrow 0 } \cfrac{q}{\theta ^2}\\ \\ &=&\lim _{\theta \longrightarrow 0 }\cfrac{2(1-p)}{1+p-(1-p)\cos \theta} \cdot \cfrac{\sin ^2 \dfrac{\theta}{2}}{\theta ^2}\\ \\ &=&\lim _{\theta \longrightarrow 0 }\cfrac{1-p}{2\big\{1+p-(1-p)\cos \theta \big\}} \cdot \Big(\cfrac{\sin \dfrac{\theta}{2}}{\dfrac{\theta }{2}}\Big)^2\\ \\ &=&\lim _{\theta \longrightarrow 0 } \cfrac{1-p}{2\big\{1+p-(1-p)\cos \theta \big\}} \cdot \Big(\cfrac{\sin \dfrac{\theta}{2}}{\dfrac{\theta }{2}}\Big)^2\\ \\ &=&\cfrac{1-p}{2\big\{1+p-(1-p) \big\}}\\ \\ &=&\cfrac{1-p}{4p}\\ \end{eqnarray*}
(3)
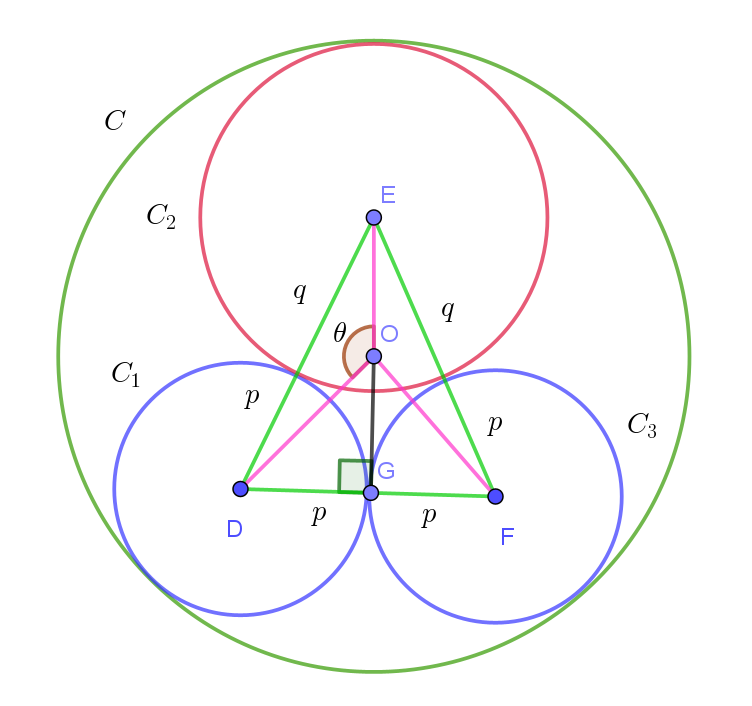
$G\ は \ DF\ の中点である。$
$\triangle EDF\ は \ ED=EF\ の二等辺三角形だから \ \ EG \perp DF$
$\triangle ODF\ は \ OD=OF\ の二等辺三角形だから \ \ OG \perp DF$
$したがって 3\ 点 \ E,\ O,\ G\ は一直線上にあるから \quad \angle DOG=\pi -\theta $
$直角三角形 \ ODG\ において$
$\sin \angle DOG=\cfrac{DG}{OD}$
$\sin (\pi-\theta)=\cfrac{p}{1-p}$
$\sin \theta=\cfrac{p}{1-p}$
$とくに \quad p=\sqrt{2}-1 \quad のとき$
$\sin \theta=\cfrac{\sqrt{2}-1}{1-(\sqrt{2}-1)}=\cfrac{\sqrt{2}-1}{2-\sqrt{2}}=\cfrac{1}{\sqrt{2}}$
$したがって \quad \theta=\cfrac{\pi}{4},\quad \cfrac{3}{4}\pi$
$(1)より \quad q=\cfrac{(1-p)(1-\cos \theta)}{1+p-(1-p)\cos \theta} \quad だから$
$\theta=\cfrac{\pi}{4} \quad のとき \quad q=\cfrac{(2-\sqrt{2})(1-\dfrac{1}{\sqrt{2}})}{\sqrt{2}-(2-\sqrt{2}) \times \dfrac{1}{\sqrt{2}}}=3-2\sqrt{2}$
$\theta=\cfrac{3}{4}\pi \quad のとき \quad q=\cfrac{(2-\sqrt{2})(1+\dfrac{1}{\sqrt{2}})}{\sqrt{2}-(2-\sqrt{2}) \times \big(-\dfrac{1}{\sqrt{2}}\big)}=\cfrac{2\sqrt{2}+1}{7}$
$(別解)$
$条件より \quad DF=2p $
$\triangle ODE\ と \ \triangle OFE \ \ において、3\ 辺が等しいから \quad \triangle ODE \equiv \triangle OFE$
$したがって \quad \angle DOE=\angle FOE=\theta$
$\therefore \angle DOF=2\pi -2\theta$
$\triangle ODF \ \ に余弦定理をもちいて$
$DF^2=OD^2+OF^2-2OD \cdot OF \cos \angle DOF$
$4p^2=(1-p)^2+(1-p)^2-2(1-p)^2\cos (2\pi-2\theta)$
$4p^2=2(1-p)^2-2(1-p)^2\cos 2\theta$
$2p^2=(1-p)^2-(1-p)^2\cos 2\theta$
$\cos 2\theta=\cfrac{(1-p)^2-2p^2}{(1-p)^2}$
$とくに \quad p=\sqrt{2}-1 \quad のとき$
$\cos 2\theta=\cfrac{(2-\sqrt{2})^2-2(\sqrt{2}-1)^2}{(2-\sqrt{2})^2}=0$
$0 < \theta < \pi \quad だから \quad 2\theta=\cfrac{\pi}{2},\quad \cfrac{3}{2}\pi \qquad \therefore \ \theta=\cfrac{\pi}{4},\quad \cfrac{3}{4}\pi$
(4)
$(3)より \sin \theta=\cfrac{p}{1-p} だから$
$(1-p)\sin \theta=p \qquad (1+\sin \theta)p=\sin \theta \qquad 1+\sin \theta \ne 0 \quad だから$
$p=\cfrac{\sin \theta}{1+\sin \theta}$
$(1) より$
\begin{eqnarray*} q &=&\cfrac{(1-p)(1-\cos \theta)}{1+p-(1-p)\cos \theta}\\ \\ &=&\cfrac{(1-\cfrac{\sin \theta}{1+\sin \theta})(1-\cos \theta)}{1+\cfrac{\sin \theta}{1+\sin \theta}-(1-\cfrac{\sin \theta}{1+\sin \theta})\cos \theta}\\ \\ &=&\cfrac{1-\cos \theta}{(1+\sin \theta)+\sin \theta - \cos \theta }\\ \\ &=&\cfrac{1-\cos \theta}{1+2\sin \theta - \cos \theta }\\ \end{eqnarray*}
$したがって$
\begin{eqnarray*} \cfrac{q}{p} &=&\cfrac{\cfrac{1-\cos \theta}{1+2\sin \theta - \cos \theta }}{\cfrac{\sin \theta}{1+\sin \theta}}\\ \\ &=&\cfrac{(1+\sin \theta )(1-\cos \theta)}{\sin \theta (1+2\sin \theta -\cos \theta)}\\ \\ &=&\cfrac{(1+\sin \theta )(2\sin ^2 \dfrac{\theta}{2})}{\sin \theta (4\sin \dfrac{\theta}{2} \cos \dfrac{\theta}{2} + 2\sin ^2 \dfrac{\theta}{2})}\\ \\ &=&\cfrac{(1+\sin \theta )\sin \dfrac{\theta}{2}}{\sin \theta (2\cos \dfrac{\theta}{2} + \sin \dfrac{\theta}{2})}\\ \\ &=&\cfrac{(1+\sin \theta )\sin \dfrac{\theta}{2}}{2\sin \dfrac{\theta}{2}\cos \dfrac{\theta}{2} (2\cos \dfrac{\theta}{2} + \sin \dfrac{\theta}{2})}\\ \\ &=&\cfrac{1+2\sin \dfrac{\theta}{2}\cos \dfrac{\theta}{2}}{2\cos \dfrac{\theta}{2} (2\cos \dfrac{\theta}{2} + \sin \dfrac{\theta}{2})}\\ \\ &=&\cfrac{(\sin \dfrac{\theta}{2} + \cos \dfrac{\theta}{2})^2}{2\cos \dfrac{\theta}{2} (2\cos \dfrac{\theta}{2} + \sin \dfrac{\theta}{2})}\\ \end{eqnarray*}
\[ゆえに \quad \lim_{\theta \rightarrow 0}\cfrac{q}{p}=\cfrac{1}{4}\]
メインメニュー に戻る