千葉大学(理系) 2024年 問題7
$n\ を正の整数とする。x\ の関数 \ f(x)=x^3-2nx^2+(2n-3)x+1 \ \ について以下の問いに答えよ。$
$(1)\ \ \alpha \ を \ f(x)=0 \ の \ 1\ つの解とする。f(\dfrac{1}{1-\alpha})\ \ の値を求めよ。$
$(2)\ \ 方程式 \ f(x)=0 \ \ は異なる \ 3\ つの実数解をもつことを示せ。$
\[(3)\ \ 方程式 \ f(x)=0\ \ の解で \ 2\ 番目に大きいものを \ \beta_n \ とする。極限値 \ \ \lim_{n \rightarrow \infty} \beta_n \ \ を求めよ。\]
(1)
$f(1)=1-2n+(2n-3)+1=-1 \quad だから \quad f(1) \ne 0 $
$\alpha \ は \ f(x)=0 \ の \ 1\ つの解だから \quad f(\alpha)=0 \quad ただし \quad \alpha \ne 1$
$このとき$
\begin{eqnarray*} f(\dfrac{1}{1-\alpha}) &=&\cfrac{1}{(1-\alpha)^3}-\cfrac{2n}{(1-\alpha)^2}+\cfrac{2n-3}{1-\alpha}+1\\ \\ &=&\cfrac{1-2n(1-\alpha) + (2n-3)(1-\alpha)^2+(1-\alpha)^3}{(1-\alpha)^3}\\ \\ &=&\cfrac{-1+(-2n-3)\alpha +2n\alpha ^2 - \alpha ^3}{(1-\alpha)^3}\\ \\ &=&-\cfrac{f(\alpha)}{(1-\alpha)^3}\\ \\ &=&0 \end{eqnarray*}
(2)
$代数的な解法$
$\beta =\cfrac{1}{1-\alpha } \quad とおくと$
$(1)より \ \ f(\beta)=0 \ \ だから \ \ \beta \ は \ f(x)=0 \ の解である。$
$すると (1)より\quad \gamma=\cfrac{1}{1-\beta} \quad も解であるから$
$\gamma =\cfrac{1}{1-\beta} =\cfrac{1}{1-\cfrac{1}{1-\alpha}}=\cfrac{1-\alpha }{(1-\alpha)- 1 }=-\cfrac{1-\alpha }{\alpha }$
$\delta =\cfrac{1}{1-\gamma} \quad も解であるから$
$\delta =\cfrac{1}{1-\gamma} =\cfrac{1}{1+\cfrac{1-\alpha}{\alpha}}=\alpha $
$これ以上新しい解を作れないから、f(x)=0 \ の解は \ \ \alpha ,\ \ \cfrac{1}{1-\alpha},\ \ \cfrac{\alpha -1}{\alpha}\ \ の \ 3\ つである。$
$一般に、3次方程式 \ f(x)=0\ は高々 \ 3\ 個の解をもつが \ \ (代数学の基本定理)$
(i)$\ \ 3\ つの実数解(重解も含めて)$
(ii)$\ \ 1\ つの実数解と \ 2\ つの共役な複素数解$
(i),(ii)$\ \ のうちどちらか一方だけが成りたつ。$
$\alpha \ が虚数解ならば、この共役複素数 \ \overline{\alpha}\ も解であるから$
$\quad \overline{\alpha}=\cfrac{1}{1-\alpha} \quad とすると$
$\quad \overline{\alpha}(1-\alpha )=1$
$\quad \overline{\alpha} =1+ |\alpha|^2 $
$\quad 左辺は虚数、右辺は実数だからこれは不合理$
$\quad \overline{\alpha}=\cfrac{\alpha -1}{\alpha} \quad とすると$
$\quad |\alpha |^2=\alpha -1$
$\quad \alpha =1+ |\alpha|^2 $
$\quad 左辺は虚数、右辺は実数だからこれは不合理$
$したがって \ \ \alpha \ は実数である。$
$実数は四則演算について閉じているので、\cfrac{1}{1-\alpha},\ \ \cfrac{\alpha -1}{\alpha}\ \ も実数である。$
$次に、\alpha 、\ \ \cfrac{1}{1-\alpha}, \ \ \cfrac{\alpha -1}{\alpha}\ \ がすべて異なることの証明。$
$\alpha=\cfrac{1}{1-\alpha} \quad とすると$
$\alpha (1-\alpha)=1 \qquad \alpha ^2-\alpha +1=0 \qquad \alpha \ は虚数$
$\alpha=\cfrac{\alpha -1}{\alpha} \quad とすると$
$\alpha \alpha ^2=\alpha -1 \qquad \alpha ^2-\alpha +1=0 \qquad \alpha \ は虚数$
$\cfrac{1}{1-\alpha}=\cfrac{\alpha -1}{\alpha} \quad とすると$
$\alpha =-(\alpha -1)^2 \qquad \alpha ^2-\alpha +1=0 \qquad \alpha \ は虚数$
$\alpha \ は実数だからすべて不合理$
$よって \quad \alpha 、\ \ \cfrac{1}{1-\alpha},\ \ \cfrac{\alpha -1}{\alpha}\ \ はすべて異なる。$
$以上で、方程式 \ f(x)=0 \ \ は異なる \ 3\ つの実数解をもつ。$
$解析的な解法$
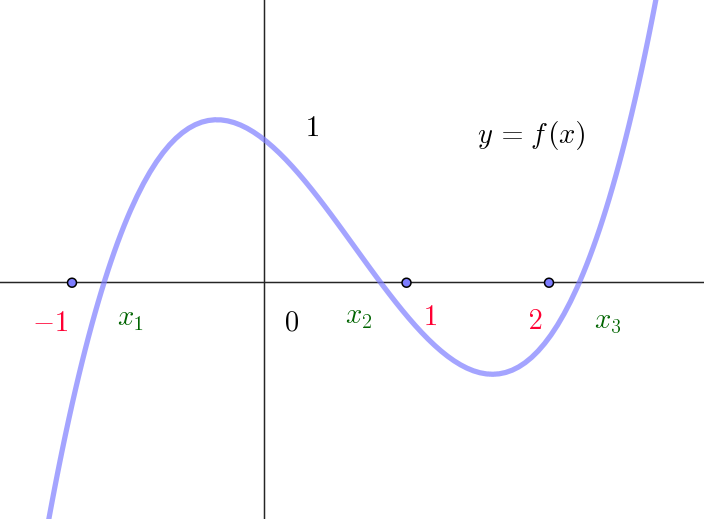
$3\ 次関数である。$
$f(-1)=-1-2n-2n+3+1=-4n+3<0$
$f(0)=1>0$
$f(1)=1-2n+2n-3+1=-1<0$
$f(2)=8-8n+4n-6+1=-4n+3<0$
$十分大きな \ x > 2\ の \ x\ に対して、f(x) > 0$
$中間値の定理より$
$区間 \ (-1,\ 0)\ に実数解 \ x_1\ が存在する。$
$区間 \ (0.\ 1)\ に実数解 \ x_2\ が存在する。$
$区間 \ x > 2 \ に実数解 \ x_3\ が存在する。$
(3)
$\beta_n=x_2 \ \ だから \quad 0 < \beta_n <1$
\begin{eqnarray*} f\big(1-\cfrac{1}{n}\big) &=&\big(1-\cfrac{1}{n}\big)^3-2n\big(1-\cfrac{1}{n}\big)^2+(2n-3)\big(1-\cfrac{1}{n}\big)+1\\ \\ &=&\big(1-\cfrac{3}{n}+ \cfrac{3}{n^2} -\cfrac{1}{n^3}\big)-2n\big(1-\cfrac{2}{n}+\cfrac{1}{n^2}\big)^2+(2n-3)\big(1-\cfrac{1}{n}\big)+1\\ \\ &=&1-\cfrac{2}{n}+ \cfrac{3}{n^2} -\cfrac{1}{n^3} \\ \\ &>&1-\cfrac{2}{n} -\cfrac{1}{n^3} \\ \\ &>&1-\cfrac{2}{n} -\cfrac{1}{n} \\ \\ &=&1-\cfrac{3}{n}\\ \\ &=&\cfrac{n-3}{n} \end{eqnarray*}
$ここで \quad n > 3 \quad のとき $
$f\big(1-\cfrac{1}{n}\big) > 0 \ \ だから中間値の定理より \quad 1-\cfrac{1}{n} < \beta_n <1$
$n \longrightarrow \infty \ \ のとき \quad 1-\cfrac{1}{n} \longrightarrow 1 \quad だからはさみうちの原理により$
\[\lim_{n \rightarrow \infty} \beta_n =1\]
$f\big(1-\cfrac{1}{n}\big) > 0 \quad の別証$
$f\big(1-\cfrac{1}{n}\big)=1-\cfrac{2}{n}+ \cfrac{3}{n^2} -\cfrac{1}{n^3}=\cfrac{n^3-2n^2+3n-1}{n^3}\quad より$
$g(x)=x^3-2x^2+3x-1 \ \ (x \ は \ \ x \geqq 1 \ \ の実数 )\ \ とおくと$
$g'(x)=3x^2-4x+3=3\big(x-\dfrac{2}{3}\big)^2+\dfrac{5}{3} > 0$
$g(x)\ は単調増加だから \quad g(x)> g(1)=1 > 0 $
$よって、すべての自然数 \ n\ について \quad \cfrac{n^3-2n^2+3n-1}{n^3} > 0 $
$したがって \quad f\big(1-\cfrac{1}{n}\big)>0 $
メインメニュー に戻る