千葉大学(理系) 2024年 問題6
$関数 \ f(x)=e^x+e^{-2x} \ \ について以下の問いに答えよ。$
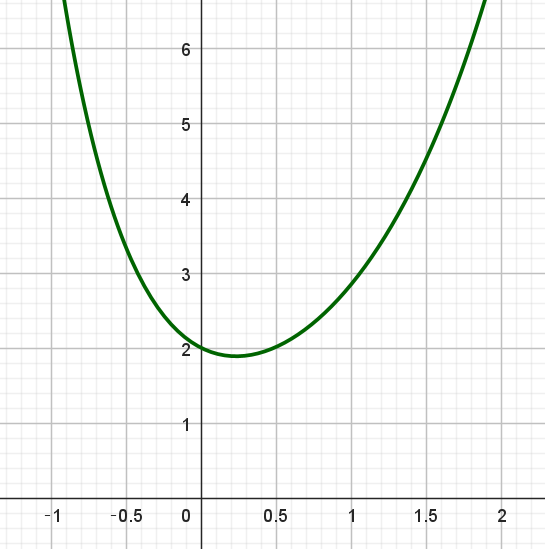
$(1)\ \ 関数 \ f(x)\ の最小値を求めよ。$
$(2)\ \ f(x)=2 \ \ となる \ x\ の値をすべて求めよ。$
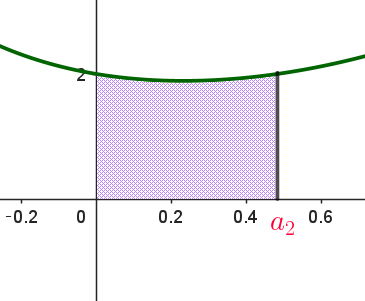
$(3)\ \ (2)で求めた \ x\ の値のうち最小のものを \ a_1、最大のものを \ a_2\ とする。y=f(x)\ \ のグラフ、x\ 軸、$
$\quad 直線 \ x=a_1,\ 直線 \ x=a_2 \ \ で囲まれる図形を \ x\ 軸の周りに \ 1\ 回転してできる立体の体積を求めよ。$
(1)
$f'(x)=e^x-2e^{-2x}=e^x-\dfrac{2}{e^{2x}}=\dfrac{e^{3x}-2}{e^{2x}}$
$f'(x)=0\ \ より \ \ e^{3x}=2 \quad 3x=\log 2 \quad x=\dfrac{1}{3}\log 2$
$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& \cdots & \dfrac{1}{3}\log 2 & \cdots \\ \hline f'(x)& - & 0 & + \\ \hline f(x)& \searrow & 極小 & \nearrow \\ \end{array} \]
$x=\cfrac{1}{3}\log 2 \ で\ f(x)\ は極小かつ最小となり、最小値は$
$e^x=\sqrt[3]{2} \ \ より \ \ e^{2x}=\sqrt[3]{4}$
$\quad f(\dfrac{1}{3}\log 2)=\sqrt[3]{2}+ \cfrac{1}{\sqrt[3]{4}}=\sqrt[3]{2}+ \cfrac{\sqrt[3]{2}}{2}=\cfrac{3}{2}\sqrt[3]{2}$
(2)
$f(x)=e^x+e^{-2x}=2 \ \ の両辺に \ \ e^{2x}\ \ をかけて$
$e^{3x}+1=2e^{2x}$
$e^{3x}-2e^{2x}+1=0$
$e^x=t \ \ とおくと \ \ t > 0$
$t^3-2t^2+1=0$
$(t-1)(t^2-t-1)=0$
$t >\ 0\ \ だから \ \ t=1,\ \ \cfrac{1+\sqrt{5}}{2}$
$e^x=1 \ \ より \ \ x=0$
$e^x=\cfrac{1+\sqrt{5}}{2} \ \ より \ \ x=\log \cfrac{1+\sqrt{5}}{2}$
(3)
$(2)より \ \ a_1=0,\quad a_2=\log \cfrac{1+\sqrt{5}}{2}$
$e^{2a_2}=\big(\cfrac{1+\sqrt{5}}{2}\big)^2=\cfrac{3+\sqrt{5}}{2}$
$e^{-a_2}=\cfrac{2}{1+\sqrt{5}}=-\cfrac{1-\sqrt{5}}{2}$
$e^{-2a_2}=\big(-\cfrac{1-\sqrt{5}}{2}\big)^2=\cfrac{3-\sqrt{5}}{2}$
$e^{-4a_2}=\big(\cfrac{3-\sqrt{5}}{2}\big)^2=\cfrac{7-3\sqrt{5}}{2}$
\begin{eqnarray*} V &=&\pi \int_0^{a_2} y^2dx\\ \\ &=&\pi \int_0^{a_2} \big(e^x+e^{-2x}\big)^2dx\\ \\ &=&\pi \int_0^{a_2} \big(e^{2x}+2e^{-x}+e^{-4x}\big)dx\\ \\ &=&\pi \big[\dfrac{1}{2}e^{2x}-2e^{-x}-\dfrac{1}{4}e^{-4x}\big]_0^{a_2}\\ \\ &=&\pi \big\{\dfrac{1}{2}e^{2a_2}-2e^{-a_2}-\dfrac{1}{4}e^{-4a_2}-\big(\dfrac{1}{2}-2-\dfrac{1}{4}\big) \big\} \\ \\ &=&\pi \big\{\dfrac{1}{2} \times \cfrac{3+\sqrt{5}}{2} -2 \times \big( -\cfrac{1-\sqrt{5}}{2} \big) -\dfrac{1}{4} \times \cfrac{7-3\sqrt{5}}{2} +\dfrac{7}{4}\big\} \\ \\ &=&\cfrac{21-3\sqrt{5}}{8}\pi\\ \end{eqnarray*}
メインメニュー に戻る