千葉大学(理系) 2024年 問題5
$n \ を \ 3\ 以上の整数とする。座標平面上の \ 2n\ 個の点からなる集合 \ \{(x,\ y)|x=1,\ 2,\ 3,\ \cdots ,\ n,\ y=1,\ 2\}\ \ を$
$考える。この集合から異なる \ 3\ 点を無作為に選び、その \ 3\ 点を線分で結んで得られる図形の面積を \ X\ と$
$する。ただし、3\ 点が同一直線上にあるときは \ X=0\ とする。$
$(1)\ \ k\ が \ 0\ 以上の整数のとき、X\ が \ \dfrac{k}{2}\ となる確率 \ p_k \ を \ n\ と \ k\ の式で表せ。$
\[(2)\ \ X\ が \ \dfrac{n}{4}\ 以下となる確率を \ q_k \ とおく。\lim_{n \rightarrow \infty} q_n \ \ を求めよ。\]
(1)
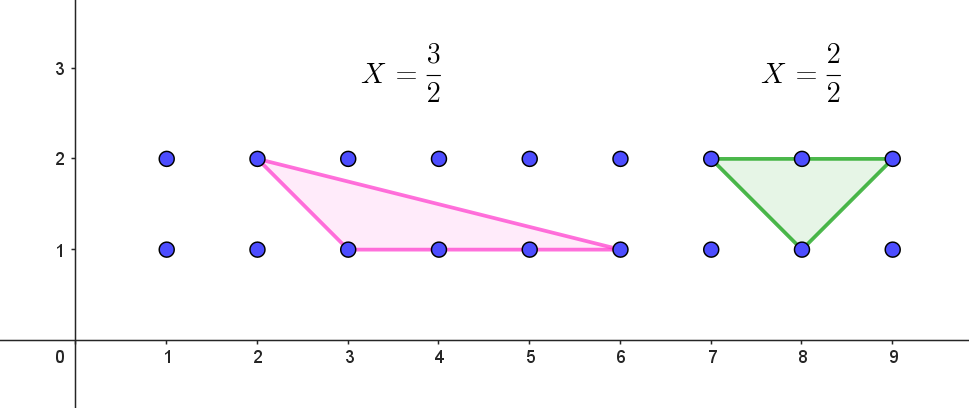
$\{(x,\ y)|x=1,\ 2,\ 3,\ \cdots ,\ n,\ y=1,\ 2\}$
$から異なる \ 3\ 点を無作為に選ぶ選び方は$
$N={}_{2n}C_3=\cfrac{2n(2n-1)(2n-2)}{6}=\cfrac{2n(2n-1)(n-1)}{3} \ \ 通り$
(i)$\ \ k=0 \ \ のとき \ \ X=0\ \ だから$
$\quad \{(x,\ 1)|x=1,\ 2,\ 3,\ \cdots , \ n\} から \ 3\ 点を選ぶ場合と、\{(x,\ 2)|x=1,\ 2,\ 3,\ \cdots , \ n\} から \ 3\ 点を選ぶ場合がある。$
$\quad 選び方の総数は \ \ n(X=0)={}_nC_3 \times 2=\cfrac{n(n-1)(n-2)}{6} \times 2=\cfrac{n(n-1)(n-2)}{3}$
$\quad よって \quad p_0=\cfrac{n(X=0)}{N}=\cfrac{\dfrac{n(n-1)(n-2)}{3}}{\dfrac{2n(2n-1)(n-1)}{3}}=\cfrac{n-2}{2(2n-1)}$
(ii)$\ \ 1 \leqq k \leqq n-1 \ \ のとき \ \ X=\cfrac{k}{2} \ \ となるのは$
$(ア)\ \ 底辺を \ (x,\ 1)\ でとる場合$
$\quad 底辺は、(1,1)\ と (k+1,1),\ \ (2,1)\ と \ (k+2,1),\ \ \cdots ,(n-k,1)\ と \ (n,1)\ \ を結ぶ \ \ (n-k)\ 通り$
$\quad 高さは、(1,2),\ \ (2,2),\ \ \cdots , (n,2) \ \ の \ n\ 通り$
$(イ)\ \ 底辺を \ (x,\ 2)\ でとる場合$
$\quad 底辺は、(1,2)\ と \ (k+1,2),\ \ (2,2)\ と \ (k+2,2),\ \ \cdots ,(n-k,2)\ と \ (n,2)\ \ を結ぶ \ \ (n-k)\ \ 通り$
$\quad 高さは、(1,1),\ \ (2,1),\ \ \cdots , (n,1)\ の \ n\ 通り$
$(ア)と(イ)は互いに排反だから、選び方の総数は$
$\quad n(X=\cfrac{k}{2})=(n-k) \times n \times 2=2n(n-k) \ \ 通り$
$\quad p_k=\cfrac{n(X=\cfrac{k}{2})}{N}=\cfrac{2n(n-k)}{\dfrac{2n(2n-1)(n-1)}{3}}=\cfrac{3(n-k)}{(2n-1)(n-1)}$
(iii)$\ \ k \geqq n \ \ のとき $
$\quad \{(x,\ y)|x=1,\ 2,\ 3,\ \cdots ,\ n,\ y=1,\ 2\}\ \ から 底辺が \ k\ となる \ 2\ 点を選ぶことができないから \ \ p_k=0$
(i),(ii),(iii)$\ \ より$
\[ \hspace{1em} p_k= \left\{ \begin{array}{l} \dfrac{n-2}{2(2n-1)} \hspace{6em}(\ k=0\ )\\ \\ \dfrac{3(n-k)}{(2n-1)(n-1)} \hspace{3em}(\ 1 \leqq k \leqq n-1\ )\\ \\ 0 \hspace{10em}(\ k \geqq n \ )\\ \end{array} \right. \]
(2)
$X\ が正で、\dfrac{n}{4}\ 以下であるということは、三角形の高さは \ 1\ だから、底辺が \ \dfrac{n}{2}\ 以下ということである。$
$k\ が \ \ 1 \leqq k \leqq \big[\dfrac{n}{2}\big] \ \ の整数のとき \ \ (\big[\dfrac{n}{2}\big]\ は \ \dfrac{n}{2}\ を超えない最大の整数を表し、ガウス記号という) $
$\cfrac{n}{2} < n-1 \ \ であるから(1)より$
\begin{eqnarray*} q_n &=&p_0+\sum_{k=1}^{[\dfrac{n}{2}]}p_k\\ \\ &=&p_0 +\sum_{k=1}^{[\dfrac{n}{2}]} \dfrac{3(n-k)}{(2n-1)(n-1)}\\ \\ &=&p_0 +\cfrac{3}{(2n-1)(n-1)}\sum_{k=1}^{[\dfrac{n}{2}]} (n-k)\\ \end{eqnarray*}
(i)$\ \ n\ が奇数のとき \quad [\cfrac{n}{2}]=\cfrac{n-1}{2}=m \quad とおくと$
\begin{eqnarray*} \quad q_n &=&p_0 +\cfrac{3}{(2n-1)(n-1)}\sum_{k=1}^m (n-k)\\ \\ &=&p_0 +\cfrac{3}{(2n-1)(n-1)} \big\{mn - \cfrac{m}{2}(m+1) \big\}\\ \\ &=&p_0 +\cfrac{3m}{(2n-1)(n-1)} \big(n - \cfrac{m+1}{2}\big)\\ \\ &=&p_0 +\cfrac{3(n-1)}{2(2n-1)(n-1)} \big(n - \cfrac{n+1}{4}\big)\\ \\ &=&\cfrac{n-2}{2(2n-1)} + \cfrac{3(n-1)(3n-1)}{8(2n-1)(n-1)}\\ \\ &=&\dfrac{13n^2-24n+11}{8(2n-1)(n-1)}\\ \end{eqnarray*}
$\quad n \longrightarrow \infty \quad のとき \quad q_n \longrightarrow \cfrac{13}{16}$
(ii)$\ \ n が偶数のとき \quad [\cfrac{n}{2}]=\cfrac{n}{2}=m \quad とおくと$
\begin{eqnarray*} \quad q_n &=&p_0 +\cfrac{3}{(2n-1)(n-1)}\sum_{k=1}^m (n-k)\\ \\ &=&p_0 +\cfrac{3}{(2n-1)(n-1)} \big\{mn - \cfrac{m}{2}(m+1) \big\}\\ \\ &=&p_0 +\cfrac{3m}{(2n-1)(n-1)} \big(n - \cfrac{m+1}{2}\big)\\ \\ &=&p_0 +\cfrac{3n}{2(2n-1)(n-1)} \big(n - \cfrac{n+2}{4}\big)\\ \\ &=&\cfrac{n-2}{2(2n-1)} + \cfrac{3n(3n-2)}{8(2n-1)(n-1)}\\ \\ &=&\dfrac{13n^2-18n+8}{8(2n-1)(n-1)}\\ \end{eqnarray*}
$\quad n \longrightarrow \infty \quad のとき \quad q_n \longrightarrow \cfrac{13}{16}$
$したがって、n\ が奇数、偶数によらず$
\[\lim_{n \rightarrow \infty} q_n =\cfrac{13}{16}\]
メインメニュー に戻る