MY MATH NOTE

千葉大学(理系) 2018年　問題3

$正方形 \ ABCD\ の辺を除く内部に、PA \perp PB\ を満たす点 \ P\ がある。ベクトル \ \ \vec{PC}\ を \ \ x\vec{PA}+y\vec{PB}\ \ と$
$表すとき、以下の問いに答えよ。$
$(1)\ \ \alpha =\cfrac{|\vec{PB}|}{|\vec{PA}|}\ \ とするとき、x,\ y\ を \ \alpha \ を用いて表せ。$
$(2)\ \ 点 \ P\ が題意の条件を満たしながら動くとき、(1)で求めた \ x,\ y\ の和 \ x+y \ の最大値を求め、$
$\quad そのときの \ P\ がどのような点かを答えよ。$

(1)

　
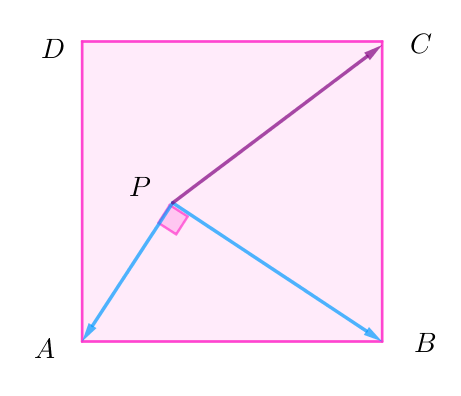
$PA \perp PB \quad より　\quad \vec{PA}\cdot \vec{PB}=0$

$\vec{PC}=x\vec{PA}+y\vec{PB}\quad より$

$\quad \vec{PA} \cdot \vec{PC}=x\vec{PA}\cdot \vec{PA}+y\vec{PA}\cdot \vec{PB}=x|\vec{PA}|^2$

$\quad \vec{PB} \cdot \vec{PC}=x\vec{PA}\cdot \vec{PB}+y\vec{PB}\cdot \vec{PB}=y|\vec{PB}|^2$

$\quad |\vec{PC}|^2=|x\vec{PA}+y\vec{PB}|^2=x^2|\vec{PA}|^2+2xy\vec{PA}\cdot \vec{PB}+y^2|\vec{PB}|^2=x^2|\vec{PA}|^2+y^2|\vec{PB}|^2$

$\alpha =\cfrac{|\vec{PB}|}{|\vec{PA}|}$

$四角形 \ ABCD\ は正方形であることを、これらを用いて表すと$

(i)$\ \ \angle ABC=90°\ \ だから \quad \vec{BA}\cdot \vec{BC}=0 \quad より$

$\quad (\vec{PA}-\vec{PB})\cdot (\vec{PC}-\vec{PB})=0$

$\quad \vec{PA} \cdot \vec{PC}-\vec{PA} \cdot \vec{PB}-\vec{PB} \cdot \vec{PC}+\vec{PB} \cdot \vec{PB}=0$

$\quad x|\vec{PA}|^2 -y|\vec{PB}|^2 +|\vec{PB}|^2=0$

$\quad x|\vec{PA}|^2 =(y-1)|\vec{PB}|^2 $

$\quad x=(y-1)\Big(\cfrac {|\vec{PB}|}{|\vec{PA}|}\Big)^2 $

$\quad x=\alpha ^2 (y-1) \hspace{10em}①$


(ii)$\ \ BA=BC \quad だから \quad |\vec{BA}|=|\vec{BC}| \quad より$

$\quad |\vec{PA}-\vec{PB}|^2=|\vec{PC}-\vec{PB}|^2$

$\quad |\vec{PA}|^2 -2\vec{PA}\cdot \vec{PB}+|\vec{PB}|^2=|\vec{PC}|^2-2\vec{PB} \cdot \vec{PC}+|\vec{PB}|^2$

$\quad |\vec{PA}|^2 =|\vec{PC}|^2-2\vec{PB} \cdot \vec{PC}$

$\quad |\vec{PA}|^2 =(x^2|\vec{PA}|^2+y^2|\vec{PB}|^2)-2y|\vec{PB}|^2$

$\quad (1-x^2)|\vec{PA}|^2 =(y^2 -2y)|\vec{PB}|^2 $

$\quad 1-x^2 =(y^2 -2y) \Big(\cfrac {|\vec{PB}|}{|\vec{PA}|}\Big)^2 $

$\quad 1-x^2 =\alpha ^2 (y^2 -2y) \hspace{10em}② $

$①を②に代入して$
$\quad 1-\alpha ^4(y-1)^2=\alpha ^2(y^2 -2y)$
$\quad (\alpha ^4+\alpha ^2)y^2 -2(\alpha ^4+\alpha ^2)y+\alpha ^4-1=0$
$\quad \alpha ^2(\alpha ^2+1)y^2 -2\alpha ^2(\alpha ^2+1)y+(\alpha ^2+1)(\alpha ^2-1)=0$
$\quad \alpha ^2 y^2 -2\alpha ^2 y+ \alpha ^2-1=0$
$\quad (\alpha y -(\alpha -1))(\alpha y -( \alpha +1))=0$

$\qquad \therefore \ \ y=\cfrac{\alpha -1}{\alpha},\quad \cfrac{\alpha +1}{\alpha}$

$①に代入して$

$\qquad y=\cfrac{\alpha -1}{\alpha} \quad のとき \quad x=\alpha ^2 \big(\cfrac{\alpha -1}{\alpha}-1\big)=\alpha ^2 \times (-\cfrac{1}{\alpha})=-\alpha $

$\qquad y=\cfrac{\alpha +1}{\alpha} \quad のとき \quad x=\alpha ^2 \big(\cfrac{\alpha +1}{\alpha}-1\big)=\alpha ^2 \times \cfrac{1}{\alpha} =\alpha $

　
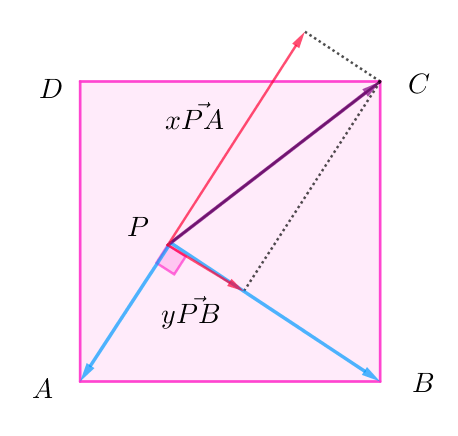
$\vec{PC}\ の \ \vec{PA}\ 方向の成分は、明らかに \ \vec{PA}\ と逆向きであるから \ \ x < 0$

$したがって \qquad x=-\alpha ,\quad y=\cfrac{\alpha -1}{\alpha}$

(2)

　
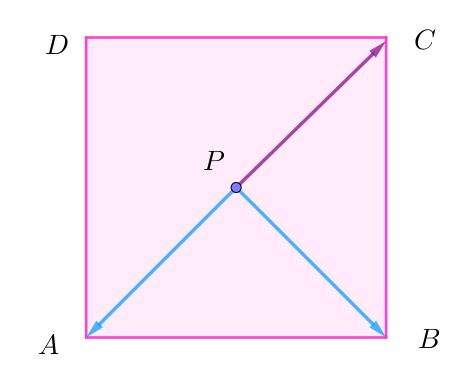
$\quad x+y \leqq 1-2=-1 \quad よって \quad x+y \ \ の最大値は \ \ -1$

$\qquad ただし \ \ 等号は \quad \alpha =\cfrac{1}{\alpha} \quad のときで、\alpha ^2=1 \quad より \quad 　\alpha =1 $

$このとき \quad x=-1,\quad y=0 \quad だから \quad \vec{PC}=-\vec{PA} \quad となり点 \ P\ は$
$AC\ の中点である。$



$(1)の別解$

$三角比を用いた図形的な解答を考えます。$

$\angle APB=90°であるから円周角の逆定理より　点 \ P\ は線分 \ AB\ を直径とする円周上にある。$
$点 \ A\ を原点とし、AB\ 方向を \ x軸、AD\ 方向を \ y\ 軸とした座標軸を考える。$

　
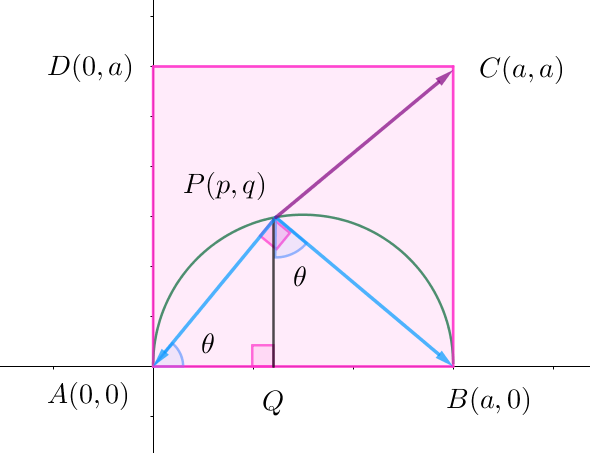
$A(0,\ 0),\ B(a,\ 0),\ C(a,\ a),\ D(0,\ a),\ P(p,\ q)\ \ とし、$
$\angle BAP=\theta \quad とする。$

$点 \ P\ から \ x\ 軸に下ろした垂線の足を \ Q\ とすると、$
$\angle BPQ=\theta \quad でもある。$

$AP=AB\cos \theta=a\cos \theta$
$p=AP\cos \theta=a\cos ^2\theta ,\quad q=AP\sin \theta=a\cos \theta \sin \theta$

$\alpha=\cfrac{PB}{PA}=\tan \theta$

$これらの準備のもとで \quad \vec{PC}=x\vec{PA}+y\vec{PB}\ \ を成分表示すると$

$\qquad \vec{AC}-\vec{AP}=x(-\vec{AP})+y(\vec{AB}-\vec{AP})$

$\qquad (a,a)-(p,q)=-x(p,q)+y\{(a,0)-(p,q)\}$
\[ \hspace{1em} \left\{ \begin{array}{l} a-p=-px+(a-p)y \ \hspace{5em}(1)\\ a-q=-qx-qy \hspace{8em}(2)\\ \end{array} \right. \]
$(1)\times q+(2) \times (a-p) \quad より$
$\quad a(a-p)=-aqx$

$\quad x=-\cfrac{a-p}{q}=-\cfrac{BH}{PH}=-\tan \theta=-\alpha$

$(1)\times q -(2) \times p \quad より$
$\quad a(q-p)=aqy$

$\quad y=\cfrac{q-p}{q}=1-\cfrac{p}{q}=1-\cfrac{1}{\tan \theta}=1-\cfrac{1}{\alpha}=\cfrac{\alpha -1}{\alpha}$


$ベクトルの内積のままで計算するか、成分表示で求めるかは解答者次第ですが、$
$この別解のように図形の性質を利用すると計算がかなり楽になります。$

ページの先頭へ↑