バームクーヘン分割による回転体の体積

　

$y\ 軸の回りの回転体の体積を求めるには、y\ 軸に垂直な平面でスライスすると断面は$

$円になるから、円の面積に厚み \ \Delta y \ をかけて、この小円柱を積分して求めます。$

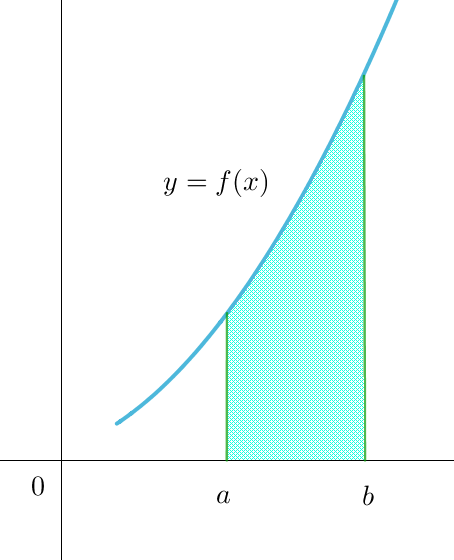
$右図のような曲線 \ y=f(x)\ と \ x\ 軸および直線 \ x=a,\ x=b\ で囲まれた領域をy\ 軸の$

$回りに回転してできる回転体の体積を求めるのにこの方法ではやっかいです。$

$ところが、誰が最初に考えたわかりませんが、バームクーヘン分割といううまい$

$方法があります。$

　
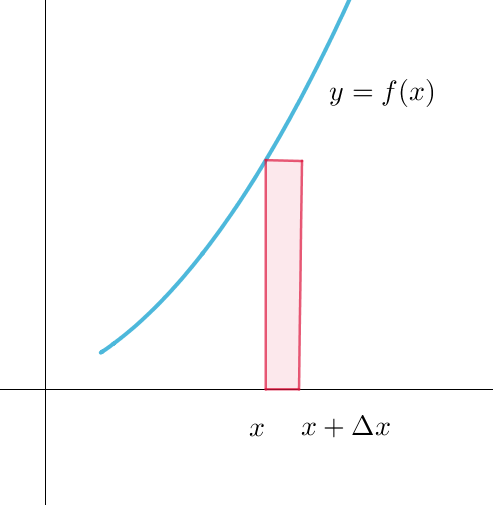
$区間 \ [a,\ b]\ を分割した小区間 \ [x,\ x+\Delta x]\ における曲線下の微小な長方形を$

$y\ 軸の回りに回転してできる厚みのある円筒を集めると求める回転体の体積が$

$得られます。この分割があたかもバームクーヘンのようなイメージであること$

$からこの名前がついています。$

　
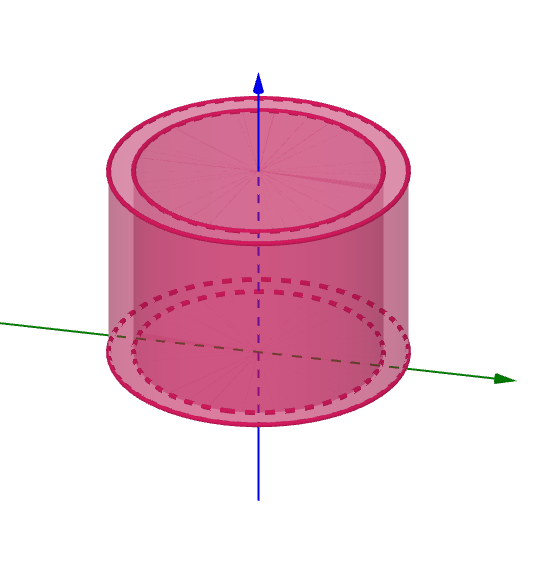
$円筒の円周は、2\pi xで高さはf(x),厚みは\Delta x だから微小体積は$

$\qquad \Delta V=2\pi x \times f(x) \times \Delta x$

$これを区間[a,b]で集めれば求める回転体の体積となるから$

\[V=\int _a^b 2\pi xf(x)dx \]

$バームクーヘン分割による回転体の体積$

$区間 \ [a,\ b]\ で \ f(x) \geqq 0 \ \ とする。曲線 \ y=f(x)\ と \ x\ 軸および直線 \ x=a,\ x=b\ で囲まれた領域を$
$y\ 軸の回りに回転してできる回転体の体積は$
\[\qquad V=2\pi\int _a^bxf(x)dx\]



$例$

　
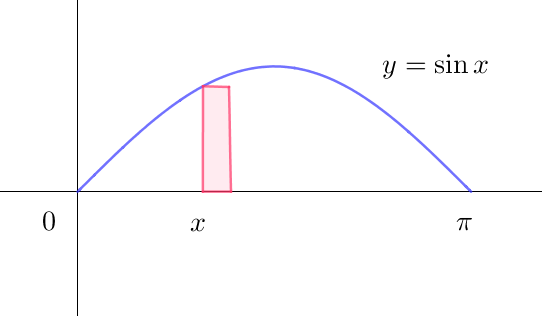
$曲線 \ \ y=\sin x \ \ (0 \leqq x \leqq \pi) \ \ と \ x\ 軸で囲まれた領域を \ y\ 軸の回りに回転して$
$できる回転体の体積$

\begin{eqnarray*} V &=&2\pi\int _0^{\pi} x \sin xdx\\ \\ &=&2\pi\big[-x\cos x\big]_0^{\pi} + 2\pi\int _0^{\pi}\cos x dx\\ \\ &=&2\pi \times \pi + 2\pi \big[\sin x\big]_0^{\pi}\\ \\ &=&2\pi ^2 \end{eqnarray*}
$これを従来の方法で求めると$

　
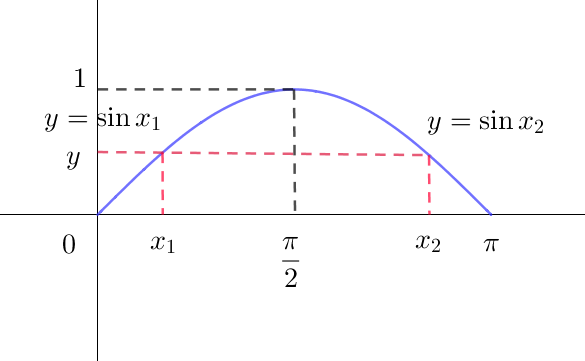
$曲線 \ y=f(x)=\sin x\ \ を$
\[ \hspace{1em} y= \left\{ \begin{array}{l} f(x_1)=\sin x_1 \quad (0 \leqq x_1 \leqq \cfrac{\pi}{2})\\ f(x_2)=\sin x_2 \quad (\cfrac{\pi}{2} \leqq x_2 \leqq \pi)\\ \end{array} \right. \] $とおくと$
\begin{eqnarray*} V &=&\pi\int _0^1 x_2^2dy - \pi \int _0^1x_1^2dy\\ \\ &=&\pi\int _{\pi}^{\scriptsize{\cfrac{\pi}{2}}} x_2^2\cos x_2dx_2 - \pi\int _0^{\scriptsize{\cfrac{\pi}{2}}} x_1^2\cos x_1dx_1 \\ \\ &=&-\pi\int _{\scriptsize{\cfrac{\pi}{2}}}^{\pi} x_2^2\cos x_2dx_2 - \pi\int _0^{\scriptsize{\cfrac{\pi}{2}}} x_1^2\cos x_1dx_1 \\ \\ &=&-\pi\int _0^{\pi} x^2\cos xdx\\ \\ &=&-\pi\big(\big[x^2 \sin x \big]_0^{\pi} -\int _0^{\pi} 2x\sin xdx\big)\\ \\ &=&2\pi\int _0^{\pi} x\sin xdx\\ \end{eqnarray*}
$ここで、バームクーヘン分割による積分に一致しました。$


ページの先頭へ↑



メインメニュー　に戻る