1.ボールも箱も区別する場合
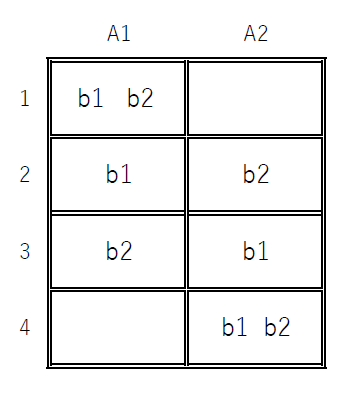
$例1 2個のボールb_1,b_2を2つの箱A_1,A_2に入れる場合$
$ 全事象は、右図のとおりで4通りあるが、そのどれが起こることも$
$同様に確からしいとする。$
$どの箱にもボールが入っているのは右図の(2)(3)の場合だから、その確率は$
$\hspace{2em} P(2,2)=\cfrac{2}{4}=\cfrac{1}{2}$
$例2 3個のボールb_1,b_2,b_3を3つの箱A_1,A_2,A_3に入れる場合$
$全事象は 3^3=27通りで$
$各箱には1個ずつボールが入るから、これはb_1,b_2,b_3の順列であるから$
$\hspace{2em} P(3,3)=\cfrac{3!}{3^3}=\cfrac{2}{9}$
$一般に、ボールの個数m個と箱の個数n個が等しい場合には、$
$\hspace{2em} P(n,n)=\cfrac{n!}{n^n}$
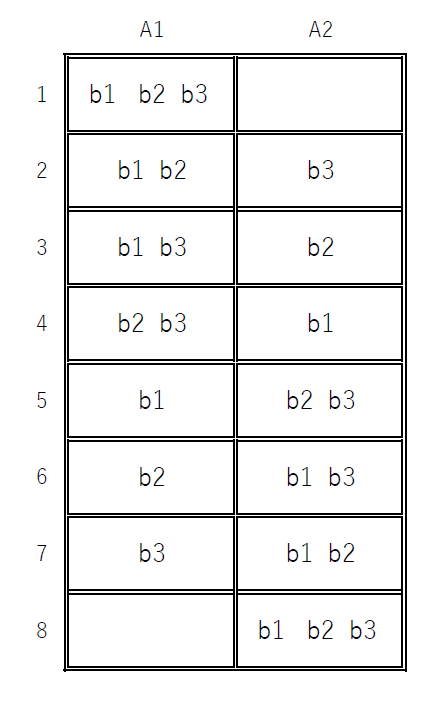
$ 全事象は、右図のとおりで\ 2^3=8 \ 通りあるが、そのどれが$
$起こることも同様に確からしいとする。$
$どの箱にもボールが入っているのは右図の(1)(8)を除く6通りで、その確率は$
$\hspace{2em} P(3,2)=\cfrac{6}{8}=\cfrac{3}{4}$
$なお計算では$
$\hspace{1em}$ (i)$\ A_1に2個、A_2に1個のボールの入れ方は \quad _3C_2=3 通り$
$\hspace{1em}$ (ii)$\ A_1に1個、A_2に2個のボールの入れ方は \quad _3C_1=3 通り$
$したがって、合計6通りと求まります。$
$例4 4個のボールb_1,b_2,b_3,b_4を3つの箱A_1,A_2,A_3に入れる場合$
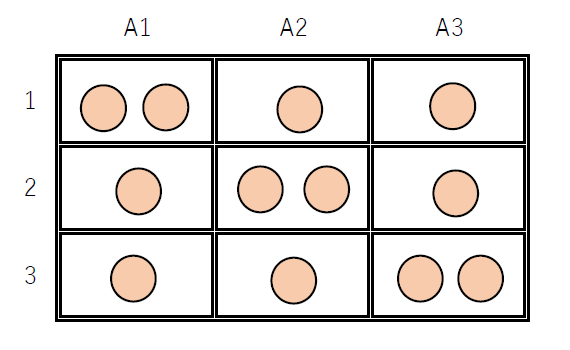
$どの箱にもボールが入っているのは右図の場合です。$
$ボールは区別しますから$
$A_1に2個、A_2に1個、A_3に1個の入れ方は$
$\hspace{2em}_4C_2 \times _2C_1=6 \times 2=12通り$
$A_1に1個、A_2に2個、A_3に1個の入れ方も$
$A_1に1個、A_2に1個、A_3に2個の入れ方も$
$同じだから合計12 \times 3通りの入れ方があります。$
$したがって求める確率は$
$\hspace{2em} P(4,3)=\cfrac{12 \times 3}{3^4}=\cfrac{4}{9}$
$ここまでは教科書や参考書にもあるごく普通の解法です。$
$ボールの個数や箱の個数を増やすとこの解法では困難です。$
$そこで、発想を転換します。$
$具体例で示しましょう。$
$例2別解 3個のボールb_1,b_2,b_3を3つの箱A_1,A_2,A_3に入れる場合において$
(i)$\ \ ある1つの箱にボールが入らない場合$
$箱A_1にボールが入る事象を同じくA_1とする。A_1に入らない場合(A_2,A_3のどちらかに入らない場合も含む)$
$は事象\overline{A_1}と表されるが、そのときA_2,A_3に3個のボールが入るからその確率は$
$\hspace{2em} P(\overline{A_1})=\cfrac{2^3}{3^3}=(1-\cfrac{1}{3})^3$
$ 箱A_2,A_3にボールが入らない場合も全く同様だから$
$\hspace{2em} P(\overline{A_1})=P(\overline{A_2})=P(\overline{A_3})$
$よって、この事象の確率P_1は$
$\hspace{2em} P_1=P(\overline{A_1})+P(\overline{A_2})+P(\overline{A_3})=_3C_1(1-\cfrac{1}{3})^3=\cfrac{8}{9}$
(ii)$\ \ 2つの箱にボールが入らない場合$
$箱A_1とA_2にボールが入らない場合は、箱A_3に3個のボールが入るから、その確率は$
$\hspace{2em} P(\overline{A_1} \cap \overline{A_2})=\cfrac{1}{3^3}=(1-\cfrac{2}{3})^3$
$箱A_2とA_3,箱A_3とA_1にボールが入らない場合も全く同様だから$
$\hspace{2em} P(\overline{A_1} \cap \overline{A_2})=P(\overline{A_2} \cap \overline{A_3})=P(\overline{A_3} \cap \overline{A_1})$
$よって、この事象の確率P_2は$
$\hspace{2em} P_2=P(\overline{A_1} \cap \overline{A_2})+P(\overline{A_2} \cap \overline{A_3})+P(\overline{A_3} \cap \overline{A_1})=_3C_2(1-\cfrac{2}{3})^3$
(iii)$\ \ 3つの箱にボールが入らない場合$
$このような事象はありえないので(空事象といっていいが)、その確率 \ P_3 \ は \ P_3=0 \ であるが、$
(i),(ii)$にならって$
$\hspace{2em} P_3=P(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3})=_3C_3(1-\cfrac{3}{3})^3$
$とします。$
(i)(ii)(iii)$より、3つの箱のいずれかにボールが入らない確率は$
$\hspace{3em}P(\overline{A_1} \cup \overline{A_2} \cup \overline{A_3})$
\begin{eqnarray*} &=&P(\overline{A_1})+P(\overline{A_2})+P(\overline{A_3})-P(\overline{A_1} \cap \overline{A_2}) -P(\overline{A_2} \cap \overline{A_3})-P(\overline{A_3} \cap \overline{A_1}) +P(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3})\hspace{5em}\hspace{5em}\\ &=&P_1-P_2+P_3\\ &=&\sum_{k=1}^3(-1)^{k-1}\ _3C_k(1-\cfrac{k}{3})^3 \\ \end{eqnarray*} $したがって、どの箱にも少なくとも1個のボールが入る確率は$
\begin{eqnarray*} P(3,3) &=&P(A_1 \cap A_2 \cap A_3)\\ &=&=1-P(\overline{A_1 \cap A_2 \cap A_3})\\ &=&1-P(\overline{A_1} \cup \overline{A_2} \cup \overline{A_3})\\ &=&1-\sum_{k=1}^3(-1)^{k-1}\ _3C_k(1-\cfrac{k}{3})^3\\ &=&\sum_{k=0}^3(-1)^{k}\ _3C_k(1-\cfrac{k}{3})^3 \hspace{3em} (k=0 のとき(-1)^0\ _3C_0(1-\cfrac{0}{3})^3=1だから)\\ &=&1-\cfrac{8}{9}+\cfrac{1}{9}-0\\ &=&\cfrac{2}{9}\\ \end{eqnarray*}
$例2の解法と比べると、かなり込み入っているように見えますが、この方法は一般化できるのです。$
$ボールの個数をm個とした場合は$
\[\hspace{2em} P(m,3)=\sum_{k=0}^3(-1)^{k}\ _3C_k(1-\cfrac{k}{3})^m\] $で求まることはすぐわかるでしょう。$
$例4別解 4個のボールb_1,b_2,b_3,b_4を3つの箱A_1,A_2,A_3に入れる場合$
$ をこの公式で計算してみましょう。$
$P(4,3)=1-_3C_1(1-\cfrac{1}{3})^4+_3C_2(1-\cfrac{2}{3})^4-_3C_3(1-\cfrac{3}{3})^4$
$\hspace{3em} =1-3 \times \cfrac{2^4}{3^4}+3 \times \cfrac{1}{3^4}-0$
$\hspace{3em} =\cfrac{4}{9}$
$となって解は一致するのがわかります。$
$それでは箱の個数を増やすとどうなるでしょうか。$
$例5 4個のボールb_1,b_2,b_3,b_4を4つの箱A_1,A_2,A_3,A_4に入れる場合$
(i)$ 1つの箱にボールが入らない場合$
$箱A_1にボールが入らない場合(A_2,A_3,A_4のどれかにボールが入らない場合も含む)は \ A_2,A_3,A_4に$
$4個のボールが入るから$
$\hspace{2em} P(\overline{A_1})=\cfrac{3^4}{4^4}=(1-\cfrac{1}{4})^4$
$箱A_2,A_3,A_4にボールが入らない場合も全く同様だから$
$\hspace{2em} P(\overline{A_1})=P(\overline{A_2})=P(\overline{A_3})=P(\overline{A_4})$
$よって、この事象の確率P_1は$
$\hspace{2em} P_1=P(\overline{A_1})+P(\overline{A_2})+P(\overline{A_3})+P(\overline{A_4}) =_4C_1(1-\cfrac{1}{4})^4$
(ii)$ 2つの箱にボールが入らない場合$
$箱A_1とA_2にボールが入らない場合は、箱A_3,A_4に4個のボールが入るから、その確率は$
$\hspace{2em} P(\overline{A_1} \cap \overline{A_2})=\cfrac{2^4}{4^4}=(1-\cfrac{2}{4})^4$
$箱A_1とA_3,箱A_1とA_4,箱A_2とA_3,箱A_2とA_4,箱A_3とA_4 にボールが入らない場合も全く同様だから$
$\hspace{1em} P(\overline{A_1} \cap \overline{A_2})= P(\overline{A_1} \cap \overline{A_3}) = P(\overline{A_1} \cap \overline{A_4})=P(\overline{A_2} \cap \overline{A_3}) = P(\overline{A_2} \cap \overline{A_4})=P(\overline{A_3} \cap \overline{A_4})$
$よって、この事象の確率P_2は$
$\hspace{2em} P_2=_4C_2(1-\cfrac{2}{4})^4$
(iii)$ 3つの箱にボールが入らない場合$
$箱A_1,A_2,A_3にボールが入らない場合は、箱A_4に4個のボールが入るから、その確率は$
$\hspace{2em} P(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3})=\cfrac{1}{4^4}=(1-\cfrac{3}{4})^4$
$箱A_1,A_2,A_4,箱A_1,A_3,A_4,箱A_2,A_3,A_4 にボールが入らない場合も全く同様だから$
$\hspace{2em} P(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3}) = P(\overline{A_1} \cap \overline{A_2} \cap \overline{A_4}) = P(\overline{A_1} \cap \overline{A_3} \cap \overline{A_4}) = P(\overline{A_2} \cap \overline{A_3} \cap \overline{A_4})$
$よって、この事象の確率P_3は$
$\hspace{2em} P_3=_4C_3(1-\cfrac{3}{4})^4$
(iv)$ 4つの箱にボールが入らない場合$
$このような事象はありえないので(空事象といっていいが)、その確率 \ P_4 \ は \ P_4=0 \ であるが、$
(i),(ii),(iii)$にならって$
$\hspace{2em} P_4=P(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3} \cap \overline{A_3}) =_4C_4(1-\cfrac{4}{4})^4$
$とします。$
$ここで、4つの事象の和事象の確率を求めるために、4つの集合の和集合の要素の個数を求めなくてはなりません。それは$
$|A \cup B \cup C \cup D|$
$=|A|+|B|+|C|+|D|-|A\cap B|-|A \cap C|-|A \cap D|-|B\cap C| -|B\cap D|-|C \cap D|$
$\hspace{3em} +|A\cap B\cap C|+|A\cap B\cap D|+|A\cap C\cap D|+|B\cap C\cap D| -|A\cap B\cap C \cap D|$
$この両辺を全事象の個数で割れば確率の公式となりますので$
(i)(ii)(iii)(iv)$より、4つの箱のいずれかにボールが入らない確率は$
$\hspace{2em}P(\overline{A_1} \cup \overline{A_2} \cup \overline{A_3} \cup \overline{A_4})$
$\hspace{2em}=P(\overline{A_1})+P(\overline{A_2})+P(\overline{A_3})+P(\overline{A_4}) -P(\overline{A_1} \cap \overline{A_2}) -P(\overline{A_1} \cap \overline{A_3}) -P(\overline{A_1} \cap \overline{A_4})$
$\hspace{4em} -P(\overline{A_2} \cap \overline{A_3}) -P(\overline{A_2} \cap \overline{A_4}) -P(\overline{A_3} \cap \overline{A_4}) +P(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3}) +P(\overline{A_1} \cap \overline{A_2} \cap \overline{A_4})$
$\hspace{4em} +P(\overline{A_1} \cap \overline{A_3} \cap \overline{A_4}) +P(\overline{A_2} \cap \overline{A_3} \cap \overline{A_4}) -P(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3} \cap \overline{A_4})$
$\hspace{2em}=P_1-P_2+P_3-P_4$
\[=\sum_{k=1}^4(-1)^{k-1}\ _4C_k(1-\cfrac{k}{4})^4 \] $したがって、どの箱にも少なくとも1個のボールが入る確率は$
\begin{eqnarray*} \hspace{2em}P(4,4) &=&P(A_1 \cap A_2 \cap A_3 \cap A_4)\\ &=&1-P(\overline{A_1 \cap A_2 \cap A_3 \cap A_4})\\ &=&1-P(\overline{A_1} \cup \overline{A_2} \cup \overline{A_3} \cup \overline{A_4})\\ &=&1-\sum_{k=1}^4(-1)^{k-1}\ _4C_k(1-\cfrac{k}{4})^4\\ &=&\sum_{k=0}^4(-1)^{k}\ _4C_k(1-\cfrac{k}{4})^4 \hspace{3em} (k=0 のとき(-1)^0\ _4C_0(1-\cfrac{0}{4})^4=1だから)\\ &=&1-\cfrac{81}{64}+\cfrac{24}{64}-\cfrac{1}{64}+0\\ &=&\cfrac{3}{32}\\ \end{eqnarray*}
$一般に、m個のボールb_1,b_2,\cdots , b_mをn個の箱A_1,A_2,\cdots , A_nに入れる場合です。$
$ただし、n < m \ とします。$
$これには、n個の集合の和集合の要素の個数$
$n個の集合A_1,A_2,\cdots , A_nの和集合 \bigcup_{i=1}^{n}{ A_i}の要素の個数は$
\[|\bigcup_{i=1}^{n}{ A_i}|=\sum _{i=1}^{n}|A_i|- \sum_{i < j}^{n}|A_i \cap A_j|
+\sum_{i < j < k}^{n}|A_i \cap A_j \cap A_k|- \cdots +(-1)^{n-1}|A_1 \cap A_2 \cap \cdots \cap A_n|\]
$n個のどの箱にも少なくとも1個のボールが入る確率は$
\begin{eqnarray*} \hspace{2em}P(m,n) &=&P(A_1 \cap A_2 \cap \cdots \cap A_n)\\ &=&1-P(\overline{A_1 \cap A_2 \cap \cdots \cap A_n})\\ &=&1-P(\overline{A_1} \cup \overline{A_2} \cup \cdots \cup \overline{A_n})\\ &=&\sum_{k=0}^n(-1)^{k}\ _nC_k(1-\cfrac{k}{n})^m\\ \end{eqnarray*}
$になることは簡単に類推できるでしょう。$
$\qquad m個のボールをn個の箱に入れるとき、どの箱にも少なくとも1個のボールが入る確率は$
\[\qquad P(m,n)=\sum_{k=0}^n(-1)^{k}\ _nC_k(1-\cfrac{k}{n})^m \qquad ただし、n < m \]
$最後に、m個のボールb_1,b_2,\cdots , b_mをn個の箱A_1,A_2,\cdots , A_nに入れるとき \ r個の箱にボールが$
$1個も入らない場合です。ただし r < n < m \ とします。$
$ボールが入らない箱の選び方は _nC_r 通り$
$残り (n-r)個の箱にボールを入れればよいから$
\[\hspace{2em}P(m,n,r) =_nC_r \times \sum_{k=0}^{n-r}(-1)^{k}\ _{n-r}C_k(1-\cfrac{k}{n-r})^m\] $と求まります。$
ボールの分配 に戻る
メインメニュー に戻る