MY MATH NOTE

$連続な極方程式 \ \ r=r(\theta) \ \ (\alpha \leqq \theta \leqq \beta) \ \ で表される曲線の面積は$
\[\hspace{3em} S=\cfrac{1}{2}\int _{\alpha}^{\beta} r^2d\theta\]

　
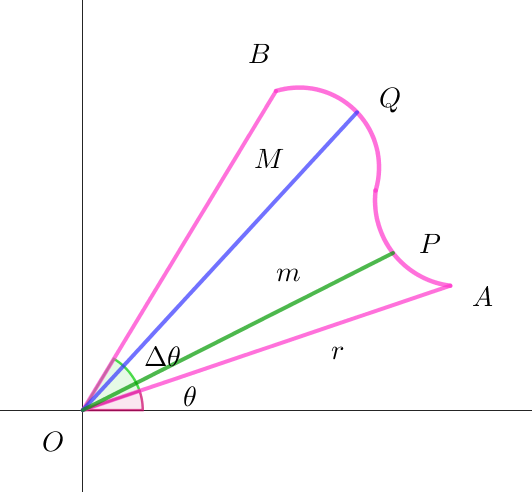
$(証明)$

$半径 \ a,中心角 \ \theta \ の扇形の面積は \quad \cfrac{1}{2}a^2\theta \quad だから$

$微小区間 \ \ \theta \leqq t \leqq \theta +\Delta \theta \ \ での \ r\ の最小値を \ m,最大小値を \ M\ とすると$

$この区間の面積 \ \ \Delta Sは$

$\quad \cfrac{1}{2}m^2\Delta \theta \leqq \Delta S \leqq \cfrac{1}{2}M^2\Delta \theta$

$\quad \cfrac{1}{2}m^2 \leqq \cfrac{\Delta S}{\Delta \theta} \leqq \cfrac{1}{2}M^2$

$\Delta \theta \longrightarrow 0 \quad とすると \quad m \longrightarrow r ,\quad M \longrightarrow r \quad だから$

$はさみ打ちの原理により \quad \cfrac{dS}{d\theta}=\cfrac{1}{2}r^2$

\[\qquad \therefore \ \ S=\cfrac{1}{2} \int _{\alpha}^{\beta} r^2 d\theta\]

ページの先頭へ↑