$4\ 葉形と \ 3\ 葉形$
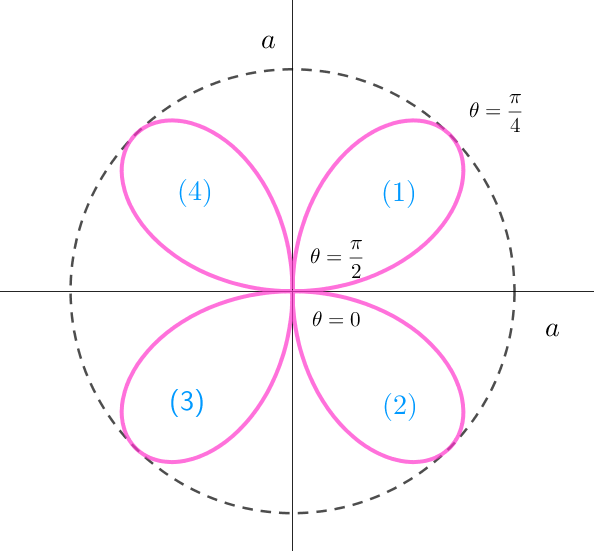
$極座標で \ \ r=a\sin 2 \theta \ \ と表される図形を4葉形といいます。$
$\qquad 詳しくは($4葉形と3葉形$)をご覧ください。$
$この4枚の葉の面積を求めてみましょう。対称性は明らかだから$
\begin{eqnarray*} S &=&4 \times \cfrac{1}{2} \int _0^{\scriptsize{\cfrac{\pi}{2}}} r^2 d\theta\\ \\ &=&2 \int _0^{\scriptsize{\cfrac{\pi}{2}}} a^2\sin ^2 2\theta d\theta\\ \\ &=&2a^2 \int _0^{\scriptsize{\cfrac{\pi}{2}}} \cfrac{1-\cos 4\theta}{2} d\theta\\ \\ &=&a^2 \big[\theta -\cfrac{\sin 4\theta}{4}\big] _0^{\scriptsize{\cfrac{\pi}{2}}}\\ \\ &=&\cfrac{\pi}{2} a^2 \end{eqnarray*}
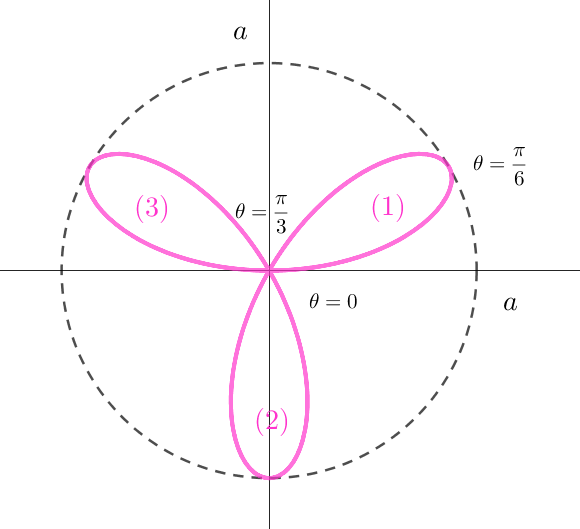
$極座標で \ \ r=a\sin 3 \theta \ \ と表される図形を3葉形といいます。$
$\qquad 詳しくは($4葉形と3葉形$)をご覧ください。$
$この3枚の葉の面積を求めてみましょう。対称性は明らかだから$
\begin{eqnarray*} S &=&3 \times \cfrac{1}{2} \int _0^{\scriptsize{\cfrac{\pi}{3}}} r^2 d\theta\\ \\ &=&\cfrac{3}{2} \int _0^{\scriptsize{\cfrac{\pi}{3}}} a^2\sin ^2 3\theta d\theta\\ \\ &=&\cfrac{3}{2}a^2 \int _0^{\scriptsize{\cfrac{\pi}{3}}} \cfrac{1-\cos 6\theta}{2} d\theta\\ \\ &=&\cfrac{3}{4}a^2 \big[\theta -\cfrac{\sin 6\theta}{6}\big] _0^{\scriptsize{\cfrac{\pi}{3}}}\\ \\ &=&\cfrac{\pi}{4} a^2 \end{eqnarray*}
$(3)\quad n葉形$
$\hspace{8em}n\ が偶数のとき \hspace{18em}n\ が奇数のとき$
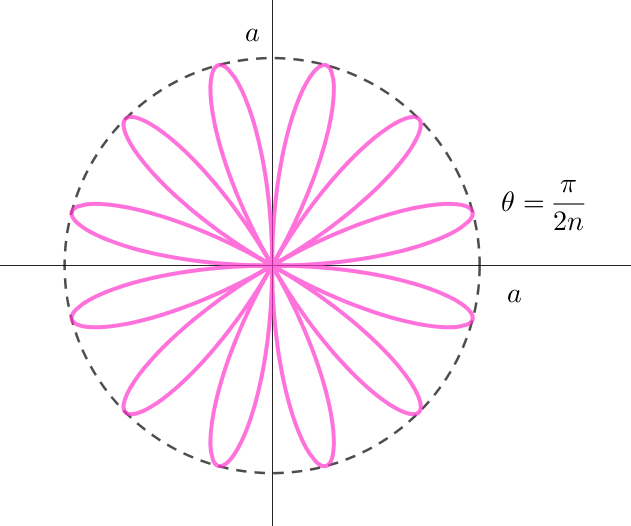
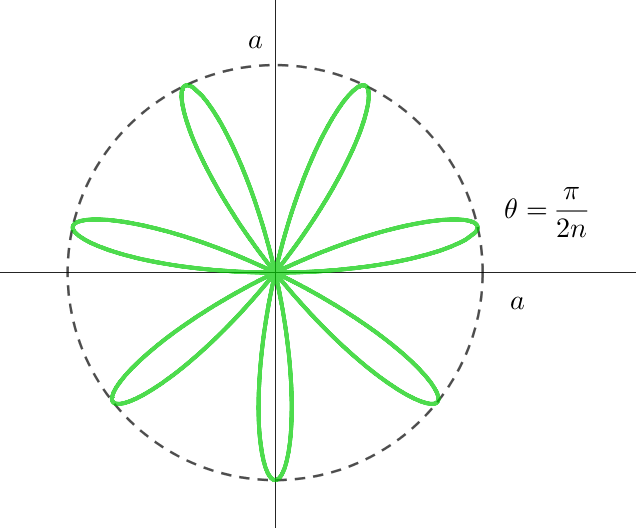
$\sin n\theta=0 \quad となるのは \quad n\theta=k\pi \quad \therefore \ \ \theta =\cfrac{k}{n}\pi$
(i)$\ \ nが偶数のとき$
$\quad 合同な葉は \ 2n\ 枚あるから$
\begin{eqnarray*} \quad S &=&2n \times \cfrac{1}{2} \int _0^{\scriptsize{\cfrac{\pi}{n}}} r^2 d\theta\\ \\ &=&n \int _0^{\scriptsize{\cfrac{\pi}{n}}} a^2\sin ^2 n\theta d\theta\\ \\ &=&na^2 \int _0^{\scriptsize{\cfrac{\pi}{n}}} \cfrac{1-\cos 2n\theta}{2} d\theta\\ \\ &=&\cfrac{n}{2}a^2 \big[\theta -\cfrac{\sin 2n\theta}{2n}\big] _0^{\scriptsize{\cfrac{\pi}{n}}}\\ \\ &=&\cfrac{n}{2}a^2 \times \cfrac{\pi}{n}\\ \\ &=&\cfrac{\pi}{2} a^2 \end{eqnarray*}
$\quad 面積は \ n\ によらず一定であることがわかりました。$
(ii)$\ \ nが奇数のとき$
$\quad 合同な葉は \ n\ 枚あるから$
\[\quad S=n \times \cfrac{1}{2} \int _0^{\scriptsize{\cfrac{\pi}{n}}} r^2 d\theta=\cfrac{\pi}{4} a^2\]
極座標表示による曲線の囲む面積
メインメニュー に戻る