MY MATH NOTE

　
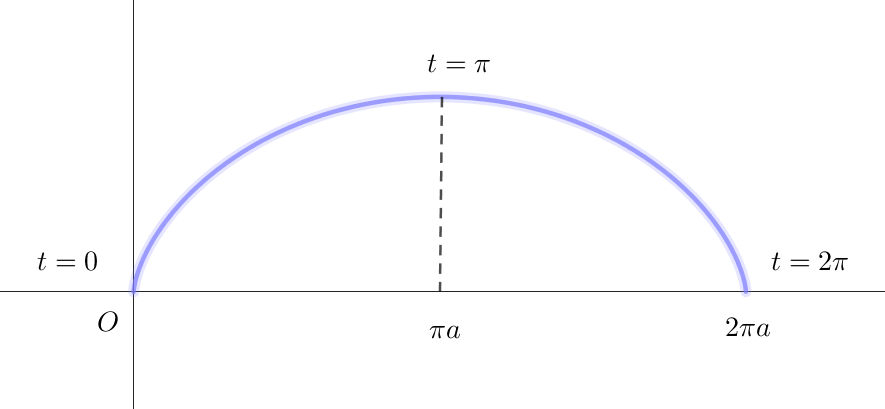
$x=a(t-\sin t),\quad y=a(1- \cos t) \quad で表される曲線をサイクロイド$
$といいます。$

$\qquad 詳しくは($サイクロイド$)をご覧ください。$

$この図形の囲む面積 \ S\ を求めてみましょう。$
\begin{eqnarray*} S &=&\int _0^{2\pi a} ydx\\ \\ &=&\int _0 ^{2\pi} a(1-\cos t) \cdot a(1-\cos t)dt\\ \\ &=&a^2 \int _0 ^{2\pi} (1-\cos t)^2 dt \hspace{3em} (\cos t=1-2\sin ^2 \cfrac{t}{2} \quad だから)\\ \\ &=&a^2 \int _0 ^{2\pi} 4\sin ^4 \cfrac{t}{2} dt \hspace{4em} (\cfrac{t}{2}=u \quad とおくと \quad dt=2du)\\ \\ &=&4a^2 \int _0 ^{\pi} \sin ^4 u \cdot 2du \\ \\ &=&8a^2 \int _0 ^{\pi} \sin ^4 u du \\ \\ &=&8a^2 \big(\int _0 ^{\scriptsize{\cfrac{\pi}{2}}} \sin ^4 u du+ \int _{\scriptsize{\cfrac{\pi}{2}}}^{\pi} \sin ^4 u du \big)\\ \end{eqnarray*} \[\qquad 積分第2項で \quad \pi -u =s \quad とおくと \quad du=-ds \qquad \begin{array}{c|c} u & \scriptsize{\cfrac{\pi}{2}} \ \ \rightarrow \normalsize{\pi} \\ \hline s & \scriptsize{\cfrac{\pi}{2}} \ \ \rightarrow \normalsize{0} \\ \end{array} \quad だから \] \[第2項=\int _{\scriptsize{\cfrac{\pi}{2}}}^0 \sin ^4 (\pi -s)(-ds)=\int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin ^4 s ds\] $よって$

\begin{eqnarray*} S &=&16a^2 \int _0 ^{\scriptsize{\cfrac{\pi}{2}}} \sin ^4 u du\\ \\ &=&16a^2 \cdot \cfrac{3}{4} \cdot \cfrac{1}{2} \cdot \cfrac{\pi}{2}\\ \\ &=&3\pi a^2 \end{eqnarray*} $\qquad この定積分の値の求め方は \ \ $$\int_{0}^{\scriptsize{\cfrac{\pi}{2}}}\sin^m x \cos ^n xdx$ $\ \ をご覧ください$


$なお、この定積分は次のように直接求めることもできます。$

\begin{eqnarray*} S &=&a^2 \int _0 ^{2\pi} (1-\cos t)^2 dt \\ \\ &=&a^2 \int _0 ^{2\pi} (1-2\cos t +\cos ^2 t)dt \\ \\ &=&a^2 \int _0 ^{2\pi} (1-2\cos t +\cfrac{1+\cos 2t}{2})dt \\ \\ &=&a^2 \big[\cfrac{3}{2}t-2\sin t +\cfrac{\sin 2t}{4}\big]_0^{2\pi}\\ \\ &=&3\pi a^2 \end{eqnarray*}

ページの先頭へ↑