MY MATH NOTE

　
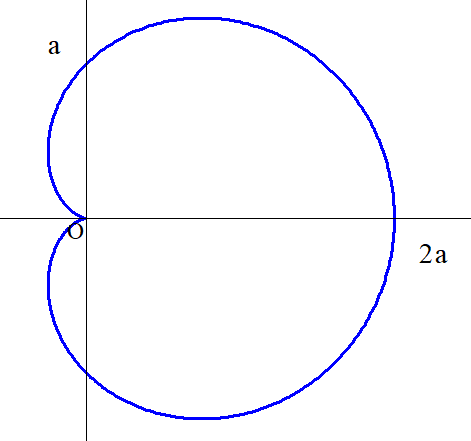
$極座標で \ \ r=a(1+\cos \theta)\ \ と表される図形をカージオイドといいます。$

$\qquad 詳しくは($カージオイド$)をご覧ください。$

$この図形の囲む領域の面積を求めてみましょう。対称性は明らかだから$
\begin{eqnarray*} S &=&2 \times \cfrac{1}{2} \int _0^{\pi} r^2 d\theta\\ \\ &=&\int _0^{\pi} a^2(1+\cos \theta )^2 d\theta \hspace{3em} (\cos \theta=2\cos ^2 \cfrac{\theta}{2}-1 \quad だから)\\ \\ &=&a^2 \int _0 ^{\pi} 4\cos ^4 \cfrac{\theta}{2} d\theta \hspace{4em} (\cfrac{\theta}{2}=t \quad とおくと \quad d\theta=2dt)\\ \\ &=&4a^2 \int _0 ^{\scriptsize{\cfrac{\pi}{2}}} \cos ^4 t \cdot 2dt \\ \\ &=&8a^2 \cdot \cfrac{3}{4} \cdot \cfrac{1}{2} \cdot \cfrac{\pi}{2}\\ \\ &=&\cfrac{3}{2}\pi a^2 \end{eqnarray*} $\qquad この定積分の値の求め方は \ \ $$\int_{0}^{\scriptsize{\cfrac{\pi}{2}}}\sin^m x \cos ^n xdx$ $\ \ をご覧ください$


$なお、この定積分は次のように直接求めることもできます。$

\begin{eqnarray*} S &=&a^2 \int _0 ^{\pi} (1+\cos \theta)^2 d\theta \\ \\ &=&a^2 \int _0 ^{\pi} (1+2\cos \theta +\cos ^2 \theta)d\theta \\ \\ &=&a^2 \int _0 ^{\pi} (1+2\cos \theta +\cfrac{1+\cos 2\theta}{2})d\theta \\ \\ &=&a^2 \big[\cfrac{3}{2}\theta+2\sin \theta +\cfrac{\sin 2\theta}{4}\big]_0^{\pi}\\ \\ &=&\cfrac{3}{2}\pi a^2 \end{eqnarray*}

ページの先頭へ↑