フーリェ級数の周期の一般化
$区間 \ [-T,\ T]\ で表された周期 \ 2T\ の区分的になめらかな周期関数のフーリェ級数を考えましょう。$
$-\pi \leqq t < \pi \ \ で定義された関数 \ f(t)\ に対して、t=\cfrac{\pi}{T}x \ \ と変換した関数を \ f^*(x)\ とすると$
\[f^*(x)=f(t)=f(\cfrac{\pi}{T}x) \qquad dt=\cfrac{\pi}{T}dx \qquad \quad \begin{array}{c|c} t & -\pi\ \ \rightarrow \pi \\ \hline x & -T \rightarrow T \\ \end{array} \]
$よって$
\[f(t)=\cfrac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos nt+b_n\sin nt) \quad は \quad f^*(x)=\cfrac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos \cfrac{n\pi}{T}x + b_n\sin \cfrac{n\pi}{T}x)\] $ここに$
\[a_0=\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(t)dt=\cfrac{1}{\pi}\int_{-T}^T f^*(x)\cfrac{\pi}{T}dx=\cfrac{1}{T}\int_{-T}^T f^*(x)dx\]
\[a_n=\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(t)\cos ntdt=\cfrac{1}{\pi}\int_{-T}^T f^*(x)\cos \cfrac{n\pi}{T}x \cdot \cfrac{\pi}{T}dx=\cfrac{1}{T}\int_{-T}^T f^*(x)\cos \cfrac{n\pi}{T}xdx\]
\[b_n=\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(t)\sin ntdt=\cfrac{1}{\pi}\int_{-T}^T f^*(x)\sin \cfrac{n\pi}{T}x \cdot \cfrac{\pi}{T}dx=\cfrac{1}{T}\int_{-T}^T f^*(x)\sin \cfrac{n\pi}{T}xdx\]
$あらためて、f^*(x) \ を \ f(x)\ と書き直すとフーリェ級数は$
\[f(x)=\cfrac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos \cfrac{n\pi}{T}x + b_n\sin \cfrac{n\pi}{T}x) \] $ただし$
\[a_n=\cfrac{1}{T}\int_{-T}^T f(x)\cos \cfrac{n\pi}{T}xdx, \qquad b_n=\cfrac{1}{T}\int_{-T}^T f(x)\sin \cfrac{n\pi}{T}xdx\]
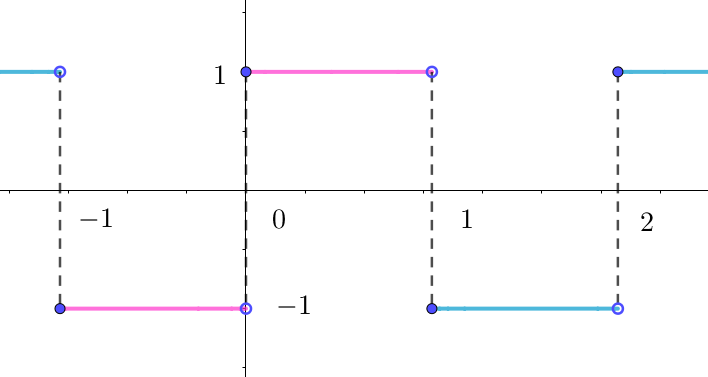
$例 \quad 右図のグラフのような「矩形波」のフーリェ級数展開を$
$\qquad 求めてみましょう。$
\[
f(x)=
\hspace{1em}
\left\{ \begin{array}{l}
-1 \quad (-1 \leqq x < 0)\\
1 \qquad (0 \leqq x <1)\\
\end{array} \right.
\]
$\quad f(x)\ は周期 \ 2 \ の周期関数だから \quad 2T=2 \quad より \quad T=1$
$\quad f(x)\ は奇関数だから \quad a_0=0,\quad a_n=0$
\begin{eqnarray*}
b_n
&=&\int_{-1}^1 f(x)\sin n\pi xdx\\
&=&\int_{-1}^0 (-1)\sin n\pi xdx + \int_0^1\sin n\pi xdx\\
&=&\cfrac{1}{n\pi}\big[\cos n\pi x\big]_{-1}^0 - \cfrac{1}{n\pi}\big[\cos n\pi x\big]_0^1\\
&=&\cfrac{2}{n\pi}(1-\cos n\pi)\\
&=&\left\{ \begin{array}{l}
\cfrac{4}{n\pi} \hspace{4em}(n=2k-1)\\
0 \hspace{5em}(n=2k)\\
\end{array} \right.
\end{eqnarray*}
$したがって$
\begin{eqnarray*}
f(x)
&=&\sum_{n=1}^\infty b_n\sin n\pi x\\
&=&\sum_{k=1}^\infty \cfrac{4}{(2k-1)\pi}\sin (2k-1)\pi x\\
&=&\cfrac{4}{\pi}(\sin \pi x +\cfrac{1}{3}\sin 3\pi x +\cfrac{1}{5}\sin 5\pi x + \cdots )
\end{eqnarray*}
フーリェ級数メニュー に戻る
メインメニュー に戻る