フーリェ級数の収束性
1 区分的になめらかな曲線
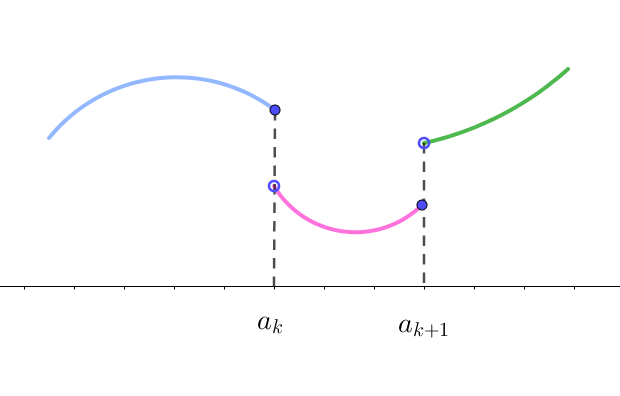
$区間 \ [a,\ b]\ で定義された関数 \ f(x)\ が有限個の点で不連続、すなわち$
\[\lim _{\varepsilon \rightarrow +0} f(a_k-\varepsilon)=f(a_k-0)\]
\[\lim _{\varepsilon \rightarrow +0} f(a_k+\varepsilon)=f(a_k+0)\]
$がともに存在し、f(a_k-0) \ne f(a_k+0)$
$かつ \ f(x)\ の導関数が、小区間 \ [a_k.\ a_{k+1}]\ で連続で有限な極限値$
\[\lim _{\varepsilon \rightarrow +0} f'(a_k+\varepsilon)=f'(a_k+0),\qquad\lim _{\varepsilon \rightarrow +0}f'(a_{k+1} -\varepsilon) =f'(a_{k+1}-0)\]
$がともに存在する。$
$これらがなりたつとき、f(x)\ は区間 \ [a,\ b]\ で区分的になめらか、あるいは有界変分であるともいいます。$
2 ディレクレ核
$\quad 周期 \ 2\pi\ の周期関数 \ f(x)\ のフーリェ級数の第 \ n\ 部分和は$
\begin{eqnarray*} S_n(x) &=&\cfrac{a_0}{2}+\sum_{k=1}^n (a_k\cos kx+b_k\sin kx)\\ &=&\cfrac{1}{2\pi}\int _{-\pi}^{\pi}f(t)dt + \sum_{k=1}^n \Big\{\big (\cfrac{1}{\pi}\int _{-\pi}^{\pi} f(t)\cos kt dt\big)\cos kx + \big(\cfrac{1}{\pi}\int _{-\pi}^{\pi} f(t)\sin kt dt \big)\sin kx \Big\}\\ &=&\cfrac{1}{2\pi}\int _{-\pi}^{\pi}f(t)dt + \cfrac{1}{\pi}\sum_{k=1}^n \int _{-\pi}^{\pi} (f(t)\cos kt\cos kx + f(t)\sin kt \sin kx)dt\\ &=&\cfrac{1}{2\pi}\int _{-\pi}^{\pi}f(t)dt + \cfrac{1}{\pi}\sum_{k=1}^n \int _{-\pi}^{\pi} f(t)\cos k(t-x)dt\\ &=&\cfrac{1}{\pi}\int _{-\pi}^{\pi}f(t)\Big\{\cfrac{1}{2}+\sum_{k=1}^n \cos k(t-x)\Big\}dt\\ \end{eqnarray*} \[t-x=u \quad とおくと \quad dt=du \qquad \begin{array}{c|c} t & -\pi \hspace{1em} \rightarrow \pi\\ \hline u & \ -\pi-x \rightarrow \pi - x\\ \end{array} \] \[S_n(x)=\cfrac{1}{\pi}\int _{-\pi -x}^{\pi -x }f(u+x)\big(\cfrac{1}{2}+\sum_{k=1}^n \cos ku\big)du\]
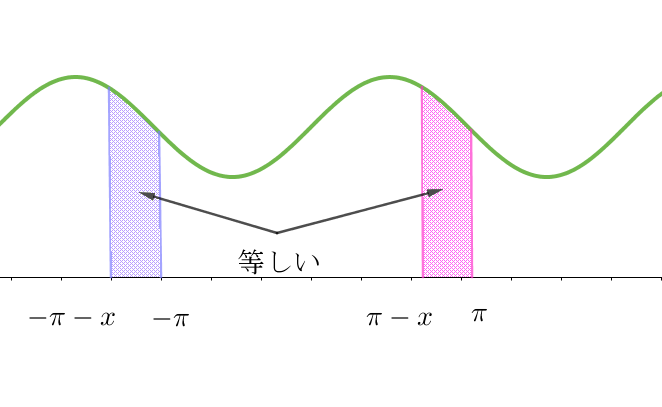
$\quad f(u+x),\ \ \cos ku \quad は周期 \ 2\pi \ の周期関数だから$
\[S_n(x)=\cfrac{1}{\pi}\int _{-\pi}^{\pi}f(u+x)\big(\cfrac{1}{2}+\sum_{k=1}^n \cos ku\big)du\]
\[ここで D(u)=\cfrac{1}{2}+\sum_{k=1}^n \cos ku \]
$\quad をディレクレ核といいますが、その性質を調べましょう。$
$\qquad (1)\ \ D(-u)=D(u) \quad すなわち \quad D(u)\ \ は偶関数$
\[\hspace{3em} D(-u)=\cfrac{1}{2}+\sum_{k=1}^n \cos k(-u)=\cfrac{1}{2}+\sum_{k=1}^n \cos ku=D(u)\]
\[(2)\ \ \int _{-\pi}^{\pi}D(u)du=\pi\]
\[\hspace{3em} \int _{-\pi}^{\pi} \big(\cfrac{1}{2}+\sum_{k=1}^n \cos ku\big)du=\big[\cfrac{1}{2}u + \cfrac{1}{k}\sum_{k=1}^n \sin ku\big]_{-\pi}^{\pi}=\pi\]
$ \qquad (3)\ \ D(u)=\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}$
$\hspace{3em} これについては \quad $ $\sum_{k=1}^n \sin kx ,\quad \sum_{k=1}^n \cos kx $$ \quad の \ (2)\ 余弦の和 \ (1)\ をご覧ください。$
3 収束性
$定理 \qquad 2\pi \ \ を周期とする関数 \ f(x)\ は区分的になめらかとする。$
$\hspace{5em} n \longrightarrow \infty \quad のとき \quad S_n(x) \longrightarrow \cfrac{1}{2}\{f(x+0)+f(x-0)\} $
$(証明)$
$(1)\ \ f(x)\ が \ x=x_0\ で連続な場合$
$\qquad \cfrac{1}{2}\{f(x_0+0)+f(x_0-0)\}=f(x_0)$
\[S_n(x_0)=\cfrac{1}{\pi}\int _{-\pi}^{\pi}f(u+x_0)D(u)du=\cfrac{1}{\pi}\int _{-\pi}^{\pi}f(u+x_0)\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}\] \[\cfrac{1}{\pi}\int _{-\pi}^{\pi}D(u)du=\cfrac{1}{\pi}\int _{-\pi}^{\pi}\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du=1\] $\quad より$
\begin{eqnarray*} & &S_n(x_0)-f(x_0)\\ &=&\cfrac{1}{\pi}\int _{-\pi}^{\pi}f(u+x_0)\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du - 1 \times f(x_0)\\ \\ &=&\cfrac{1}{\pi}\int _{-\pi}^{\pi}f(u+x_0)\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du - \cfrac{1}{\pi}\int _{-\pi}^{\pi}\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du \times f(x_0)\\ \\ &=&\cfrac{1}{\pi}\int _{-\pi}^{\pi}\big\{f(u+x_0)-f(x_0)\big\}\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du \\ \\ &=&\cfrac{1}{\pi}\int _{-\pi}^{\pi}\cfrac{f(u+x_0)-f(x_0)}{2\sin \dfrac{u}{2}} \cdot \sin (n+\dfrac{1}{2})u du \\ \end{eqnarray*}
$\qquad g(u)=\cfrac{f(u+x_0)-f(x_0)}{2\sin \dfrac{u}{2}} \quad は \quad u \longrightarrow 0 \quad とすると不定形であるが \quad g(u)=\cfrac{f(u+x_0)-f(x_0)}{u} \cdot \cfrac{\dfrac{u}{2}}{\sin \dfrac{u}{2}} \quad より$
\[f(x)\ が区分的になめらかだから \quad \lim _{u \rightarrow 0} \cfrac{f(u+x_0)-f(x_0)}{u}=f'(x_0) \quad は存在する。\] \[したがって \quad \lim _{u \rightarrow 0} g(u)=f'(x_0) \times 1=f'(x_0) \quad となって極限値は存在する。\] $\qquad すなわち、g(u)\ は積分可能となるから$
\[\lim _{n \rightarrow \infty}\{S_n(x_0)-f(x_0)\}=\lim _{n \rightarrow \infty}\cfrac{1}{\pi}\int _{-\pi}^{\pi}g(u)\sin (n+\dfrac{1}{2})u du \] $\quad は、$リーマン・ルベーグの定理$によりこの極限値は \ 0\ になる。$
$\quad ゆえに、f(x)\ が区分的になめらかならば、\quad n \longrightarrow \infty \quad とすると \quad S_n(x_0) \longrightarrow f(x_0) \quad となる。$
\[すなわち、f(x)\ が \ x=x_0 \ で連続ならば \qquad \cfrac{a_0}{2}+\sum_{k=1}^{\infty} (a_k\cos kx_0+b_k\sin kx_0)=f(x_0)\]
$(2)\ \ f(x)\ が \ x=x_0 \ で不連続な場合$
$\qquad g(x_0)=\cfrac{1}{2}\{f(x_0+0)+f(x_0-0)\} \quad とおくと \quad g(x_0)\ は、不連続点の値の平均値となります。$
\begin{eqnarray*} & &S_n(x_0)-g(x_0)\\ \\ &=&S_n(x_0)-\cfrac{f(x_0+0)+f(x_0-0)}{2}\\ \\ &=&\cfrac{1}{\pi}\int _{-\pi}^{\pi}f(u+x_0)\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du - 1 \times \cfrac{f(x_0+0)+f(x_0-0)}{2}\\ \\ &=&\cfrac{1}{\pi}\int _{-\pi}^{\pi}f(u+x_0)\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du - \cfrac{1}{\pi}\int _{-\pi}^{\pi}\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du \times \cfrac{f(x_0+0)+f(x_0-0)}{2}\\ \\ &=&\cfrac{1}{2\pi}\int _{-\pi}^{\pi}\big\{2f(u+x_0)-f(x_0+0)-f(x_0-0)\big\}\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du \\ \\ &=&\cfrac{1}{2\pi}\int _{-\pi}^{\pi}\big\{\big(f(u+x_0)-f(x_0+0)\big)+\big(f(u+x_0)-f(x_0-0)\big)\big\}\cfrac{\sin (n+\dfrac{1}{2})u}{2\sin \dfrac{u}{2}}du \\ \\ &=&\cfrac{1}{2\pi}\int _{-\pi}^{\pi}\cfrac{f(u+x_0)-f(x_0+0)}{2\sin \dfrac{u}{2}} \cdot \sin (n+\dfrac{1}{2})u du + \cfrac{1}{2\pi}\int _{-\pi}^{\pi}\cfrac{f(u+x_0)-f(x_0-0)}{2\sin \dfrac{u}{2}} \cdot \sin (n+\dfrac{1}{2})u du \\ \end{eqnarray*}
$\qquad h_1(u)=\cfrac{f(u+x_0)-f(x_0 + 0)}{2\sin \dfrac{u}{2}},\quad h_2(u)=\cfrac{f(u+x_0)-f(x_0 - 0)}{2\sin \dfrac{u}{2}} \quad はそれぞれ \quad u \longrightarrow +0 ,\quad u \longrightarrow -0 \quad とすると$
$\qquad 不定形であるが$
$\qquad h_1(u)=\cfrac{f(u+x_0)-f(x_0 + 0)}{u} \cdot \cfrac{\dfrac{u}{2}}{\sin \dfrac{u}{2}},\qquad h_2(u)=\cfrac{f(u+x_0)-f(x_0 - 0)}{u} \cdot \cfrac{\dfrac{u}{2}}{\sin \dfrac{u}{2}} \quad より$
$\qquad f(x)\ が区分的になめらかだから$
\[\quad \lim _{u \rightarrow +0} \cfrac{f(u+x_0)-f(x_0 + 0)}{u}=f'(x_0+0),\qquad \lim _{u \rightarrow -0} \cfrac{f(u+x_0)-f(x_0 - 0)}{u}=f'(x_0-0) \quad は存在する。\] \[したがって \lim _{u \rightarrow +0} h_1(u)=f'(x_0 + 0) \times 1=f'(x_0 + 0),\qquad \lim _{u \rightarrow -0} h_2(u)=f'(x_0 - 0) \times 1=f'(x_0 - 0) \] $\quad となって、極限値は存在する。\quad すなわち、h_1(u),\ \ h_2(u) \ は積分可能となるから$
\[\lim _{n \rightarrow \infty}\{S_n(x_0)-g(x_0)\}=\lim _{n \rightarrow \infty}\big\{ \cfrac{1}{2\pi}\int _{-\pi}^{\pi}h_1(u)\sin (n+\dfrac{1}{2})u du + \cfrac{1}{2\pi}\int _{-\pi}^{\pi}h_2(u)\sin (n+\dfrac{1}{2})u du \big\} \] $\quad は、リーマン・ルベーグの定理によりこの極限値は \ 0\ になる。$
$\quad したがって、f(x)\ が区分的になめらかならば、$
$\qquad n \longrightarrow \infty \quad とすると \quad S_n(x_0) \longrightarrow g(x_0)=\cfrac{f(x_0+0)+f(x_0-0)}{2} \quad となる$
\[すなわち、f(x)\ が \ x=x_0 \ で不連続ならば \quad \cfrac{a_0}{2}+\sum_{k=1}^{\infty} (a_k\cos kx_0+b_k\sin kx_0)= \cfrac{f(x_0+0)+f(x_0-0)}{2}\]
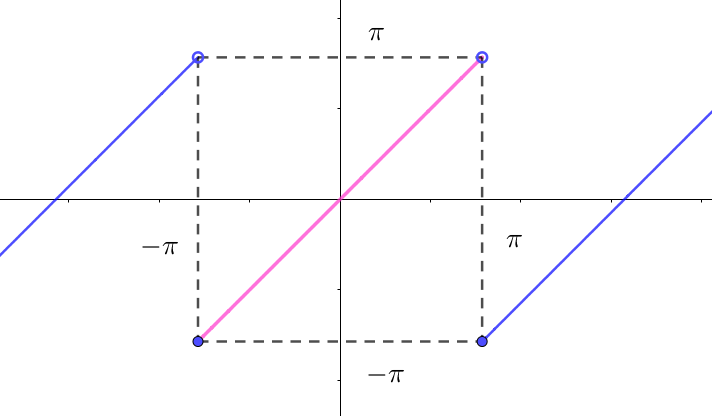
$例 \quad 右図の「ノコギリ波」\quad f(x)=x \quad (-\pi \leqq x < \pi)$
$\quad は周期 \ 2\pi \ の周期関数で$
$\quad f(\pi-0)=\pi,\quad f(\pi+0)=-\pi \quad だから \ x=\pi \ で不連続です。$
$\quad f(x)\ のフーリェ級数展開は($狭義のフーリェ級数$をご覧ください。)$
$\qquad f(x)=2\sin x -\sin 2x +\cfrac{2}{3}\sin 3x -\cfrac{2}{4}\sin 4x + \cdots $
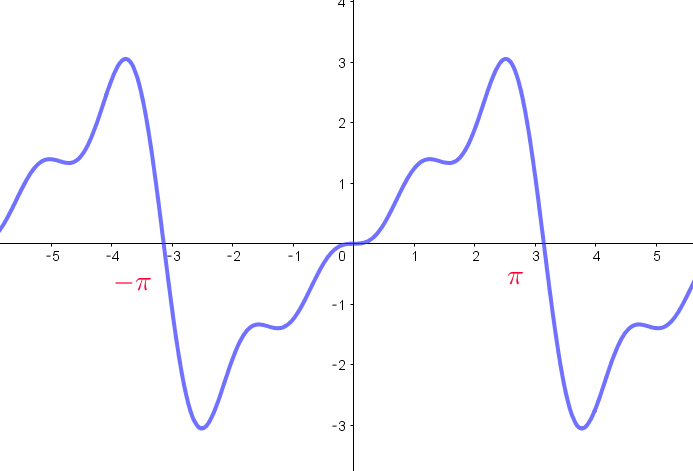
$右図は第 \ 4\ 項までの和のグラフですが、明らかに$
$\quad f(\pi)=\cfrac{1}{2}\big\{f(\pi-0)+f(\pi+0)\big\}=\cfrac{1}{2}(\pi-\pi)=0 \quad となっています。$
フーリェ級数メニュー に戻る
メインメニュー に戻る