早稲田大学(理系) 2023年　問題Ⅳ


$複素数平面上に \ 2\ 点 \ A(1),\ B(\sqrt{3}i)\ がある。ただし、i\ は虚数単位である。複素数 \ z\ に対し \ \ w=\cfrac{3}{z}\ \ で$
$表される点 \ w\ を考える。以下の問に答えよ。$
$(1)\ \ z=1,\ \ \cfrac{1+\sqrt{3}i}{2},\ \ \sqrt{3}i \ \ のときの \ w\ をそれぞれ計算せよ。$
$(2)\ \ 実数 \ t\ に対し \ \ z=(1-t)+t\sqrt{3}i \ \ とする。\alpha=\cfrac{3-\sqrt{3}i}{2}\ \ について、\alpha \ z\ \ の実部を求め、さらに$
$\quad (w-\alpha)(\overline{w-\alpha}) \ \ を求めよ。$
$(3)\ \ w\ と原点を結んでできる線分 \ L\ を考える。z\ が線分 \ AB\ 上を動くとき、線分 \ L\ が通過する範囲を$
$\quad 図示し、その面積を求めよ。$


(1)


$z=1\ \ のとき \quad w=\cfrac{3}{1}=3$

$z=\cfrac{1+\sqrt{3}i}{2} \ \ のとき \quad w=\cfrac{6}{1+\sqrt{3}i}=\cfrac{6(1-\sqrt{3}i)}{1+3}=\cfrac{3-3\sqrt{3}i}{2}$

$z=\sqrt{3}i \ \ のとき \quad w=\cfrac{3}{\sqrt{3}i}=\cfrac{\sqrt{3}i}{i^2}=-\sqrt{3}i$


(2)


$\alpha z \ の実部を \ \ Re(\alpha z)\ \ で表すことにすると$

$\quad Re(\alpha z)=Re \big(\cfrac{3-\sqrt{3}i}{2} \times \{(1-t)+t\sqrt{3}i\} \big)=\cfrac{3}{2} (1-t)+ \cfrac{\sqrt{3}}{2} \times \sqrt{3}t=\cfrac{3}{2}$

$また$
\begin{eqnarray*} & &(w-\alpha)(\overline{w-\alpha})\\ \\ &=&(\cfrac{3}{z}-\alpha)(\overline{\cfrac{3}{z}-\alpha})\\ \\ &=&\cfrac{3-\alpha z}{z} \times \big(\overline{\cfrac{3-\alpha z}{z}\big)}\\ \\ &=&\cfrac{3-\alpha z}{z} \times \cfrac{3-\overline{\alpha} \overline{z}}{\overline{z}}\\ \\ &=&\cfrac{(3-\alpha z)(3-\overline{\alpha} \overline{z})}{z \overline{z}}\\ \\ &=&\cfrac{9 +|\alpha |^2 |z|^2 -3(\alpha z + \overline{\alpha} \overline{z})}{|z|^2} \hspace{3em} (\ \ \cfrac{\alpha z + \overline{\alpha} \overline{z}}{2}=Re(\alpha z) \ \ だから\ \ )\\ \\ &=&\cfrac{9 +|\alpha |^2 |z|^2 -6Re(\alpha z )}{|z|^2} \\ \\ &=&\cfrac{9 +|\alpha |^2 |z|^2 -9}{|z|^2}\\ \\ &=&|\alpha |^2\\ \\ &=&(\cfrac{3}{2})^2+(\cfrac{\sqrt{3}}{2})^2\\ \\ &=&3 \end{eqnarray*}

(3)

　

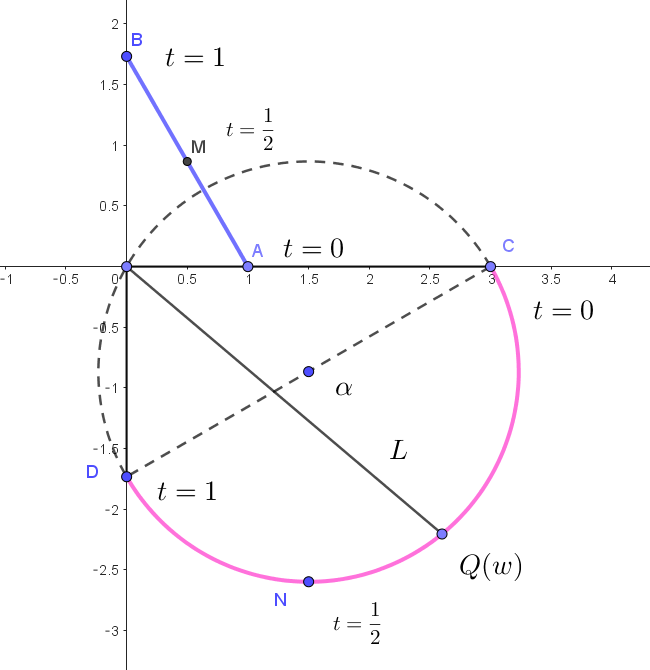
$線分 \ AB\ を \ \ t:(1-t)\ \ の比に内分する点を \ P(z)\ とすると \quad z=(1-t)+t\sqrt{3}i$

$(2)より　この \ z\ と \ \ \alpha=\cfrac{3-\sqrt{3}i}{2}\ \ に対して \quad |w-\alpha|=\sqrt{3}$

$よって \ \ 点 \ Q(w)\ は \ \ \alpha \ \ を中心、半径 \ \sqrt{3}\ \ の円周上にある。$

$(1)より$

$\quad A(1)\ \ は \ t=0\ のときで \ \ C(3)\ に写され、$

$\quad B(\sqrt{3}i)\ \ は \ t=1\ のときで \ \ D(-\sqrt{3}i)\ に写される。$

$\quad 線分 \ AB\ の中点 \ M(\cfrac{1+\sqrt{3}i}{2})\ \ は \ t=\cfrac{1}{2} \ のときで \ \ N(\cfrac{3-3\sqrt{3}i}{2})\ に写されるから$

$P(z)\ が線分 \ AB\ 上を動くとき、Q(w)\ は、上の円の下半分に写されることになる。$

　

$したがって、線分 \ L\ が通過する範囲は右図のとおりで、その面積 \ S\ は$

\begin{eqnarray*} S &=&\triangle OCD + 半円\\ \\ &=&\cfrac{1}{2} \times 3 \times \sqrt{3} + \cfrac{1}{2} \times \pi \times (\sqrt{3})^2\\ \\ &=&\cfrac{3(\sqrt{3}+\pi)}{2} \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る