早稲田大学(理系) 2021年 問題3
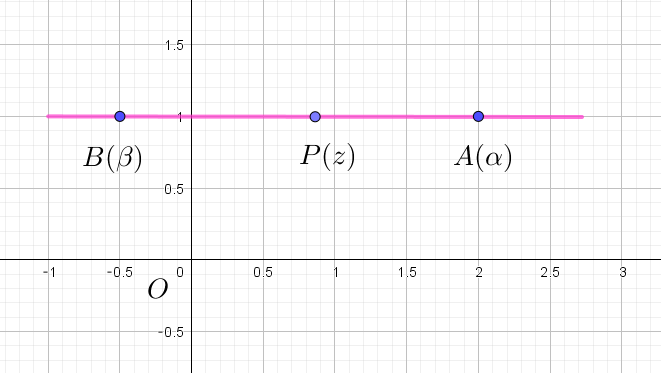
$複素数 \ \alpha =2+i,\ \beta=\cfrac{1}{2} + i\ \ に対応する複素数平面上の点を \ A(\alpha),\ B(\beta)\ とする。このとき、以下の$
$問に答えよ。$
$(1)\ \ 複素数平面上の点 \ C(\alpha ^2),\ D(\beta ^2)\ と原点 \ O\ の \ 3\ 点は一直線上にあることを示せ。$
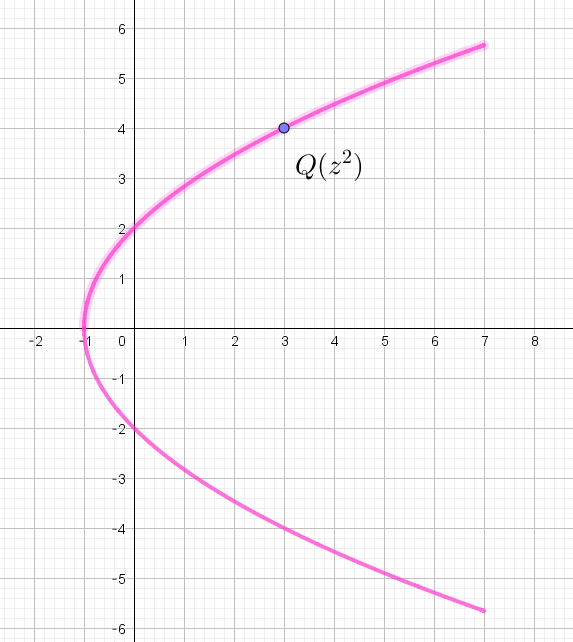
$(2)\ \ 点 \ P(z)\ が直線 \ AB\ 上を動くとき、z^2\ の実部を \ x,虚部を \ y\ として、点 \ Q(z^2)\ の軌跡を \ x,\ y\ の方程式$
$\qquad で表せ。$
$(3)\ \ 点 \ P(z)\ が、三角形 \ OAB\ の周および内部にあるとき、点 \ Q(z^2)\ 全体のなす図形を \ K\ とする。$
$\qquad K\ を複素数平面上に図示せよ。$
$(4)\ \ (3)の図形 \ K\ の面積を求めよ。$
$(解説)$
$(1)\ \ \alpha ^2 \ と \ \beta ^2\ \ を求めて関係を調べます。$
$(2)\ \ 直線 \ AB\ をパラメータを用いて表示し,z^2\ を計算します。 $
$(3)\ \ 三角形 \ OAB\ の \ 3\ 辺ごとに \ z^2\ を計算します。$
$(4)\ \ y\ 軸の分割で積分した方が簡単です。$
(1)
$\alpha ^2=(2+i)^2=3+4i,\qquad \beta ^2=(-\cfrac{1}{2}+i)^2=-\cfrac{3}{4}-i=-\cfrac{1}{4}(3+4i)$
$\beta ^2=-\cfrac{1}{4}\alpha ^2 \quad だから \quad 3\ 点 \ D,\ O,\ C\ はこの順に一直線上にある。$
(2)
$直線 \ AB \ は \ \ z=t+i\ \ (t\ は実数)\ とおけるから、z^2=t^2+2ti+i^2=t^2-1+2ti$
$\quad x=t^2-1, \quad y=2t$
$\quad t=\cfrac{y}{2} \quad を代入して \quad x=\big(\cfrac{y}{2}\big)^2-1 \qquad \therefore \ \ y^2=4(x+1)$
(3)
(i)$\ \ P(z)\ が辺 \ OA\ 上にあるとき$
$\qquad z=k\alpha \ \ (0 \leqq k \leqq 1) \quad だから \quad z^2=k^2\alpha ^2=k^2(3+4i)$
$\qquad x=3k^2, \quad y=4k^2 \quad より \quad y=\cfrac{4}{3}x \quad ただし \quad 0 \leqq k^2 \leqq 1 \quad より \quad 0 \leqq x \leqq 3$
(ii)$\ \ P(z)\ が辺 \ OB\ 上にあるとき$
$\qquad z=l\beta \ \ (0 \leqq l \leqq 1) \quad だから \quad z^2=l^2\beta^2=l^2(-\cfrac{3}{4}-i)$
$\qquad x=-\cfrac{3}{4}l^2, \quad y=-l^2 \quad より \quad y=\cfrac{4}{3}x \quad ただし \quad 0 \leqq l^2 \leqq 1 \quad より \quad -\cfrac{3}{4} \leqq x \leqq 0$
(iii)$\ \ P(z)\ が辺 \ AB\ 上にあるとき$
$\quad (2)より \quad x=t^2-1,\quad y=2t \quad だから \quad y^2=4(x+1) \quad ただし \quad -\cfrac{1}{2} \leqq t \leqq 2 \quad より \quad -1 \leqq y \leqq 4$
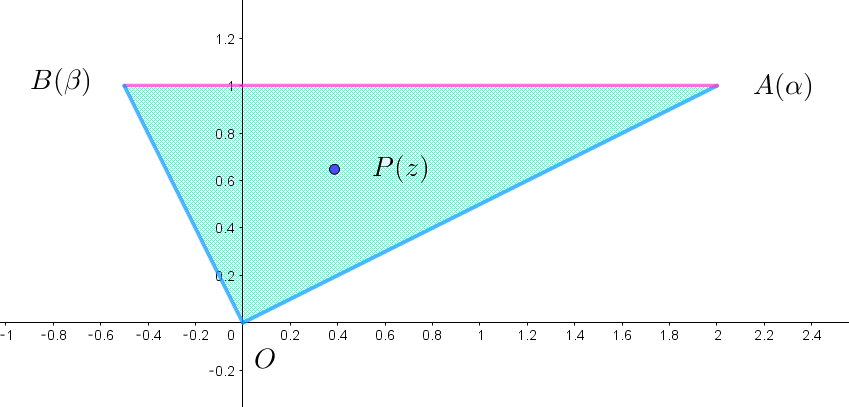
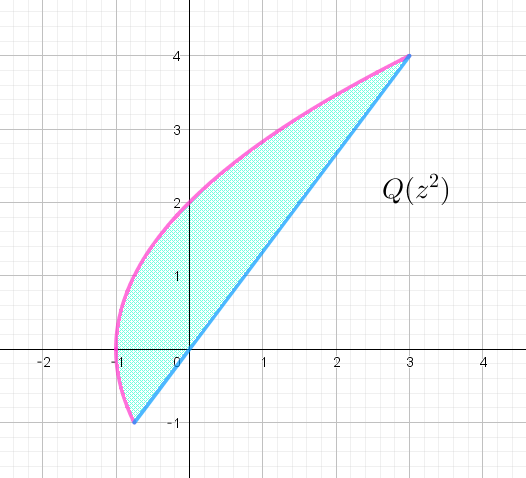
$\quad 図形 \ K\ は右図の周および内部である。$
(4)
$図形 \ k\ は、直線部分が \ \ x=\cfrac{3}{4}y,\quad 曲線部分が \ \ x=\cfrac{1}{4}y^2-1 \quad だからその面積 \ S\ は$
\begin{eqnarray*} S &=&\int _{-1}^4\{\cfrac{3}{4}y -(\cfrac{1}{4}y^2-1)\}dy\\ \\ &=&\big[\cfrac{3}{8}y^2-\cfrac{1}{12}y^3+y\big]_{-1}^4\\ \\ &=&\cfrac{3}{8} \times 16-\cfrac{1}{12} \times 64 +4 -(\cfrac{3}{8}+\cfrac{1}{12}-1)\\ \\ &=&\cfrac{125}{12} \end{eqnarray*}
メインメニュー に戻る