早稲田大学(理系) 2021年 問題2
$整式 \ f(x)=x^4-x^2+1\ \ について、以下の問に答えよ。$
$(1)\ \ x^6 \ を \ f(x)\ で割ったときの余りを求めよ。$
$(2)\ x^{2021}\ を \ f(x)\ で割ったときの余りを求めよ。$
$(3)\ 自然数 \ n\ が \ 3\ の倍数であるとき、(x^2-1)^n -1\ \ が \ f(x)\ で割り切れることを示せ。$
$(解説)$
$(1)\ \ ごく普通に筆算の割り算をおこないます。$
$(2)\ \ (1)の結果をつかうために \ 2021\ を \ 6\ で割って商と余りを求めます。 $
$(3)\ \ (x^2-1)^3-1 \ \ を展開した式がポイントです。$
(1)
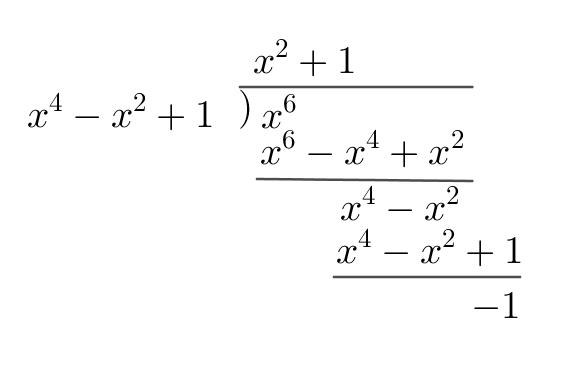
$\quad 右のとおり割り算をおこなって、余りは \quad -1$
(2)
$(1)より \quad x^6=(x^2+1)f(x)-1 \ \ で \quad 2021=6 \times 336+5 \quad だから$
\begin{eqnarray*} x^{2021} &=&x^{6 \times 336+5}\\ \\ &=&(x^6)^{336} \times x^5\\ \\ &=&((x^2+1)f(x)-1)^{336} \times x^5\\ \\ &=&\big(\sum_{k=0}^{336}{}_{336}C_k (x^2+1)^kf(x)^k (-1)^{336-k}\big) \times x^5\\ \\ &=&\big(\sum_{k=1}^{336}{}_{336}C_k (x^2+1)^kf(x)^k (-1)^{336-k}+(-1)^{336}\big) \times x^5\\ \\ &=&x^5 \big(\sum_{k=1}^{336}{}_{336}C_k (x^2+1)^kf(x)^k (-1)^{336-k}\big)+ x^5\\ \\ &=&f(x)\Big\{x^5 \big(\sum_{k=1}^{336}{}_{336}C_k (x^2+1)^kf(x)^{k-1} (-1)^{336-k}\big)\Big\}+ x^5\\ \end{eqnarray*}
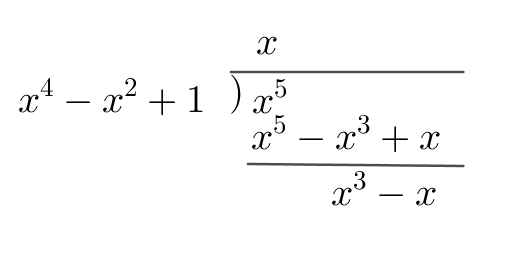
$第 \ 1\ 項目は、f(x)\ を因数に含むので、x^{2021}\ を \ f(x)\ で割った余りは、$
$x^5\ \ を \ f(x)\ で割った余りに等しい。$
$右の計算より、余りは \quad x^3-x$
(3)
$\quad (1)より \quad x^6=(x^2+1)f(x)-1 \quad だから$
\begin{eqnarray*} & &(x^2-1)^3-1\\ \\ &=&x^6-3x^4+3x^2-2\\ \\ &=&\big((x^2+1)f(x)-1\big)-3x^4+3x^2-2\\ \\ &=&(x^2+1)f(x)-3(x^4-x^2+1)\\ \\ &=&(x^2+1)f(x)-3f(x)\\ \\ &=&(x^2-2)f(x) \end{eqnarray*}
$\therefore \ \ (x^2-1)^3=(x^2-2)f(x)+1$
$\quad n=3k \ \ (kは自然数)とおくと$
\begin{eqnarray*} & &(x^2-1)^n -1\\ \\ &=&(x^2-1)^{3k} -1\\ \\ &=&\big((x^2-2)f(x)+1\big)^k-1\\ \\ &=&\sum_{l=0}^k{}_kC_l (x^2-2)^lf(x)^l-1\\ \\ &=&\sum_{l=1}^k{}_kC_l (x^2-2)^lf(x)^l+1-1\\ \\ &=&\sum_{l=1}^k{}_kC_l (x^2-2)^lf(x)^l\\ \\ &=&f(x)\sum_{l=1}^k{}_kC_l (x^2-2)^lf(x)^{l-1}\\ \end{eqnarray*} $よって \quad n\ が \ 3\ の倍数のとき、(x^2-1)^n -1 は\ f(x)\ で割り切れる。$
$(別解)$
$(x^2-1)^{3k} -1 \ \ が \ f(x)\ で割り切れることを数学的帰納法で証明する。$
$(x^2-1)^{3k} -1 =(x^6-3x^4+3x^2-1)^k-1 \quad だから$
(i)$\ \ k=1 \quad のとき$
$\quad 上の証明の \quad (x^2-1)^3-1=(x^2-2)f(x) \quad より、f(x)\ で割り切れるから \ k=1 \ \ のとき成りたつ$
(ii)$\ \ k=m \quad のとき成りたつとすると$
$\quad (x^6-3x^4+3x^2-1)^m-1=f(x)g(x) \quad (g(x)\ は整式)\ \ とおける$
$\quad このとき$
\begin{eqnarray*} & &(x^6-3x^4+3x^2-1)^{m+1}-1\\ \\ &=&(x^6-3x^4+3x^2-1)(x^6-3x^4+3x^2-1)^m-1\\ \\ &=&\big((x^2-2)f(x)+1\big)\big(f(x)g(x)+1\big)-1\\ \\ &=&\big((x^2-2)f(x)+1\big)f(x)g(x)+ \big(x^2-2)f(x)+1-1\\ \\ &=&\big((x^2-2)f(x)+1\big)f(x)g(x)+ \big(x^2-2)f(x)\\ \\ &=&\Big(\big((x^2-2)f(x)+1\big)g(x)+ x^2-2\Big)f(x)\\ \end{eqnarray*}
$\quad これは、f(x)\ で割り切れるから \ k=m+1 \ \ のときも成りたつ。$
(i),(ii)$\ \ よりすべての自然数 \ k\ について成りたつから、自然数 \ n\ が \ 3\ の倍数であるとき、$
$(x^2-1)^n -1\ \ は \ f(x)\ で割り切れる。$
メインメニュー に戻る