早稲田大学(理系) 2021年 問題1
$xy\ 平面上の曲線 \ y=x^3 \ を \ C\ とする。C\ 上の \ 2\ 点 \ A(-1,\ -1),\ B(1,\ 1)\ をとる。さらに、C\ 上で原点 \ O\ と$
$B\ の間に動点 \ P(t,\ t^3)\ \ (0 < t < 1)\ をとる。このとき、以下の問に答えよ。$
$(1)\ \ 直線 \ AP\ と \ x\ 軸のなす角を \ \alpha \ とし、直線 \ PB\ と \ x\ 軸のなす角を \ \beta \ とするとき、\tan \alpha,\ \ \tan \beta \ を \ t\ を$
$\qquad 用いて表せ。ただし、0 < \alpha < \cfrac{\pi}{2},\ \ 0 < \beta < \cfrac{\pi}{2}\ \ とする。$
$(2)\ \ \tan \angle APB \ \ を \ t\ を用いて表せ。$
$(3)\ \ \angle APB \ \ を最小にする \ t\ の値を求めよ。$
$(解説)$
$(1)\ \ 直線が \ x\ 軸の正方向となす角を \theta \ とすると 傾き \ m=\tan \theta \ \ です。$
$(2)\ \ 三角形の \ 2\ つの内角の和は、残りの角の外角に等しくなります。$
$(3)\ \ 分数関数となるので、微分法で求めます。$
(1)
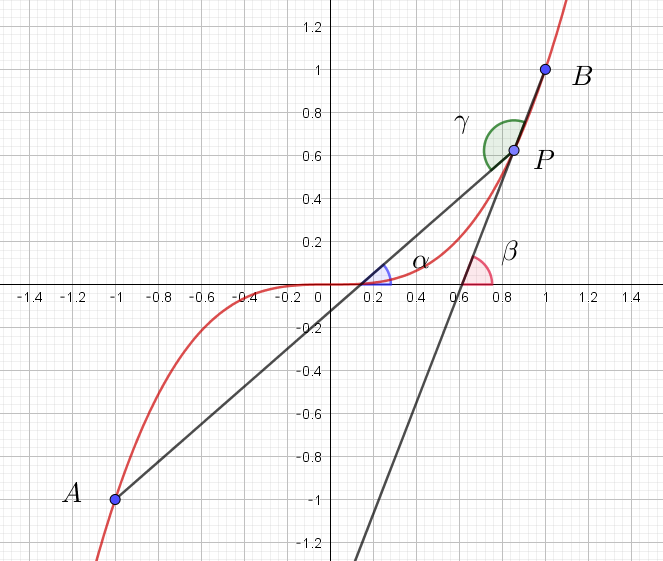
$\tan \alpha=直線APの傾き=\cfrac{t^3+1}{t+1}=t^2-t+1$
$\tan \beta =直線PBの傾き=\cfrac{1-t^3}{1-t}=1+t+t^2$
(2)
$\angle APB=\gamma \ \ とおくと$
$\quad \alpha +(\pi -\gamma)=\beta \quad より \quad \gamma =\pi - \beta + \alpha $
\begin{eqnarray*} \tan \angle APB &=&\tan \gamma \\ \\ &=&\tan(\pi - (\beta - \alpha) )\\ \\ &=&-\tan(\beta -\alpha )\\ \\ &=&-\cfrac{\tan \beta -\tan \alpha}{1+ \tan \beta \tan \alpha}\\ \\ &=&-\cfrac{(t^2+t+1)-(t^2-t+1)}{1+ (t^2+t+1)(t^2-t+1)}\\ \\ &=&-\cfrac{2t}{1+ (t^2+1)^2-t^2}\\ \\ &=&-\cfrac{2t}{t^4+ t^2+2}\\ \end{eqnarray*}
(3)
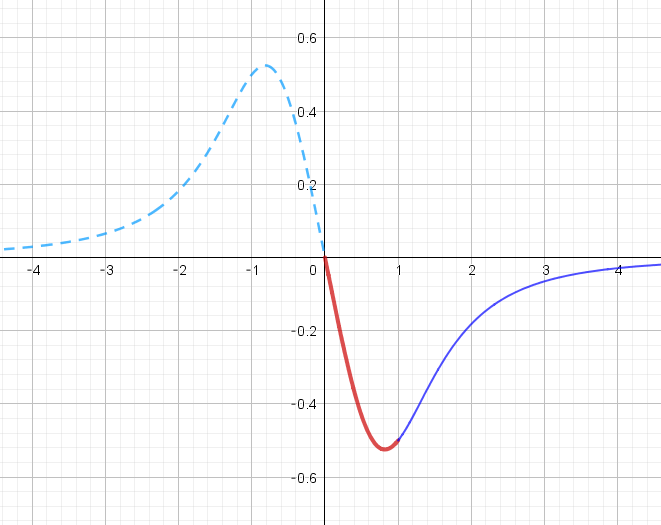
$\quad f(t)=-\cfrac{2t}{t^4+ t^2+2}\ \ (0 < t < 1) \ \ とおくと$
\begin{eqnarray*} f'(t) &=&-\cfrac{2(t^4+t^2+2)-2t(4t^3+2t)}{(t^4+ t^2+2)^2}\\ \\ &=&\cfrac{2(3t^4+t^2-2)}{(t^4+ t^2+2)^2}\\ \\ &=&\cfrac{2(t^2+1)(3t^2-2)}{(t^4+ t^2+2)^2}\\ \end{eqnarray*}
$\quad f'(t)=0 \quad より \quad t=\sqrt{\cfrac{2}{3}}=\cfrac{\sqrt{6}}{3}$
\[
\begin{array}{c||c|c|c|c|c}
\hline
t & 0 & \cdots & \cfrac{\sqrt{6}}{3} & \cdots & 1\\
\hline
f'(x) & & - & 0 & + & \\
\hline
f(x) & & \searrow & 極小 & \nearrow & \\
\end{array}
\]
$f(t)\ は \ \ t =\cfrac{\sqrt{6}}{3} \ \ で極小かつ最小となる。$
$最小値は \quad f(\cfrac{\sqrt{6}}{3})=\cfrac{-\dfrac{2\sqrt{6}}{3}}{\dfrac{4}{9}+\dfrac{2}{3}+2}=-\cfrac{3\sqrt{6}}{14}$
$なお、グラフは右のとおりです。$
$(補充)$
$最小値をとるときの \ \angle APB=\gamma \ \ を関数電卓で計算すると$
$\quad \tan \gamma =-\cfrac{3\sqrt{6}}{14}=-0.525 \quad だから \quad \gamma =180°- 27.7°=152.3°\ \ です。$
$また$
$\quad \tan \alpha=\cfrac{2}{3}-\cfrac{\sqrt{6}}{3}+1=\cfrac{5-\sqrt{6}}{3}=0.850 \quad より \quad \alpha =40.4°$
$\quad \tan \beta=\cfrac{2}{3}+\cfrac{\sqrt{6}}{3}+1=\cfrac{5+\sqrt{6}}{3}=2.483 \quad より \quad \beta =68.1°$
メインメニュー に戻る