宇都宮大学(理系) 2025年 問題3
$e\ を自然対数の底とする。x \geqq 0 \ \ で定義された関数 \ \ f(x)=e^{-x} |\sin x| \ \ を考え、曲線 \ y=f(x)\ と \ x\ 軸との$
$共有点の \ x\ 座標を、小さい順に \ t_0,\ t_1,\ t_2,\ \cdots \ \ とする。ただし、t_0=0 \ \ である。n=1,\ 2,\ 3,\ \cdotsに対して、$
$t_{n-1} \leqq x_n \leqq t_n \ \ において、曲線 \ y=f(x) \ と \ x\ 軸で囲まれた部分の面積を \ S_n \ とする。このとき、次の問いに$
$答えよ。$
$(1)\ \ f(\dfrac{\pi}{2}),\ \ f(\pi),\ \ f(\dfrac{3\pi}{2})\ \ を求めよ。$
\[(2)\ \ 極限値 \ \ \lim_{h \rightarrow +0} \dfrac {f(\pi + h)-f(\pi)}{h}\ \ および \ \ \lim_{h \rightarrow -0} \dfrac {f(\pi + h)-f(\pi)}{h}\ \ を求めよ。また、関数 \ f(x)\ が \ x=\pi \ で\]
$\quad 微分可能かどうかを判定せよ。$
$(3)\ \ g(x)=e^{-x}(a\sin x+b\cos x) \ \ とするとき、g'(x)=e^{-x}\sin x \ \ が成り立つように定数 \ a,\ b\ の値を定めよ。$
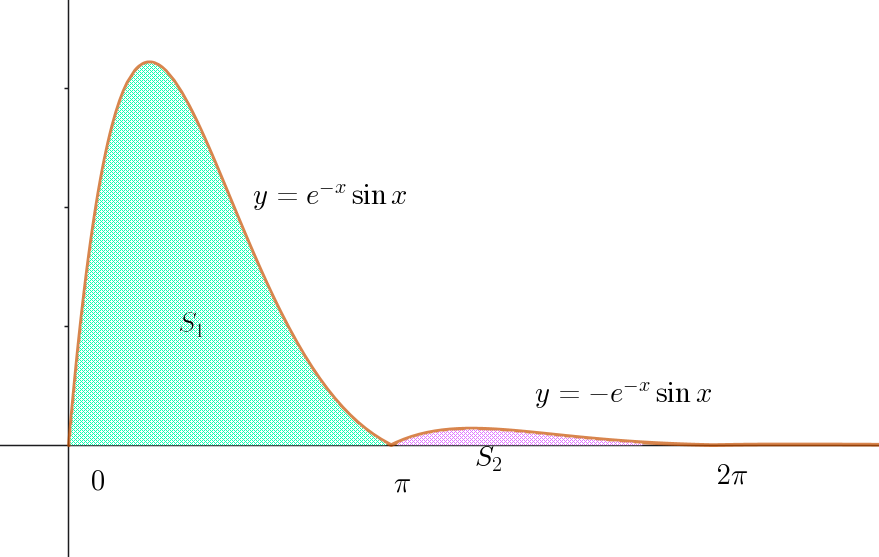
$(4)\ \ S_1 を求めよ。$
\[(5)\ \ \sum_{n=1}^{\infty} S_n \ \ を求めよ。\]
(1)
$f(\dfrac{\pi}{2})=e^{-\scriptsize{\dfrac{\pi}{2}}}|\sin \dfrac{\pi}{2}|=e^{-\scriptsize{\dfrac{\pi}{2}}}$
$f(\pi)=e^{-\pi}|\sin \pi|=0$
$f(\dfrac{3\pi}{2})=e^{-\scriptsize{\dfrac{3\pi}{2}}}|\sin \dfrac{3\pi}{2}|=e^{-\scriptsize{\dfrac{3\pi}{2}}}$
(2)
(i)$\ \ h > 0 \ \ のとき \quad \pi < \pi + h \quad だから \quad f(x)=-e^{-x}\sin x$
\begin{eqnarray*} & &\lim_{h \rightarrow +0} \dfrac {f(\pi + h)-f(\pi)}{h}\\ \\ &=&\lim_{h \rightarrow +0} \dfrac {-e^{-(\pi + h)}\sin (\pi + h)}{h}\\ \\ &=&\lim_{h \rightarrow +0} \dfrac {e^{-(\pi + h)}\sin h}{h}\\ \\ &=&e^{-\pi} \end{eqnarray*}
(ii)$\ \ h < 0 \ \ のとき \quad \pi + h < \pi \quad だから \quad f(x)=e^{-x}\sin x$
\begin{eqnarray*} & &\lim_{h \rightarrow -0} \dfrac {f(\pi + h)-f(\pi)}{h}\\ \\ &=&\lim_{h \rightarrow -0} \dfrac {e^{-(\pi + h)}\sin (\pi + h)}{h}\\ \\ &=&\lim_{h \rightarrow -0} \dfrac {-e^{-(\pi + h)}\sin h}{h}\\ \\ &=&-e^{-\pi} \end{eqnarray*}
$右方微分係数と左方微分係数が一致しないので、f(x)\ は \ x=\pi \ で微分可能でない。$
(3)
$g(x)=e^{-x}(a\sin x+b\cos x) \ \ のとき$
$g'(x)=-e^{-x}(a\sin x+b\cos x)+e^{-x}(a\cos x-b\sin x)=e^{-x}\big((-a-b)\sin x+(a-b)\cos x\big)$
$g'(x)=e^{-x}\sin x \ \ が成り立つとき$
\[ \hspace{1em} \left\{ \begin{array}{l} -a-b=1\\ a-b=0\\ \end{array} \right. \]
$これを解いて \quad a=b=-\dfrac{1}{2}$
$すなわち \quad g(x)=-\dfrac{1}{2}e^{-x}(\sin x+\cos x) \ \ のとき \quad g'(x)=e^{-x}\sin x$
$(補充)$
\[このことは \quad \int e^{-x}\sin x=-\dfrac{1}{2}e^{-x}(\sin x+\cos x) \quad であることを示しています。\]
$なお、この公式は通常次のように、部分積分を \ 2\ 回つかって求めます。$
\begin{eqnarray*} I &=&\int e^{-x}\sin x dx\\ \\ &=&-e^{-x}\sin x + \int e^{-x}\cos x dx\\ \\ &=&-e^{-x}\sin x -e^{-x}\cos x -\int e^{-x}\sin x dx\\ \\ &=&-e^{-x}(\sin x + \cos x ) -I\\ \end{eqnarray*} $よって \quad I=-\dfrac{1}{2}e^{-x}(\sin x+\cos x)$
(4)
\begin{eqnarray*} S_1 &=&\int_0^{\pi} e^{-x}\sin xdx\\ \\ &=&\big[-\dfrac{1}{2}e^{-x}(\sin x+\cos x)\big]_0^{\pi}\\ \\ &=&-\dfrac{1}{2}(e^{-\pi}\cos \pi - e^0 \cos 0)\\ \\ &=&\dfrac{1}{2}(e^{-\pi} +1) \end{eqnarray*}
(5)
\[S_n=\int_{(n-1)\pi}^{n\pi} e^{-x}|\sin x|dx \]
(i)$\ \ n \ が奇数のとき、 区間 \ [(n-1)\pi,\ n\pi]\ \ で \quad |\sin x|=\sin x \quad だから$
\begin{eqnarray*} S_n &=&\int_{(n-1)\pi}^{n\pi} e^{-x}\sin xdx\\ \\ &=&\big[-\dfrac{1}{2}e^{-x}(\sin x+\cos x)\big]_{(n-1)\pi}^{n\pi}\\ \\ &=&-\dfrac{1}{2}\big\{(e^{-n\pi}(\sin n\pi + \cos n\pi) - e^{-(n-1)\pi}(\sin (n-1)\pi +\cos (n-1)\pi)\big\}\\ \\ &=&-\dfrac{1}{2}\big\{(e^{-n\pi} \times (-1) - e^{-(n-1)\pi} \times 1\big\}\\ \\ &=&\dfrac{1}{2}\big(e^{-n\pi} + e^{-(n-1)\pi}\big )\\ \end{eqnarray*}
(ii)$\ \ n \ が偶数のとき、 区間 \ [(n-1)\pi,\ n\pi]\ \ で \quad |\sin x|=-\sin x \quad だから$
\begin{eqnarray*} S_n &=&\int_{(n-1)\pi}^{n\pi} e^{-x}(-\sin x)dx\\ \\ &=&\big[\dfrac{1}{2}e^{-x}(\sin x+\cos x)\big]_{(n-1)\pi}^{n\pi}\\ \\ &=&\dfrac{1}{2}\big\{(e^{-n\pi}(\sin n\pi + \cos n\pi) - e^{-(n-1)\pi}(\sin (n-1)\pi +\cos (n-1)\pi)\big\}\\ \\ &=&\dfrac{1}{2}\big\{(e^{-n\pi} \times 1 - e^{-(n-1)\pi} \times (-1)\big\}\\ \\ &=&\dfrac{1}{2}\big(e^{-n\pi} + e^{-(n-1)\pi}\big )\\ \end{eqnarray*}
$よって \quad n\ が奇数、偶数にかかわらず$
$S_n=\dfrac{1}{2}\big(e^{-n\pi} + e^{-(n-1)\pi}\big )=\dfrac{1}{2}(e^{\pi}+1)e^{-n\pi}=\dfrac{1}{2}(e^{\pi}+1)\big(e^{-\pi}\big)^n$
$S_n \ は \ 初項 \ S_1,\ \ 公比 \ e^{-\pi}\ \ の等比数列で、 0< e^{-\pi}< 1 \ \ だから無限等比級数は収束して$
\begin{eqnarray*} & &\sum_{n=1}^{\infty} S_n \\ \\ &=&\sum_{n=1}^{\infty} \dfrac{1}{2}(e^{\pi}+1)\big(e^{-\pi}\big)^n\\ \\ &=&\dfrac{1}{2}(e^{\pi}+1) \times \dfrac{e^{-\pi}}{1-e^{-\pi}}\\ \\ &=&\dfrac{1}{2}(e^{\pi}+1) \times \dfrac{1}{e^{\pi}-1}\\ \\ &=&\dfrac{e^{\pi}+1}{2(e^{\pi}-1)}\\ \end{eqnarray*}
メインメニュー に戻る