宇都宮大学(理系) 2025年 問題2
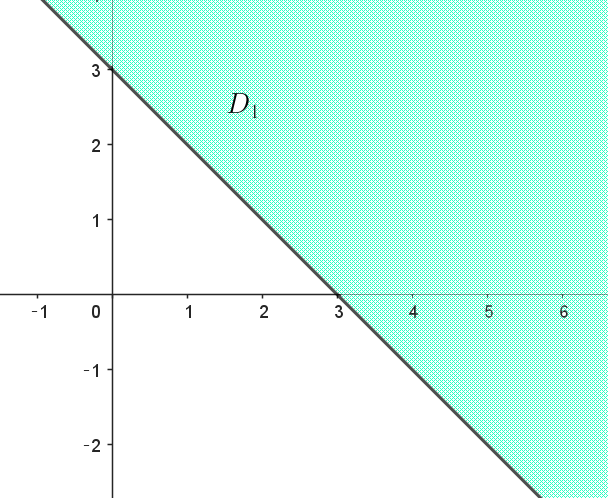
$複素数平面上で \ \ |z-3-3i| \leqq |z|\ \ を満たす点 \ z\ が存在する領域を \ D_1\ とする。また、z\ が \ D_1\ を動くとき、$
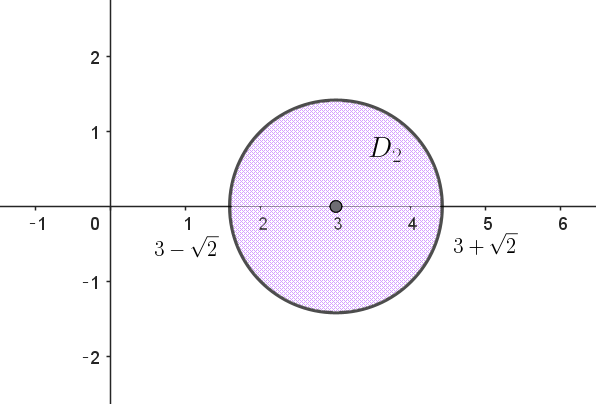
$w=2+i+\dfrac{6}{z}\ \ で表される点 \ w\ が存在する領域を \ D_2\ とし、D_1\ と \ D_2\ の共通部分を \ D\ とする。次の問い$
$に答えよ。$
$(1)\ \ z_1=\dfrac{\sqrt{6}}{4} - \dfrac{3\sqrt{2}}{4}i \ \ と定めるとき、z_1\ を極形式で表せ。ただし、偏角 \ \theta \ は \ \ 0 \leqq \theta < 2\pi \ \ とする。$
$(2)\ \ 複素数平面上に \ D_1\ を図示せよ。$
$(3)\ \ 複素数平面上に \ D_2\ を図示せよ。$
$(4)\ \ 点A(\alpha)\ が \ D\ を動くとき、\tan(\arg \alpha)\ のとりうる値の範囲を求めよ。ただし、\arg \alpha \ は \ \alpha \ の偏角を表す。$
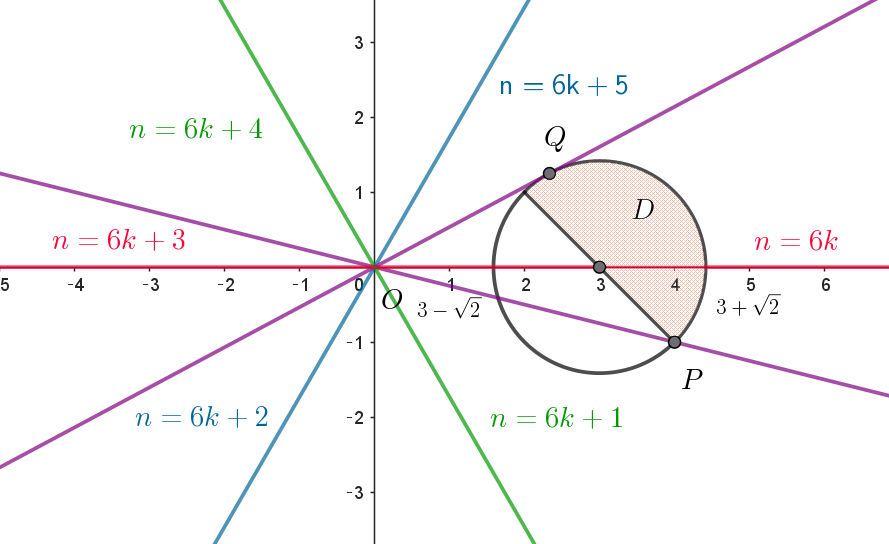
$(5)\ \ n\ を自然数とする。(1)の \ z_1 \ に対し、点(z_1)^n \ \ が \ D\ に含まれるような最小の \ n\ の値を求めよ。$
(1)
$z_1=\dfrac{\sqrt{6}}{4} - \dfrac{3\sqrt{2}}{4}i=\dfrac{\sqrt{6}}{4}(1-\sqrt{3}i)\quad より$
$|z_1|=\dfrac{\sqrt{6}}{4} \times \sqrt{1^2+(-\sqrt{3})^2}=\dfrac{\sqrt{6}}{4} \times 2=\dfrac{\sqrt{6}}{2}$
$\arg z_1=2\pi - \dfrac{\pi}{3}=\dfrac{5}{3}\pi$
$よって \quad z_1=\dfrac{\sqrt{6}}{2}\big(\cos \dfrac{5}{3}\pi +i\sin \dfrac{5}{3}\pi\big)$
(2)
$|x-3+(y-3)i| \leqq |x+yi|$
$(x-3)^2+(y-3)^2 \leqq x^2+y^2$
$-6x-6y+18 \leqq 0$
$x+y \geqq 3$
$領域 \ D_1 \ は右図のとおり$
(3)
$w=2+i+\dfrac{6}{z}\ \ より \quad w-2-i=\dfrac{6}{z} \qquad z=\dfrac{6}{w-2-i}$
$これを \ \ |z-3-3i| \leqq |z| \ \ に代入して$
$|\dfrac{6}{w-2-i}-3-3i| \leqq |\dfrac{6}{w-2-i}| $
$|\dfrac{6-(3+3i)(w-2-i)}{w-2-i}| \leqq |\dfrac{6}{w-2-i}|$
$|2-(1+i)(w-2-i)| \leqq 2$
$|3+3i-(1+i)w| \leqq 2$
$|3(1+i)-(1+i)w| \leqq 2$
$|(1+i)(3-w)| \leqq 2$
$\sqrt{2}|w-3| \leqq 2$
$|w-3| \leqq \sqrt{2}$
$よって \ \ w\ は \ C(3)\ を中心に、半径 \ \sqrt{2}\ の円の周および内部で、領域 \ D_2\ は上図のとおり$
(4)
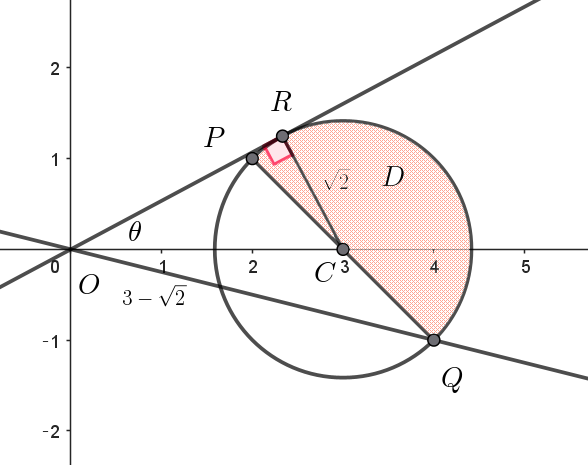
$直線 \ \ x+y=3 \ \ と円 \ \ (x-3)^2+y^2=2 \ \ の交点は$
$x-3=-y \ \ を代入して \quad (-y)^2+y^2=2$
$2y^2=2 \qquad y^2=1 \ \ より \quad y=\pm 1$
$y=1 \ \ のとき \ \ x=2,\quad y=-1 \ \ のとき \ \ x=4$
$P(z_1)=2+i,\quad Q(z_2)=4-i$
$\tan(\arg(z_1))=\dfrac{1}{2},\quad \tan(\arg(z_2))=-\dfrac{1}{4}$
$直線OR\ を円の接線とすると \quad OR \perp CR$
$直角三角形 OCR \ \ において \quad OC=3,\ \ CR=\sqrt{2}\ \ だから \quad OR=\sqrt{7}$
$R(z_3)\ とおくと \quad \tan (\arg z_3)=\dfrac{RC}{OR}=\dfrac{\sqrt{2}}{\sqrt{7}}=\dfrac{\sqrt{14}}{7}$
$\dfrac{1}{2} < \dfrac{\sqrt{2}}{\sqrt{7}} \quad だから \quad \tan(\arg z_1) < \tan(\arg z_3)$
$\tan(\arg z_2) \leqq \tan(\arg \alpha) \leqq \tan(\arg z_3) \quad より \quad -\dfrac{1}{4} \leqq \tan(\arg \alpha) \leqq \dfrac{\sqrt{14}}{7}$
(5)
$(1)より \quad z_1=\dfrac{\sqrt{6}}{2}\big(\cos \dfrac{5}{3}\pi +i\sin \dfrac{5}{3}\pi\big) \quad だから$
$(z_1)^n=\big(\dfrac{\sqrt{6}}{2}\big)^n\big(\cos \dfrac{5n}{3}\pi +i\sin \dfrac{5n}{3}\pi\big)$
$k\ を整数として$
(i)$\ \ n=6k \ \ のとき \quad \arg\big((z_1)^{6k}\big)=\dfrac{5 \times 6k}{3}\pi =0$
(ii)$\ \ n=6k+1 \ \ のとき \quad \arg\big((z_1)^{6k+1}\big)=\dfrac{5(6k+1)}{3}\pi =\dfrac{5}{3}\pi \qquad \tan \dfrac{5}{3}\pi=-\sqrt{3}$
(iii)$\ \ n=6k+2 \ \ のとき \quad \arg\big((z_1)^{6k+2}\big)=\dfrac{5(6k+2)}{3}\pi=\dfrac{4}{3}\pi \qquad \tan \dfrac{4}{3}\pi =\sqrt{3}$
(iv)$\ \ n=6k+3 \ \ のとき \quad \arg\big((z_1)^{6k+3}\big)=\dfrac{5(6k+3)}{3}\pi=\pi \qquad \tan \pi=0 \ \ であるが実軸負の方向$
(v)$\ \ n=6k+4 \ \ のとき \quad \arg\big((z_1)^{6k+4}\big)=\dfrac{5(6k+4)}{3}\pi=\dfrac{2}{3}\pi \qquad \tan \dfrac{2}{3}\pi=-\sqrt{3}$
(vi)$\ \ n=6k+5 \ \ のとき \quad \arg\big((z_1)^{6k+5}\big)=\dfrac{5(6k+5)}{3}\pi=\dfrac{1}{3}\pi \qquad \tan \dfrac{1}{3}\pi=\sqrt{3}$
$以上、 n=6k+1,6k+2,6k+3,6k+4,6k+5 について 点((z_1)^n はDに含まれない。$
$次に、n=6\ \ (k=1)\ \ について絶対値を調べる、$
$|z_1|^6=\big(\dfrac{\sqrt{6}}{2}\big)^6=\dfrac{27}{8}$
$3 < \dfrac{27}{8} < 3+\sqrt{2} \quad だから \ \ 点(z_1)^6 \ \ は \ D\ に含まれる。$
$したがって、点(z_1)^n \ \ が \ D\ に含まれるような最小の \ n\ は \quad n=6$
$(補充)$
$\ \ n=12\ \ (k=2)\ \ のとき$
$|z_1|^{12}=\big(\dfrac{\sqrt{6}}{2}\big)^{12}=\big(\dfrac{27}{8}\big)^2=10.8 $
$ 3+\sqrt{2}=4.4 \ \ だから \ \ 点(z_1)^{12}\ \ は \ D\ に含まれない。$
$\dfrac{27}{8} < \big(\dfrac{27}{8}\big)^2 <\big(\dfrac{27}{8}\big)^3 <\cdots \quad だから$
$点(z_1)^n \ \ (n=6k,\ k=2,\ 3,\ \cdots)\ \ は \ D\ に含まれない。$
$よって D\ に含まれるのは \ \ n=6\ \ ただ \ 1\ つだけである。$
メインメニュー に戻る