筑波大学(理系) 2025年 問題6
\[f(x)=\sqrt{x}e^{-\frac{x^2}{4}} \ \ (x \geqq 0) \ \ とし、\alpha =\int_0^5f(x)dx \ \ とする。\]
$(1)\ \ f(x)\ \ (x \geqq 0) \ \ が最大値をとることを示し、その値 \ M\ を求めよ。$
$(2)\ \ 0 \leqq x \leqq 5 \ \ において \ \ e^{-\frac{25}{4}}\sqrt{x} \leqq f(x) \ \ を示せ。また、\dfrac{10}{3}f(5) \leqq \alpha \ \ を示せ。$
$(3)\ \ Mは(1)で求めたものとし、実数 \ t\ は \ \ \dfrac{2}{3} f(5) \leqq t \leqq M \ \ の範囲を動くとする。曲線 \ \ y=f(x)-t \ \ (x \geqq 0) $
$\quad 2\ 直線 \ \ x=0,\ \ x=5 ,\ \ および \ x\ 軸で囲まれた図形を、x\ 軸の周りに \ 1\ 回転させてできる回転体の体積を$
$\quad V(t)\ とする。V(t)\ の最小値を \ \alpha \ を用いて表せ。$
(1)
$f(x)=\sqrt{x}e^{-\frac{x^2}{4}}=x^{\frac{1}{2}}e^{-\frac{x^2}{4}} \ \ より$
\begin{eqnarray*} f'(x) &=&\dfrac{1}{2}x^{-\frac{1}{2}}e^{-\frac{x^2}{4}}+x^{\frac{1}{2}} \times (-\dfrac{x}{2})e^{-\frac{x^2}{4}}\\ \\ &=&\dfrac{1}{2}(x^{-\frac{1}{2}}- x^{\frac{3}{2}})e^{-\frac{x^2}{4}}\\ \\ &=&\dfrac{1}{2}\big(\dfrac{1}{\sqrt{x}} - x\sqrt{x}\big)e^{-\frac{x^2}{4}}\\ \\ &=&\dfrac{1}{2\sqrt{x}}(1- x^2)e^{-\frac{x^2}{4}}\\ \end{eqnarray*}
$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & 1 & \cdots \\ \hline f'(x)'& & + & 0 & - \\ \hline f(x)& & \nearrow & 極大 & \searrow \\ \end{array} \]
$M=f(1)=e^{-\frac{1}{4}}$
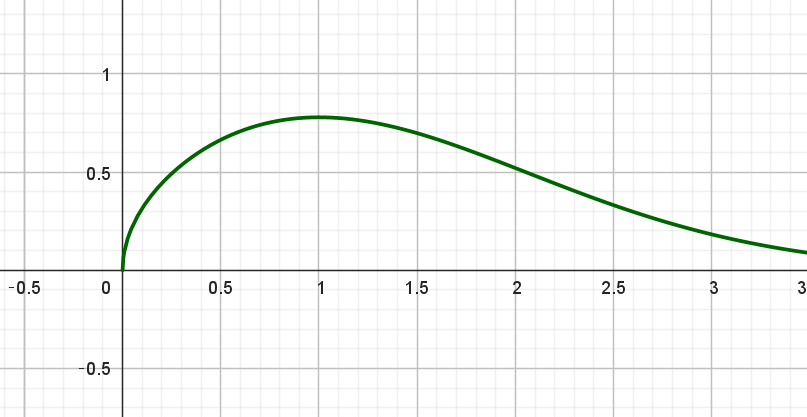
$なお、x \longrightarrow \infty \ \ のとき \ \ f(x) \longrightarrow 0 \ \ だから \ x\ 軸は漸近線$
$y=f(x)\ \ のグラフは右図のとおり$
(2)
(i)$\ \ e^{-\frac{25}{4}}\sqrt{x} \leqq f(x) \ \ (0 \leqq x \leqq 5 ) \ \ の証明$
\begin{eqnarray*} \quad & &f(x)-e^{-\frac{25}{4}}\sqrt{x}\\ \\ &=&\sqrt{x}e^{-\frac{x^2}{4}}-e^{-\frac{25}{4}}\sqrt{x}\\ \\ &=&\sqrt{x}(e^{-\frac{x^2}{4}}-e^{-\frac{25}{4}})\\ \end{eqnarray*} $\quad 0 \leqq x \leqq 5 \ \ において \ \ e^{-\frac{x^2}{4}} は単調減少だから \quad e^{-\frac{x^2}{4}} \geqq e^{-\frac{5^2}{4}}$
$\quad よって \quad f(x) \geqq e^{-\frac{25}{4}}\sqrt{x}$
(ii)$\ \ \dfrac{10}{3}f(5) \leqq \alpha \ \ の証明$
$\quad $(i)$\ \ より \quad e^{-\frac{25}{4}}\sqrt{x} \leqq f(x) \ \ (0 \leqq x \leqq 5 ) \ \ だから両辺積分して$
\[\quad \int_0^5e^{-\frac{25}{4}}\sqrt{x} dx \leqq \int_0^5f(x)dx\]
$\quad 右辺=\alpha $
\[\quad 左辺=e^{-\frac{25}{4}}\int_0^5\sqrt{x} dx=e^{-\frac{25}{4}}\big[\dfrac{2}{3}x^{\frac{3}{2}}\big]_0^5 =\dfrac{2}{3} \times 5\sqrt{5} \times e^{-\frac{25}{4}}=\dfrac{10}{3} \sqrt{5} e^{-\frac{25}{4}}=\dfrac{10}{3}f(5)\]
$\quad よって \quad \dfrac{10}{3}f(5) \leqq \alpha$
(3)
$\hspace{5em} \dfrac{2}{3}f(5) \leqq t \leqq f(5) \ \ のとき \hspace{12em} f(5) \leqq t \leqq M \ \ のとき$
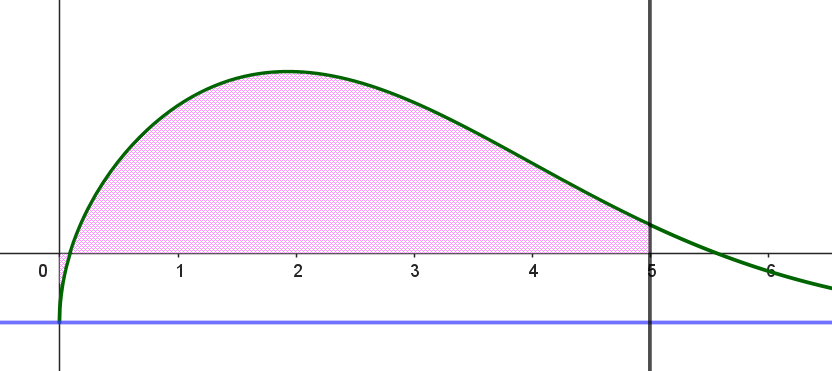
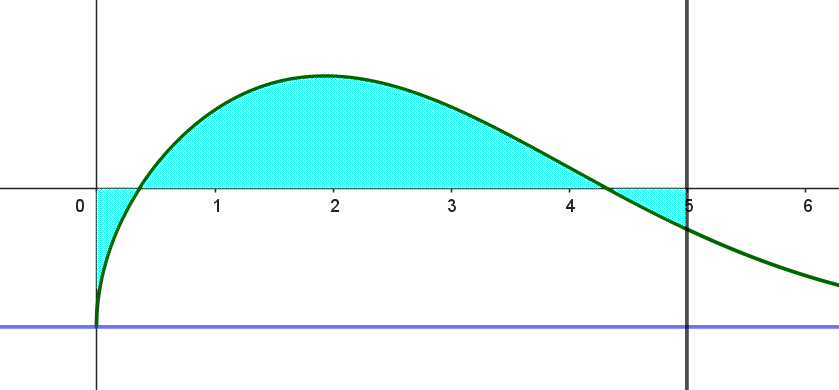
$どちらの場合も \ x\ 軸の周りに \ 1\ 回転させてできる回転体の体積V(t)\ は$
\begin{eqnarray*} V(t) &=&\pi\int_0^5(f(x)-t)^2dx\\ \\ &=&\pi\int_0^5(f(x)^2dx-2\pi t\int_0^5f(x)dx +\pi t^2\int_0^5dx\\ \\ &=&\pi\int_0^5(f(x)^2dx-2\pi \alpha t +5\pi t^2\\ \\ &=&5\pi(t^2-\dfrac{2\alpha}{5}t)+\pi\int_0^5(f(x)^2dx\\ \\ &=&5\pi(t-\dfrac{\alpha}{5})^2 - \dfrac{\pi \alpha ^2}{5} +\pi\int_0^5(f(x)^2dx\\ \end{eqnarray*}
$ここで、t=\dfrac{\alpha}{5} \ \ がとれるかどうか調べる。$
$(1)より \quad 0 \leqq x \leqq 5 \quad のとき \quad 0 \leqq f(x) \leqq M \quad だから$
\[\int_o^5f(x)dx \leqq \int_0^5Mdx=5M\]
$左辺=\alpha \ \ だから \quad \dfrac{\alpha}{5} \leqq M$
$(2)より \quad \dfrac{10}{3}f(5) \leqq \alpha \quad だから \quad \dfrac{2}{3}f(5) \leqq \dfrac{\alpha}{5} \leqq M$
$したがって \quad \dfrac{\alpha}{5}\ \ は区間\ [\dfrac{2}{3}f(5) , \ M ] \ の範囲に入っているから$
$V(t)\ は \ \ t=\dfrac{\alpha}{5}\ \ で最小となり、最小値は$
\begin{eqnarray*} V(\dfrac{\alpha}{5}) &=&- \dfrac{\pi \alpha ^2}{5} +\pi\int_0^5(f(x)^2dx\\ \\ &=&- \dfrac{\pi \alpha ^2}{5} +\pi\int_0^5 xe^{-\frac{x^2}{2}}dx\\ \\ &=&- \dfrac{\pi \alpha ^2}{5} +\pi\big[-e^{-\frac{x^2}{2}}\big]_0^5\\ \\ &=&- \dfrac{\pi \alpha ^2}{5} +\pi\big(1-e^{-\frac{25}{2}}\big)\\ \\ &=&\pi \big(1- e^{-\scriptsize{\dfrac{25}{2}}} - \dfrac{\alpha ^2}{5}\big)\\ \end{eqnarray*}
メインメニュー に戻る