筑波大学(理系) 2025年 問題5
$f(x)=\dfrac{\sin(\log x)}{x}\ \ (x > 1) \ \ について以下の問いに答えよ。$
$(1)\ \ f'(x),\ \ f''(x) \ \ を求めよ。$
$(2)\ \ n\ を正の整数とする。関数 \ f(x)\ が極大値をとる \ x\ で、e^{2(n-1)\pi} < x < e^{2n\pi}\ \ となるものがただ \ 1\ つ存在$
$\quad することを示せ。また、関数f(x)が極小値をとる \ x\ で、e^{2(n-1)\pi} < x < e^{2n\pi}\ \ となるものがただ \ 1\ つ存在$
$\quad することを示せ。$
$(3)\ \ 正の整数 \ n\ に対して、(2)の極大値をとる \ x\ を \ \alpha _n 、極小値をとる \ x\ を \ \beta _n \ とする。このとき$
\[\qquad \dfrac{1}{\pi}\Big\{\log \Big|\sum_{n=1}^{\infty} f''(\alpha_n)\Big|-\log \Big|\sum_{n=1}^{\infty} f''(\beta_n)\Big|\Big\}\]
$\quad は整数となる。その値を求めよ。$
(1)
$f(x)=\dfrac{\sin(\log x)}{x}\ \ (x > 1) \ \ より$
$f'(x)=\dfrac{\cos (\log x) \times \dfrac{1}{x} \times x -\sin(\log x)}{x^2}=\dfrac{\cos (\log x) -\sin(\log x)}{x^2}$
\begin{eqnarray*} f''(x) &=&\dfrac{\big\{-\sin (\log x) \times \dfrac{1}{x} -\cos(\log x) \times \dfrac{1}{x} \big\}x^2 -2x\big\{\cos (\log x) -\sin(\log x)\big\}}{x^4}\\ \\ &=&\dfrac{\big\{-\dfrac{1}{x}\sin (\log x) - \dfrac{1}{x}\cos(\log x) \big\}x -2\big\{\cos (\log x) -\sin(\log x)\big\}}{x^3}\\ \\ &=&\dfrac{-\sin (\log x) - \cos(\log x) -2(\cos (\log x) -\sin(\log x))}{x^3}\\ \\ &=&\dfrac{\sin (\log x) - 3\cos(\log x) }{x^3}\\ \end{eqnarray*}
(2)
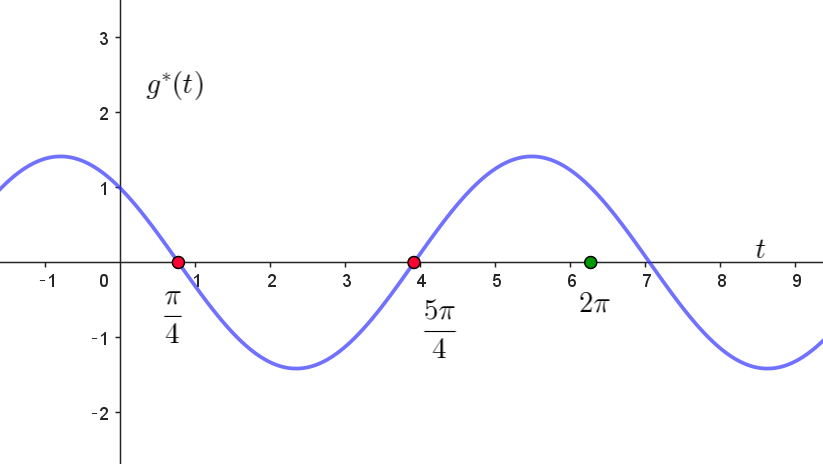
$f'(x)=0 \ \ より \quad g(x)=\cos (\log x) - \sin(\log x) =0$
$t=\log x \quad とおくと$
$g^*(t)=\cos t -\sin t =\sqrt{2}\cos(t+\dfrac{\pi}{4})$
$なお、g^*(t) \ は周期 \ \ 2\pi \ \ の周期関数$
$t=\log x \ \ は単調増加関数だから \ g^*(t)\ の増減と \ g(x)\ の増減は対応する。$
$g^*(t)=0 \ \ より \quad t=\dfrac{\pi}{4}+2n\pi,\quad \dfrac{5}{4}\pi + 2n\pi$
\[ \begin{array}{c||c|c|c|c|c} t& 0+2n\pi & \cdots & \dfrac{\pi}{4}+2n\pi & \cdots & \dfrac{5}{4}\pi +2n\pi& \cdots & 2(n+1)\pi\\ \hline g^*(t)& & + & 0 & - & 0 & + \\ \end{array} \]
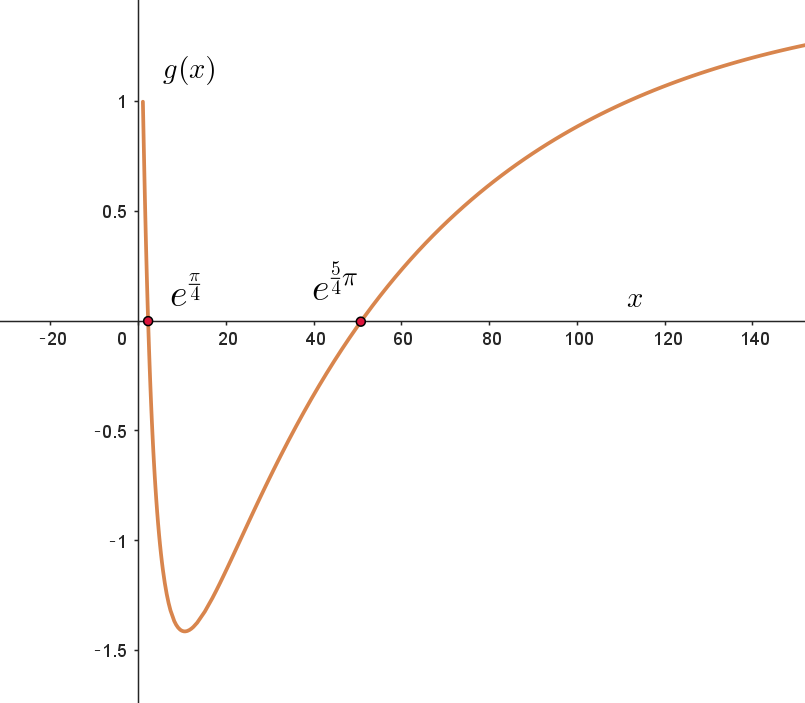
\[ \begin{array}{c||c|c|c|c|c} x& e^{2n\pi} & \cdots & e^{\scriptsize{\dfrac{\pi}{4}}+2n\pi} & \cdots & e^{\scriptsize{\dfrac{5}{4}}\pi+2n\pi} & \cdots & e^{2(n+1)\pi}\\ \hline g'(x)& & + & 0 & - & 0 & + \\ \hline g(x)& & \nearrow & 極大 & \searrow & 極小 & \nearrow \\ \end{array} \]
$あらためて、n \longrightarrow n-1 \quad とおくと$
$したがって、f(x)が極大値、極小値をとるxについて、$
$e^{2(n-1)\pi} < x < e^{2n\pi}\ \ でそれぞれただ \ 1\ つ存在する。$
(3)
$\alpha_n=e^{\scriptsize{\dfrac{\pi}{4}}+2n\pi} \quad だから \quad \log \alpha_n=\dfrac{\pi}{4}+2n\pi$
\begin{eqnarray*} f''(\alpha_n) &=&\dfrac{\sin (\log \alpha_n) - 3\cos(\log \alpha_n) }{\alpha_n^3}\\ \\ &=&\dfrac{\sin (\dfrac{\pi}{4}+2n\pi) - 3\cos(\dfrac{\pi}{4}+2n\pi) }{\big(e^{\scriptsize{\dfrac{\pi}{4}}+2n\pi} \big)^3}\\ \\ &=&\dfrac{\dfrac{\sqrt{2}}{2} - \dfrac{3\sqrt{2}}{2}}{e^{\scriptsize{\dfrac{3}{4}\pi}+6n\pi}}\\ \\ &=&-\dfrac{\sqrt{2}}{e^{\scriptsize{\dfrac{3}{4}\pi}+6n\pi}}\\ \end{eqnarray*}
$\beta_n=e^{\scriptsize{\dfrac{5}{4}\pi}+2n\pi} \quad だから \quad \log \beta_n=\dfrac{5}{4}\pi+2n\pi$
\begin{eqnarray*} f''(\beta_n) &=&\dfrac{\sin (\log \beta_n) - 3\cos(\log \beta_n) }{\beta_n^3}\\ \\ &=&\dfrac{\sin (\dfrac{5}{4}\pi+2n\pi) - 3\cos(\dfrac{5}{4}\pi+2n\pi) }{\big(e^{\scriptsize{\dfrac{5}{4}}\pi+2n\pi} \big)^3}\\ \\ &=&\dfrac{-\dfrac{\sqrt{2}}{2} + \dfrac{3\sqrt{2}}{2}}{e^{\scriptsize{\dfrac{15}{4}\pi}+6n\pi}}\\ \\ &=&\dfrac{\sqrt{2}}{e^{\scriptsize{\dfrac{15}{4}\pi}+6n\pi}}\\ \end{eqnarray*}
$よって$
\begin{eqnarray*} & &\dfrac{1}{\pi}\Big\{\log \Big|\sum_{n=1}^{\infty} f''(\alpha_n)\Big|-\log \Big|\sum_{n=1}^{\infty} f''(\beta_n)\Big|\Big\}\\ \\ &=&\dfrac{1}{\pi}\Big\{\log \sum_{n=1}^{\infty} \dfrac{\sqrt{2}}{e^{\scriptsize{\dfrac{3}{4}\pi}+6n\pi}}-\log \sum_{n=1}^{\infty}\dfrac{\sqrt{2}}{e^{\scriptsize{\dfrac{15}{4}\pi}+6n\pi}}\Big\}\\ \\ &=&\dfrac{1}{\pi}\Big\{\log \dfrac{\sqrt{2}}{e^{\scriptsize{\dfrac{3}{4}\pi}}} \sum_{n=1}^{\infty} e^{-6n\pi}-\log \dfrac{\sqrt{2}}{e^{\scriptsize{\dfrac{15}{4}\pi}}}\sum_{n=1}^{\infty}e^{-6n\pi}\Big\}\\ \\ &=&\dfrac{1}{\pi}\Big\{\log \sqrt{2} \sum_{n=1}^{\infty} e^{-6n\pi} -\log e^{\scriptsize{\dfrac{3}{4}\pi}} - \log \sqrt{2} \sum_{n=1}^{\infty} e^{-6n\pi} + \log e^{\scriptsize{\dfrac{15}{4}\pi}} \Big\} \hspace{5em}(☆)\\ \\ &=&\dfrac{1}{\pi}\Big\{-\log e^{\scriptsize{\dfrac{3}{4}\pi}} + \log e^{\scriptsize{\dfrac{15}{4}\pi}} \Big\}\\ \\ &=&\dfrac{1}{\pi}\Big\{-\dfrac{3}{4}\pi+ \dfrac{15}{4}\pi \Big\}\\ \\ &=&3 \end{eqnarray*} $なお、(☆)の無限和は \ \ 公比=e^{-6\pi}\ \ だから \ \ 0 < 公比 < 1 \ \ の無限等比級数、したがって収束して和をもつ$
\[\sum_{n=1}^{\infty} e^{-6n\pi}=\sum_{n=1}^{\infty} \big(e^{-6\pi}\big)^n =\dfrac{e^{-6\pi}}{1-e^{-6\pi}} \quad これは有限な値である。\]
メインメニュー に戻る