筑波大学(理系) 2023年　問題1


$曲線 \ C:\ y=x-x^3 \ \ 上の点 \ A(1,\ 0)\ における接線を \ \ell\ とし、C\ と \ \ell\ の共有点のうち \ A\ と異なる点を$
$B\ とする。また、-2 < t < 1 \ \ とし、C\ 上の点 \ P(t,\ t-t^3)\ をとる。さらに、三角形 \ ABP\ の面積を$
$S(t)\ とする。$
$(1)\ \ 点 \ B\ の座標を求めよ。$
$(2)\ \ S(t)\ を求めよ。$
$(3)\ \ t\ が \ -2 < t < 1\ の範囲を動くとき、S(t)\ の最大値を求めよ。$


(1)

　

$y=x-x^3=-x(x+1)(x-1) \quad は \ \ x\ 軸と \ 3\ 点 \ (1,\ 0),\ (0,\ 0),\ (-1,\ 0)\ で$

$交わる \ 3\ 次関数だからグラフは右図のとおりである。$

$y'=1-3x^2 \quad だから \quad x=1 \ \ のとき \ \ y'=-2$

$A(1,\ 0)\ における接線 \ \ell \ は \quad y=-2(x-1)$

$曲線 \ C と \ \ell\ の共有点のうち \ A\ と異なる点は$

$-x(x+1)(x-1)=-2(x-1) \quad より \quad (x-1)(x(x+1)-2)=0$

$(x-1)(x^2+x-2)=0 \qquad (x-1)^2(x+2)=0$

$x \ne 1 \ \ だから \quad x=-2$

$このとき \quad y=-2-(-2)^3=6$

$よって \quad B(-2,\ 6)$


(2)

　

$接線 \ \ell \ は \ \ y=-2(x-1)\ \ すなわち \ \ 2x+y-2=0$

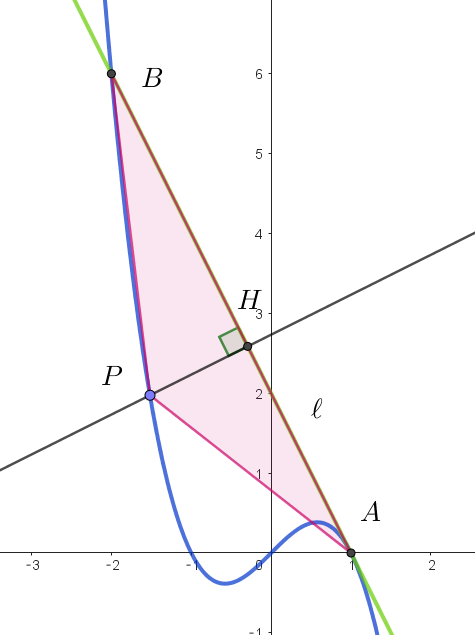
$-2 < t < 1 \ \ だから \ C\ 上の点 \ P(t,\ t-t^3)\ は直線 \ \ell \ の下側、$

$すなわち原点のある側にあり、負領域にある。$

$したがって、点 \ Pから直線 \ \ell :\ 2x+y-2=0 \ \ に下ろした垂線の長さ \ PH \ は$

$PH=-\cfrac{2t+(t-t^3)-2}{\sqrt{2^2+1^2}}=\cfrac{1}{\sqrt{5}}(t^3-3t+2)$

\begin{eqnarray*} S(t) &=&\cfrac{1}{2}\times AB \times PH\\ \\ &=&\cfrac{1}{2} \times \sqrt{(1+2)^2+(0-6)^2} \times \cfrac{1}{\sqrt{5}}(t^3-3t+2)\\ \\ &=&\cfrac{3}{2} (t^3-3t+2)\\ \end{eqnarray*}

(3)


$S'(t)=\cfrac{3}{2} (3t^2-3)=\cfrac{9}{2}(t+1)(t-1)$

$S'(t)=0 \ \ の解は \ \ -2 < t < 1 \ \ だから \quad t=-1$

$S(-2)=0, \quad S(1)=0$

$増減表は$

　

\[ \begin{array}{c||c|c|c|c|c} t & -2 & \cdots & -1 & \cdots & 1\\ \hline S'(t)& & + & 0 & - & & \\ \hline S(t)& 0 & \nearrow & 極大 & \searrow & 0 &\\ \end{array} \]
$t=-1 \ で \ S(t)\ は極大かつ最大となり、最大値は$

$S(-1)=\cfrac{3}{2}((-1)^3 -3 \times (-1) +2=6$




ページの先頭へ↑




メインメニュー　に戻る