筑波大学(理系) 2021年 問題6
$i\ は虚数単位とする。複素数平面において、複素数 \ z\ の表す点 \ P\ を \ P(z)\ または点 \ z\ と書く。$
$\omega =-\cfrac{1}{2}+\cfrac{\sqrt{3}}{2}i\ \ とおき、3\ 点 \ A(1),\ B(\omega),\ C(\omega ^2)\ を頂点とする \ \triangle ABC \ \ を考える。$
$(1)\ \ \triangle ABC \ \ は正三角形であることを示せ。$
$(2)\ \ 点 \ z\ が辺 \ AC\ 上を動くとき、点 \ -z\ が描く図形を複素数平面上に図示せよ。$
$(3)\ \ 点 \ z\ が辺 \ AB\ 上を動くとき、点 \ z^2\ が描く図形を \ E_1\ とする。また、点 \ z\ が辺 \ AC\ 上を動くとき、$
$\qquad 点 \ z^2\ が描く図形を \ E_2\ とする。E_1\ と \ E_2\ の共有点をすべて求めよ。$
$(解説)$
$(1)\ \ 3\ つの内角を調べるか、3\ 辺の長さを求めるかの \ 2\ 通りの方法が考えられます。$
$(2)\ \ z\ と \ -z\ の位置関係を考えます。$
$(3)\ \ E_1\ と \ E_2\ の共有点は \ \ z_1^2=z_2^2\ \ を満たす点だから\ z_1=\pm z_2\ となるので、これから \ 2\ 線分の交点を求めます。$
(1)
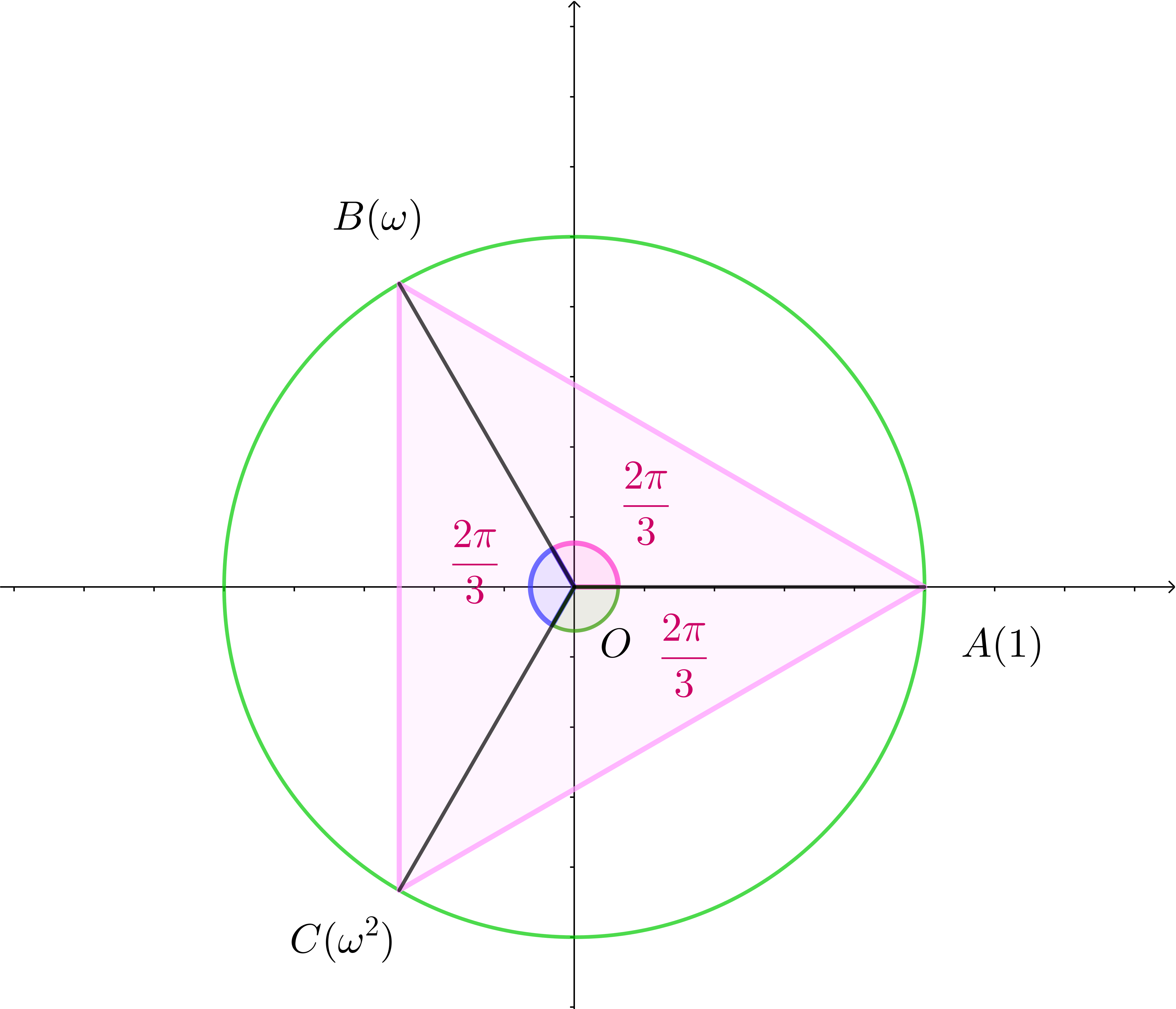
$\omega=\cos \cfrac{2\pi}{3}+i\sin \cfrac{2\pi}{3} \ \ だから点 \ B(\omega)\ は \ A(1)\ を原点のまわりに$
$\cfrac{2\pi}{3}\ 回転した点で、点 \ C(\omega ^2)\ は点 \ B(\omega)\ を原点のまわりに \ \cfrac{2\pi}{3}$
$回転した点である。$
$したがって、3\ 点 \ A,\ B,\ C\ は原点を中心とした、半径 \ 1\ の$
$円周上にある。$
$円周角の定理より、\angle A=\angle B=\angle C=\cfrac{\pi}{3} \quad だから$
$\triangle ABC \ \ は正三角形である。$
$(別解)$
$\vec{AB}=\omega -1=\big(-\cfrac{1}{2}+\cfrac{\sqrt{3}}{2}i\big)-1=-\cfrac{3}{2}+\cfrac{\sqrt{3}}{2}i$
$|\vec{AB}|^2=\big(-\cfrac{3}{2}\big)^2 +\big(\cfrac{\sqrt{3}}{2}\big)^2=3 \qquad \therefore \ \ AB=\sqrt{3}$
$\quad |\omega -1|=\sqrt{3} ,\qquad |\omega|=\big|-\cfrac{1}{2}+\cfrac{\sqrt{3}}{2}i\big|=1,\qquad \omega ^3=1 \quad をつかって$
$\vec{BC}=\omega ^2-\omega =\omega (\omega -1) \quad だから \quad |\vec{BC}|=|\omega| |\omega -1|=\sqrt{3} \qquad BC=\sqrt{3}$
$\vec{CA}=1-\omega ^2 =\omega ^3-\omega ^2=\omega ^2 (\omega -1) \quad だから \quad |\vec{CA}|=|\omega |^2 |\omega -1|=\sqrt{3} \qquad CA=\sqrt{3}$
$したがって \quad AB=BC=CA \quad だから \quad \triangle ABC \ \ は正三角形である。$
(2)
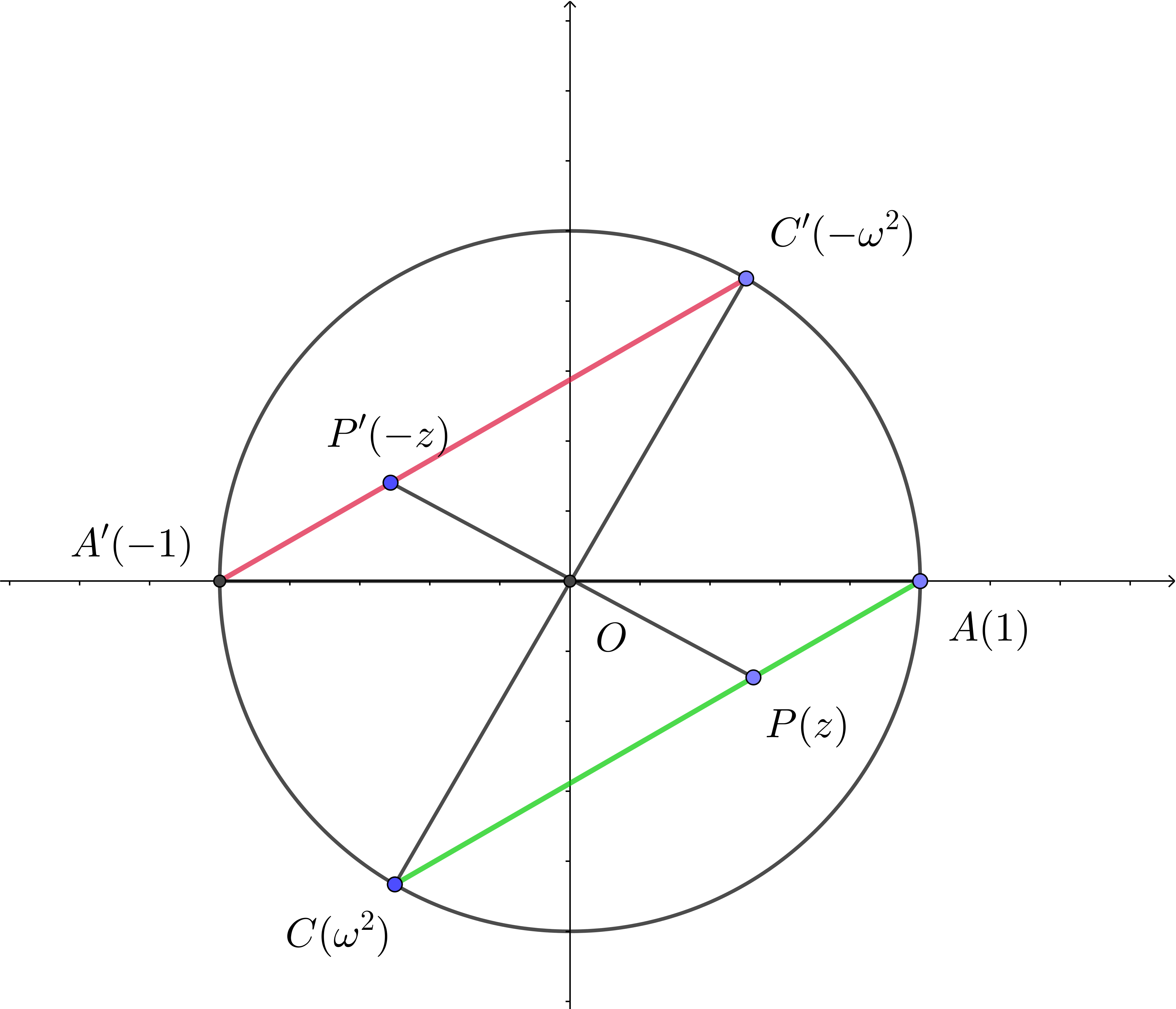
$点 \ P(z)\ と点 \ P'(-z)\ の位置関係は原点について対称である。$
$A(1)\ の対称点は \ A'(-1),\quad C(\omega ^2)\ の対称点は \ C'(-\omega ^2)$
$一般に点に関する対称変換では、線分は線分に移るから$
$線分 \ AC\ は右図の赤い線分 \ A'C'\ に移る。$
(3)
$辺 \ AB\ 上を動く点を \ z_1、辺 \ AC\ 上を動く点を \ z_2\ とおく。$
$E_1\ と \ E_2\ の共有点は \ \ z_1^2=z_2^2\ \ を満たす点だから \qquad z_1=\pm z_2$
(i)$\ \ z_1=z_2 \quad のとき$
$\quad 線分 \ AB\ と線分 \ AC\ の交点だから \ \ A(1),\ すなわち \ \ z_1=z_2=1\ \ のときで、z_1^2=z_2^2=1$
(ii)$\ \ z_1=-z_2 \quad のとき$
$\quad z_1=1-t+t\omega ,\quad z_2=1-s+s\omega ^2 \ \ (s,\ t\ は実数)\quad とおけるから$
$\quad 1-t+t\omega=-(1-s +s\omega ^2)$
$\quad 1-t+t\omega=-1+s -s(-1 - \omega) $
\[ \hspace{1em} \left\{ \begin{array}{l} 1-t=-1+2s\\ t=s\\ \end{array} \right. \] $\quad これを解いて \quad t=s=\cfrac{2}{3}$
$よって$
$\quad z_1=1-\cfrac{2}{3}+\cfrac{2}{3}\omega=\cfrac{1}{3}+\cfrac{2}{3} \times \big(-\cfrac{1}{2}+\cfrac{\sqrt{3}}{2}i\big)=\cfrac{\sqrt{3}}{3}i$
$\quad z_2=1-\cfrac{2}{3}+\cfrac{2}{3}\omega^2=\cfrac{1}{3}+\cfrac{2}{3} \times \big(-\cfrac{1}{2}-\cfrac{\sqrt{3}}{2}i\big)=-\cfrac{\sqrt{3}}{3}i$
$なお、(2)より、点 \ (-z_2)\ は点 \ A(1),\ C(\omega ^2)\ を原点について対称移動した点 \ A'(-1),\ C'(-\omega ^2)\ の線分 \ A'C'\ 上にある。$
$線分 \ AB\ と \ A'C'\ の交点が \ z=\cfrac{\sqrt{3}}{3}i\ \ である。$
$同様に、点(-z_1)\ は点 \ A(1),\ B(\omega )\ を原点について対称移動した点 \ A'(-1),\ B'(-\omega )\ の線分 \ A'B'\ 上にある。$
$線分 \ AC\ と \ A'B'\ の交点が \ z=-\cfrac{\sqrt{3}}{3}i\ \ である。$
$いずれにせよ \qquad z_1^2=z_2^2=-\cfrac{1}{3}$
(i),(ii)$より \quad E_1 \ と \ E_2\ の共有点は \quad z=1 \ \ と \ \ z=-\cfrac{1}{3}$
$(研究)$
$図形E_1とE_2 を具体的に求めてみましょう。$
$簡単になるように、複素数平面は、座標軸を平行移動して、虚軸は \ \omega \ を単位とした軸とします。$
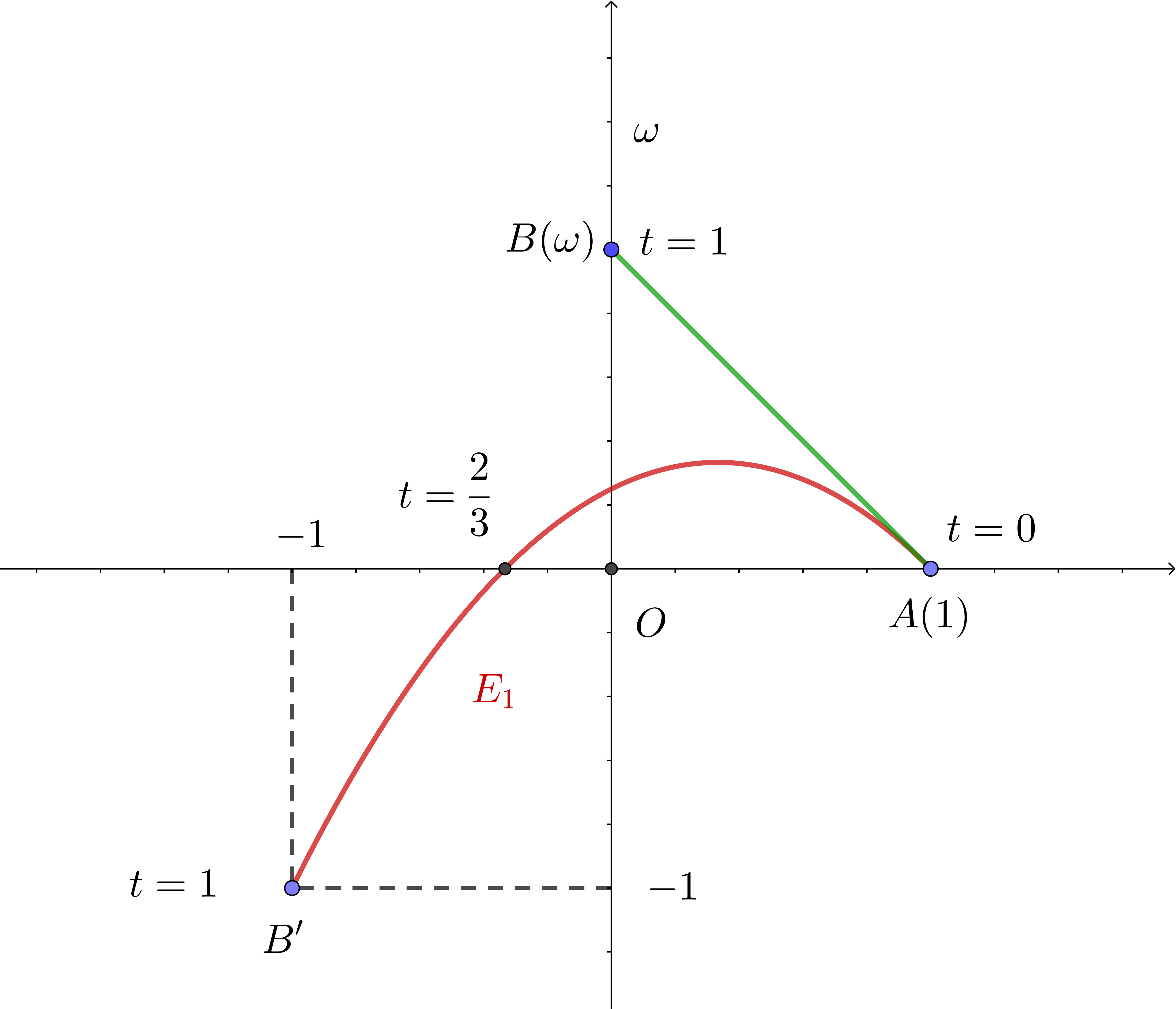
(i)$\ \ E_1\ について$
$\quad 線分 \ AB\ は \quad z=1-t +t \omega \ \ (0 \leqq t \leqq 1)\quad と表せるから \quad \omega^2+\omega +1=0 \ \ をつかって$
\begin{eqnarray*} z^2 &=& (1-t)^2 + 2t(1-t)\omega + t^2\omega ^2\\ \\ &=& (1-t)^2 + 2t(1-t)\omega + t^2(-\omega -1)\\ \\ &=& 1-2t + (-3t^2+2t)\omega \\ \end{eqnarray*} $\quad x=1-2t ,\quad y=-3t^2+2t \quad とおき、t=\cfrac{1-x}{2} \quad を \ y\ に代入すると$
\begin{eqnarray*}
y
&=&-3\big(\cfrac{1-x}{2}\big)^2+ 1-x\\
\\
&=&-\cfrac{3}{4}x^2+\cfrac{1}{2}x+\cfrac{1}{4}\\
\\
&=&-\cfrac{3}{4}\big(x-\cfrac{1}{3}\big)^2+\cfrac{1}{3}\\
\end{eqnarray*}
$\quad 0 \leqq t \leqq 1 \quad だから \quad 0 \leqq \cfrac{1-x}{2} \leqq 1 \quad より \quad -1 \leqq x \leqq 1$
$\quad t=0 \ \ のとき \quad z^2=1 \ \ (x=1,\ y=0) ,\qquad t=1 \ \ のとき \quad z^2=-1 -\omega \ \ (x=-1,\ y=-1) \ \ である。$
$\quad 図形 \ E_1\ は放物線で、グラフは右図のとおりである。$
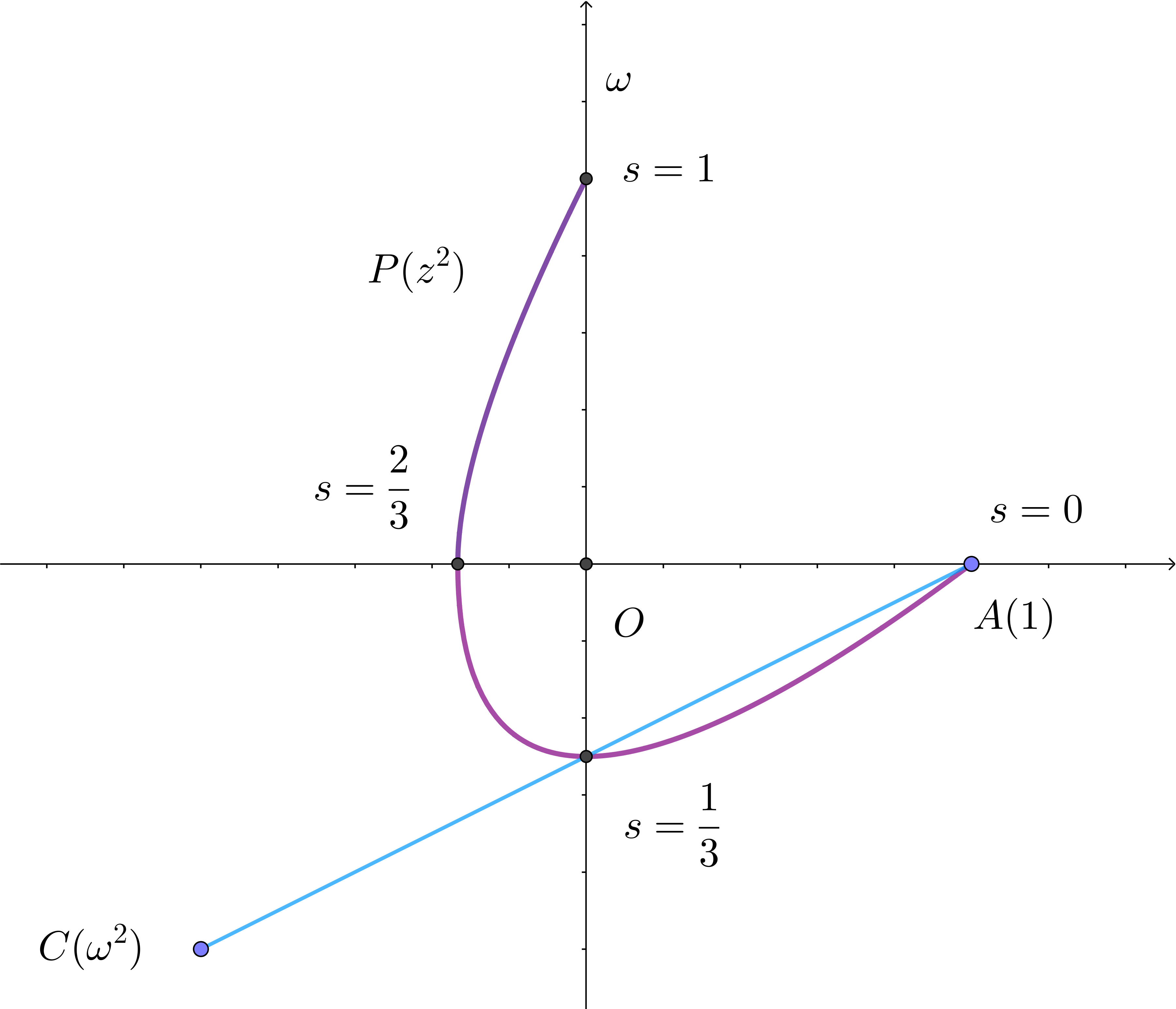
(ii)$\ \ E_2\ について$
$\quad 線分 \ AC\ は \ \ z=1-s +s \omega ^2 \ \ (0 \leqq s \leqq 1)\ と表せるから$
$\qquad z=1-s+s(-\omega -1)=1-2s-s\omega$
\begin{eqnarray*}
z^2
&=& (1-2s)^2 - 2s(1-2s)\omega + s^2\omega ^2\\
\\
&=& (1-2s)^2 - 2s(1-2s)\omega + s^2(-\omega -1 )\\
\\
&=& 3s^2-4s +1 + (3s^2 - 2s)\omega \\
\end{eqnarray*}
$\qquad x=3s^2-4s +1 \hspace{10em}①$
$\qquad y=3s^2 -2s \hspace{12em}②$
$\quad ①-②\ \ より \quad x-y=-2s+1 \qquad s=\cfrac{1}{2}(-x+y+1) \quad これを②に代入して$
$\quad y=3 \times \cfrac{1}{4}(-x+y+1)^2 -2 \times \cfrac{1}{2}(-x+y+1) $
$\quad 4y=3(-x+y+1)^2 -4(-x+y+1) $
$\quad 3x^2-6xy +3y^2-2x-2y-1=0$
$\quad この2次曲線は、判別式 \ \ \cfrac{D}{4}=9 -3 \times 3=0$
$\quad より放物線である。$
$\quad このことについては($2次曲線の標準化$)を参考にしてください。$
$\quad 図形 \ E_2のグラフは右図のとおりである。$
(iii)$\ \ E_1 とE_2の共有点について$
$\quad 1-2t + (-3t^2+2t)\omega =3s^2-4s +1 + (3s^2 - 2s)\omega \quad より$
\[
\hspace{1em}
\left\{ \begin{array}{l}
1-2t=3s^2-4s+1 \hspace{5em}③\\
-3t^2+2t=3s^2-2s \hspace{5em}④\\
\end{array} \right.
\]
$\quad ③より \quad t=-\cfrac{3s^2-4s}{2} \quad これを④に代入して$
$\quad -3\big(-\cfrac{3s^2-4s}{2}\big)^2+2\big(-\cfrac{3s^2-4s}{2}\big)=3s^2-2s$
$\quad 9s^4-24s^3+24s^2-8s=0$
$\quad s(3s-2)(3s^2-6s+4)=0$
$\quad 3s^2-6s+4=3(s-1)^2+1 > 0 \quad だから\ \ 解は \quad s=0,\ \ \cfrac{2}{3}$
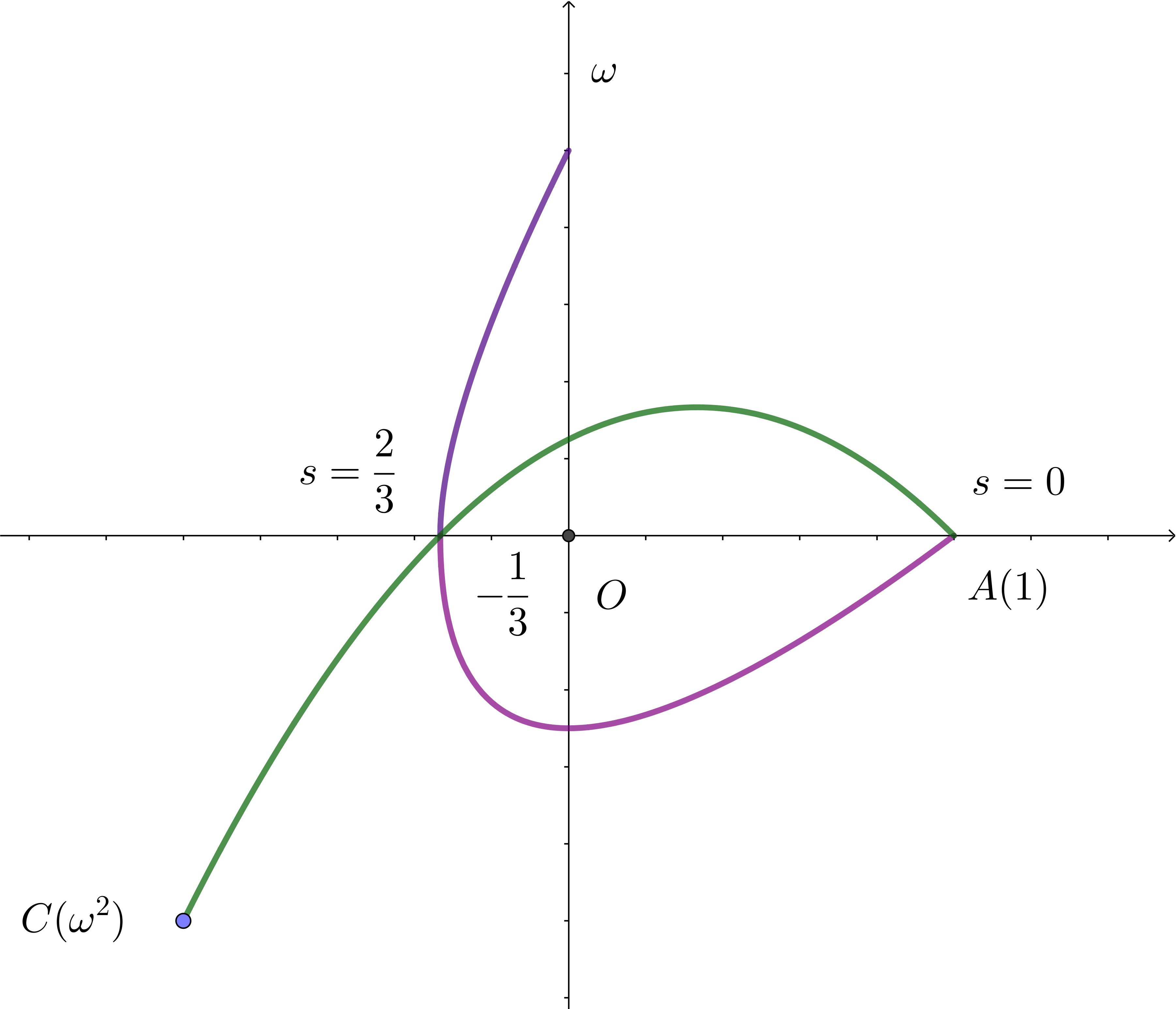
$\quad それぞれ \ \ $(ii)$\ \ の① \ ②に代入して$
$\quad s=0\ \ のとき \quad x=1,\ \ y=0 $
$\quad s=\cfrac{2}{3}\ \ のとき \quad x=-\cfrac{1}{3},\ \ y=0 $
$\quad したがって \quad E_1 \ と \ E_2\ の共有点は \quad z=1 \ \ と \ \ z=-\cfrac{1}{3}$
$(補充)$
(iii)$で\ \ E_1\ と \ E_2\ の共有点について$
$\quad 1-2t + (-3t^2+2t)\omega =3s^2-4s +1 + (3s^2 - 2s)\omega \quad より$
\[
\hspace{1em}
\left\{ \begin{array}{l}
1-2t=3s^2-4s+1\\
-3t^2+2t=3s^2-2s \\
\end{array} \right.
\]
$\quad としたが、その根拠は$
$a,\ b,\ c,\ d\ が実数のとき$
$\qquad a+b\omega=c+d\omega \quad \Longleftrightarrow \quad a=c \ \ かつ \ \ b=d$
$\ \ \Longrightarrow \quad の証明$
$\qquad a+b\omega=c+d\omega $
$\qquad a -c +(b-d)\omega=0$
$\qquad a-c +(b-d) \times \cfrac{-1+\sqrt{3}i}{2}=0$
$\qquad 2(a-c) +(b-d) (-1+\sqrt{3}i)=0$
$\qquad (2a-2c -b + d)+\sqrt{3}(b-d)i=0$
$\qquad 2a-2c -b + d=0 \quad かつ \quad b-d =0$
$\quad よって \quad a=c,\quad b=d$
$\quad \ \ \Longleftarrow \quad の証明は明らか$
メインメニュー に戻る