MY MATH NOTE

筑波大学(理系) 2021年　問題5

$O\ を原点とする \ xy\ 平面において、点 \ A(-1,\ 0)\ と点 \ B(2,\ 0)\ をとる。円\ \ x^2+y^2=1\ \ の、x \geqq 0\ \ かつ$
$y \geqq 0\ \ を満たす部分を \ C\ とし、また点 \ B\ を通り \ y\ 軸に平行な直線を \ l\ とする。2\ 以上の整数 \ n\ に対し、$
$曲線 \ C\ 上に点 \ P,\ Q\ を \ \angle POB=\cfrac{\pi}{n},\ \ \angle QOB=\cfrac{\pi}{2n}\ を満たすようにとる。直線 \ AP\ と直線 \ l\ の交点をV$
$とし、直線 \ AQ\ と直線 \ l\ の交点を \ W\ とする。線分 \ AP、線分 \ AQ\ および曲線 \ C\ で囲まれた図形の面積$
$をS(n)\ とする。また線分 \ PV,\ 曲線 \ QW,\ 曲線 \ C\ および線分 \ VW\ で囲まれた図形の面積を \ T(n)\ とする。$
\[(1)\ \lim_{n \rightarrow \infty} n\{S(n)+T(n)\}\ \ を求めよ。\] \[(2)\ \lim_{n \rightarrow \infty} \cfrac{T(n)}{S(n)}\ \ を求めよ。\]

(1)

　
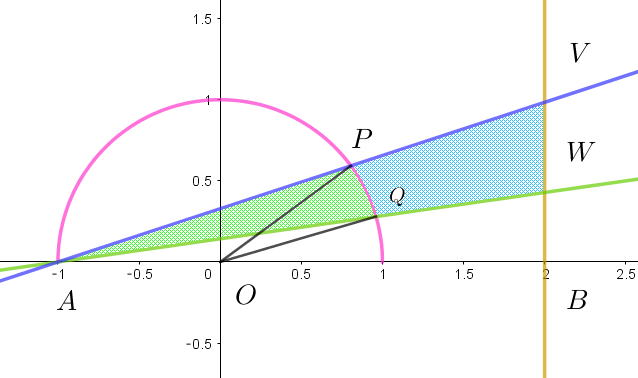
$P(\cos \cfrac{\pi}{n},\ \sin \cfrac{\pi}{n}),\quad Q(\cos \cfrac{\pi}{2n},\ \sin \cfrac{\pi}{2n})\ \ で$

$直線 \ APは、傾き \quad \cfrac{\sin \dfrac{\pi}{n}}{1+\cos \dfrac{\pi}{n}},\quad A(-1,\ 0)\ \ を通るから$
$\quad y=\cfrac{\sin \dfrac{\pi}{n}}{1+\cos \dfrac{\pi}{n}} (x+1)$

$\quad x=2\ \ のとき \quad y=\cfrac{3\sin \dfrac{\pi}{n}}{1+\cos \dfrac{\pi}{n}} \quad だから \quad V\Big(2,\ \cfrac{3\sin \dfrac{\pi}{n}}{1+\cos \dfrac{\pi}{n}}\Big)$

$直線 \ AQは、傾き \quad \cfrac{\sin \dfrac{\pi}{2n}}{1+\cos \cfrac{\pi}{2n}},\quad A(-1,\ 0)\ \ を通るから \qquad y=\cfrac{\sin \cfrac{\pi}{2n}}{1+\cos \cfrac{\pi}{2n}} (x+1)$

$\qquad x=2\ \ のとき \quad y=\cfrac{3\sin \dfrac{\pi}{2n}}{1+\cos \dfrac{\pi}{2n}} \quad だから \quad W\Big(2,\ \cfrac{3\sin \dfrac{\pi}{2n}}{1+\cos \dfrac{\pi}{2n}}\Big)$

$よって \qquad VW=\cfrac{3\sin \dfrac{\pi}{n}}{1+\cos \cfrac{\pi}{n}} - \cfrac{3\sin \dfrac{\pi}{2n}}{1+\cos \dfrac{\pi}{2n}}$

$\therefore \triangle AVW=\cfrac{1}{2} \times VW \times AB=\cfrac{3}{2}\Big(\cfrac{3\sin \dfrac{\pi}{n}}{1+\cos \dfrac{\pi}{n}} - \cfrac{3\sin \dfrac{\pi}{2n}}{1+\cos \dfrac{\pi}{2n}}\Big)$

$ここで、\cfrac{\pi}{2n}=\theta \quad とおくと$

\begin{eqnarray*} \triangle AVW &=&\cfrac{3}{2}\Big(\cfrac{3\sin 2\theta}{1+\cos 2\theta} - \cfrac{3\sin \theta }{1+\cos \theta} \Big)\\ \\ &=&\cfrac{9}{2}\Big(\cfrac{2\sin \theta \cos \theta }{2\cos ^2\theta} - \cfrac{3\sin \theta }{1+\cos \theta} \Big)\\ \\ &=&\cfrac{9}{2}\sin \theta \big(\cfrac{1}{\cos \theta} - \cfrac{1}{1+\cos \theta} \big)\\ \\ &=&\cfrac{9}{2}\sin \theta \times \cfrac{1}{\cos \theta (1+\cos \theta)}\\ \\ &=&\cfrac{9\tan \theta}{2(1+\cos \theta)}\\ \end{eqnarray*} $したがって$

\begin{eqnarray*} & &\lim_{n \rightarrow \infty} n\{S(n)+T(n)\}\\ \\ &=&\lim_{n \rightarrow \infty} n \triangle AVW\\ \\ &=&\lim_{\theta \rightarrow 0} \cfrac{\pi}{2\theta }\times \cfrac{9\tan \theta}{2(1+\cos \theta)}\\ \\ &=&\cfrac{9}{4}\pi \lim_{\theta \rightarrow 0} \cfrac{\tan \theta}{\theta}\cdot \cfrac{1}{1+\cos \theta}\\ \\ &=&\cfrac{9}{4}\pi \times 1 \times \cfrac{1}{2}\\ \\ &=&\cfrac{9}{8}\pi\\ \end{eqnarray*}

(2)

　
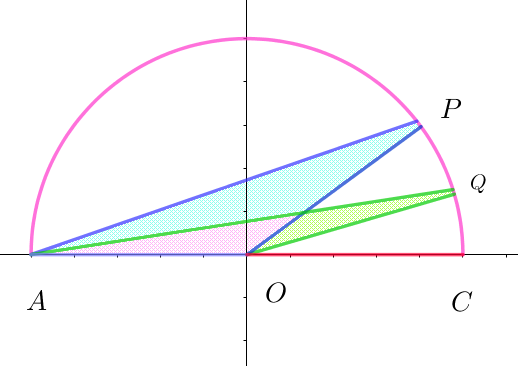
\begin{eqnarray*} S(n) &=&図形APC - 図形AQC\\ \\ &=&(\triangle OAP + 扇形OPC) - (\triangle OAQ + 扇形OQC)\\ \\ &=&(\cfrac{1}{2}\sin (\pi -\dfrac{\pi}{n}) + \dfrac{\pi}{2n})- (\cfrac{1}{2}\sin (\pi -\dfrac{\pi}{2n}) + \dfrac{\pi}{4n})\\ \\ &=&\cfrac{1}{2}(\sin \dfrac{\pi}{n} - \sin \dfrac{\pi}{2n}) + \cfrac{\pi}{4n} \\ \\ &=&\cfrac{1}{2}(\sin 2\theta - \sin \theta ) + \cfrac{\theta}{2} \\ \\ &=&\cfrac{1}{2}\{\sin \theta (2\cos \theta -1)+ \theta\} \\ \end{eqnarray*}
$よって$
\begin{eqnarray*} \lim_{n \rightarrow \infty}\cfrac{T(n)}{S(n)} &=&\lim_{n \rightarrow \infty}\cfrac{\triangle AVW - S(n)}{S(n)}\\ \\ &=&\lim_{n \rightarrow \infty}\cfrac{\triangle AVW }{S(n)}-1\\ \\ &=&\lim_{\theta \rightarrow 0}\cfrac{9\tan \theta}{2(1+\cos \theta)} \times \cfrac{2}{\sin \theta (2\cos \theta -1)+ \theta } -1\\ \\ &=&\lim_{\theta \rightarrow 0}9 \times \cfrac{\tan \theta}{\theta} \times \cfrac{1}{1+\cos \theta } \times \cfrac{1}{\cfrac{\sin \theta}{\theta}(2\cos \theta -1)+ 1} -1\\ \\ &=&\ \ 9 \times 1 \times \cfrac{1}{2} \times \cfrac{1}{1 \times 1 +1}-1\\ \\ &=&\cfrac{5}{4} \end{eqnarray*}

ページの先頭へ↑