筑波大学(理系) 2021年 問題4
$p,\ q\ を定数とし、0 < p < 1\ \ とする。曲線 \ C_1:y=px^{\scriptsize{\cfrac{1}{p}}}\ \ (x > 0)\ と、曲線 \ C_2:y=\log x + q \ \ (x > 0)\ が、ある$
$1\ 点 \ (a,\ b)\ において同じ直線に接するとする。曲線 \ C_1、直線 \ x=a,\ 直線 \ x=e^{-q}\ および \ x\ 軸で囲まれた$
$図形の面積を \ S_1\ とする。また、 曲線 \ C_2、直線 \ x=a,\ および \ x\ 軸で囲まれた図形の面積を \ S_2\ とする。$
$(1)\ \ q\ を \ p\ を用いて表せ。$
$(2)\ \ S_1,\ S_2\ を \ p\ を用いて表せ。$
$(3)\ \ \cfrac{S_2}{S_1} \geqq \cfrac{3}{4} \ \ であることを示せ。ただし、2.5 < e <3 \ \ を用いてよい。$
$(解説)$
$(1)\ \ ある点において同じ直線に接するとは、関数値が等しく、かつ微分係数が等しいことです。$
$(2)\ \ (1)より \ S_1\ と \ S_2\ を求める \ 2\ つの積分区間は一致し、面積は \ p\ で表すことができます。$
$(3)\ \ \cfrac{S_2}{S_1}\ \ を微分して最小値が \ \ \cfrac{3}{4}\ \ であることを示そうとしても、挫折します。$
$\qquad 不等式が与えられていますので、これを変形して \ \ 4S_2-3S_1 >0 \ \ を示した方が楽です。ところが、$
$\qquad これもなかなかうまくいきません。ポイントは \ \ e < 3 \ \ をどこで、どのようにつかうかです。$
(1)
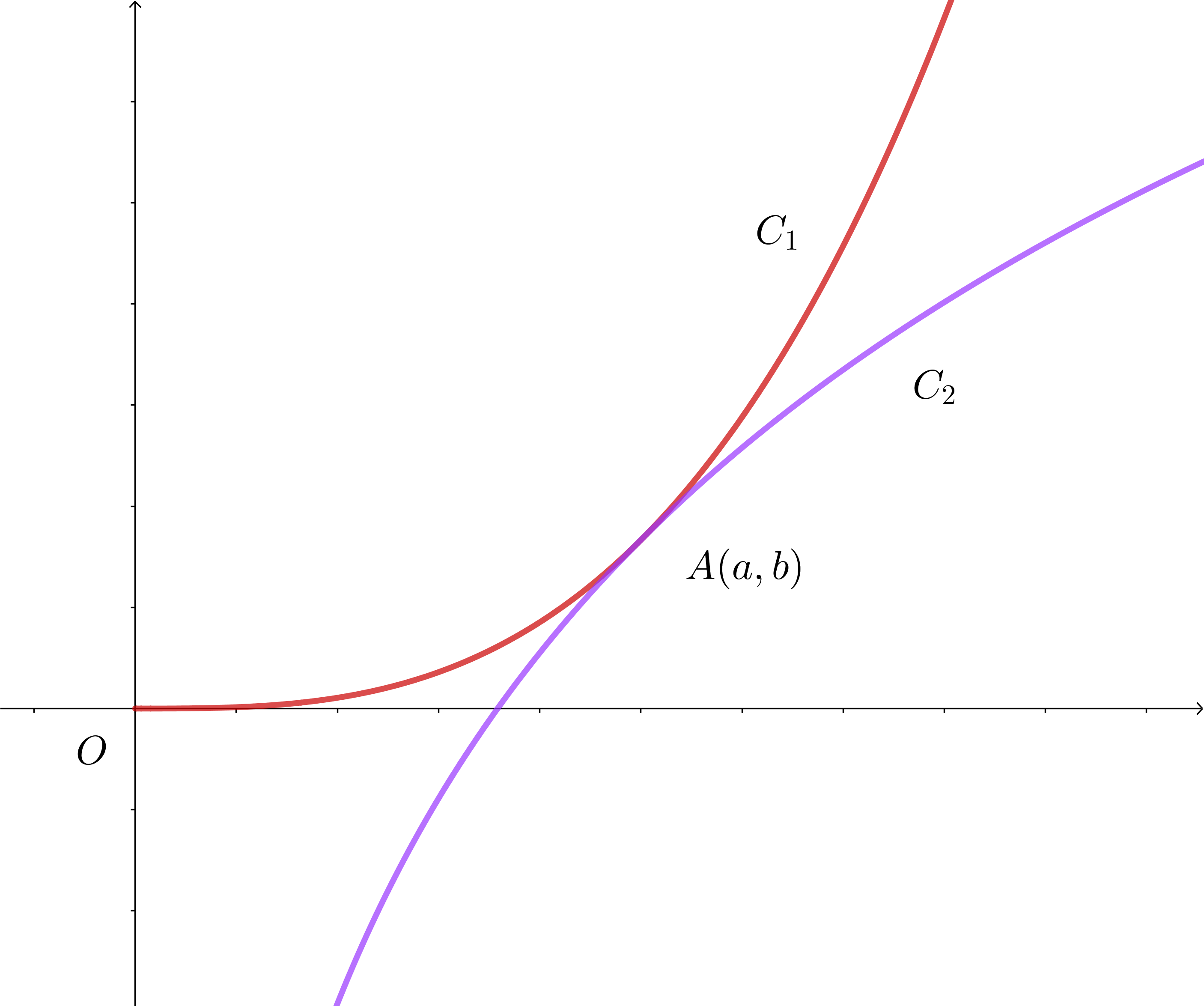
$点 \ (a,\ b)\ において同じ値をもつから \quad pa^{\scriptsize{\cfrac{1}{p}}}=\log a + q \hspace{5em}①$
$2\ つの曲線の関数の導関数は \quad y'=x^{\scriptsize{\cfrac{1}{p}}-\normalsize{1}} ,\qquad y'=\cfrac{1}{x} $
$点 \ (a,\ b)\ において同じ微分係数をもつから \quad a^{\scriptsize{\cfrac{1}{p}}-\normalsize{1}}=\cfrac{1}{a} $
$\quad a a^{\scriptsize{\cfrac{1}{p}}-\normalsize{1}}=1,\qquad a^{\scriptsize{\cfrac{1}{p}}}=1 \qquad 両辺 \ p\ 乗して \quad a=1$
$\quad ①に代入して \qquad p=\log 1 +q=q \qquad \therefore \ \ q=p$
(2)
$\qquad a=1,\quad e^{-q}=e^{-p} \quad だから$
\begin{eqnarray*} S_1 &=&\int_{e^{-q}}^a px^{\scriptsize{\cfrac{1}{p}}}dx\\ \\ &=&\int_{e^{-p}}^1 px^{\scriptsize{\cfrac{1}{p}}}dx\\ \\ &=&p\Big[\cfrac{x^{\scriptsize{\cfrac{1}{p}}+\normalsize{1}}}{\scriptsize{\cfrac{1}{p}}+\normalsize{1} } \Big]_{e^{-p}}^1\\ \\ &=&\cfrac{p^2}{p+1}\big( 1 - e^{ -p( \scriptsize{\dfrac{1}{p}}+\normalsize{1} ) } \big)\\ \\ &=&\cfrac{p^2}{p+1}\big( 1 - e^{-1-p } \big)\\ \end{eqnarray*}
$\quad 曲線 \ C_2\ と \ x\ 軸との交点は \ \ y=\log x + q =0 \quad より \quad x=e^{-q}=e^{-p}$
\begin{eqnarray*} S_2 &=&\int_{e^{-q}}^a (\log x + q)dx\\ \\ &=&\int_{e^{-p}}^1 (\log x + p)dx\\ \\ &=&\big[x\log x -x +px\big]_{e^{-p}}^1\\ \\ &=&\big[x\log x +(p-1)x\big]_{e^{-p}}^1\\ \\ &=&p-1-e^{-p}\log e^{-p} - (p-1)e^{-p}\\ \\ &=&p-1+e^{-p}\\ \end{eqnarray*}
(3)
\begin{eqnarray*} T &=&4S_2-3S_1\\ &=&4(p-1+e^{-p})-\cfrac{3p^2}{p+1}\big( 1 - e^{-1-p } \big)\\ \\ &=&4(p-1)-\cfrac{3p^2}{p+1} + \big(4+\cfrac{3p^2}{e(p+1)}\big)e^{-p }\\ \\ &=&\cfrac{p^2-4}{p+1} + \big(4+\cfrac{3p^2}{e(p+1)}\big)e^{-p }\\ \end{eqnarray*} $この第 \ 2\ 項目について \quad 2.5 < e < 3 \quad より \quad \cfrac{3}{e} > 1$
$両辺に \quad \cfrac{p^2}{p+1}e^{-p } > 0 \quad をかけて \quad \cfrac{3p^2}{e(p+1)}e^{-p } > \cfrac{p^2}{p+1}e^{-p } \quad だから$
\begin{eqnarray*} T &>&\cfrac{p^2-4}{p+1} + \big(4+\cfrac{p^2}{p+1}\big)e^{-p }\\ \\ &=&\cfrac{p^2-4}{p+1}+ \cfrac{(p+2)^2}{p+1}e^{-p }\\ \\ &=&\cfrac{p+2}{p+1}\big(p-2+(p+2)e^{-p}\big)\\ \end{eqnarray*}
$\quad f(p)=p-2+(p+2)e^{-p} \ \ (0 < p < 1)\ \ とおくと$
$\quad f'(p)=1+e^{-p}-(p+2)e^{-p}=1-(p+1)e^{-p}$
$\quad f''(p)=-e^{-p}+(p+1)e^{-p}=pe^{-p} > 0 \qquad よって \quad f'(p)\ は単調増加関数だから \quad f'(p) > f'(0)=1-e^0=0$
$\quad f'(p) > 0 \quad だから \quad f(p)\ は単調増加関数、よって \quad f(p) > f(0)=-2+2e^0=0 \qquad \therefore \ \ f(p) > 0$
$\quad \cfrac{p+2}{p+1} > 0 \quad だから \quad T > 0 \qquad よって \quad 4S_2> 3S_1$
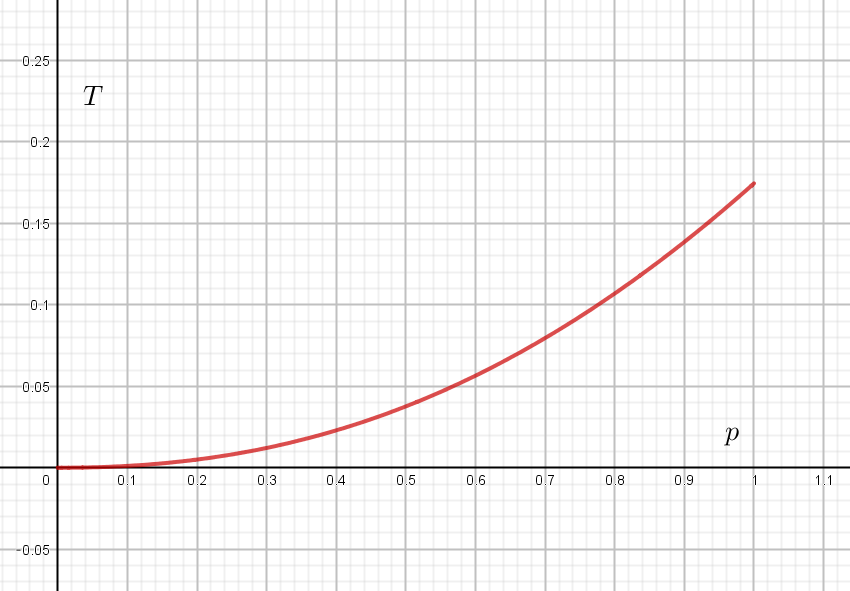
$\quad p \longrightarrow 0 \quad のとき \quad T \longrightarrow 0 \quad だから$
$等号を含めて \qquad \cfrac{S_2}{S_1} \geqq \cfrac{3}{4} $
$なお、参考までに$
$\quad T=4S_2-3S_1=\cfrac{p^2-4}{p+1} + \big(4+\cfrac{3p^2}{e(p+1)}\big)e^{-p }$
$のグラフは右図のとおりです。$
メインメニュー に戻る