筑波大学(理系) 2019年 問題6
$\ \ |z|^2+3=2(z+\overline{z}) を満たす複素数 \ z\ 全体の集合をAとする。ただし \ \overline{z}\ は \ z\ の共役複素数である。$
$(1)\ \ 集合Aを複素数平面上に図示せよ。$
$(2)\ \ Aの要素 \ z\ の偏角を\theta とする。ただし-\pi < \theta \leqq \pi \ \ とする。z\ がAを動くとき、\theta \ のとりうる値の$
$\quad \ 範囲を求めよ。$
$(3)\ \ z^{60}\ が正の実数となるAの要素 \ z\ の個数を求めよ。$
$(解説)$
$(1)\ \ よく見かける問題ですので、処理の方法はわかると思います。$
$(2)\ \ 図形的に考えるのが簡単です。別解として計算で求める方法も示します。$
$(3)\ \ (2)の条件をつかって求めますが、接する場合があることに注意しましょう。$
(1)
$|z|^2+3=2(z+\overline{z}) \quad より$
$z \overline{z} -2(z+\overline{z})+3=0$
$(z-2)(\overline{z} -2)=1$
$|z-2|^2=1$
$\therefore |z-2|=1$
$これは中心(2,0)、半径1の円を表す。図は下の図の赤い円です。$
(2)

$右図で直線 \ OP,\ OQは原点Oから引いた円の接線である。$
$\theta \ のとりうる値の範囲は、\angle QOP\ \ である。$
$\triangle OCP \ は \ OC=2,\ CP=1\ \ の直角三角形だから \angle COP=\cfrac{\pi}{6}$
$よって、\theta \ のとりうる値の範囲は\quad -\cfrac{\pi}{6} \leqq \theta \leqq \cfrac{\pi}{6}$
$(別解)$
$z=r(\cos \theta +i\sin \theta) \quad とおき、(1)より得られた \ \ |z-2|=1 \ \ に代入して$
$|r\cos \theta -2+ir\sin \theta |=1$
$(r\cos \theta -2)^2+(r\sin \theta)^2=1$
$r^2-4r\cos \theta +3=0$
$rの2次方程式とみて、これが正の解をもつ条件は$
(i)$\ \ 実数解をもつ$
$\quad \cfrac{D}{4}=(2\cos \theta )^2-3 \geqq 0$
(ii)$\ \ 解の積が3で正であることから和が正$
$\quad \cos \theta >0$
(i),(ii)$より \cos \theta \geqq \cfrac{\sqrt{3}}{2} \qquad これを満たす \ \theta \ の範囲は\quad -\cfrac{\pi}{6} \leqq \theta \leqq \cfrac{\pi}{6}$
(3)
$z=r(\cos \theta +i\sin \theta) \quad とおくと$
$z^{60}=r^{60}(\cos 60\ \theta +i\sin 60\ \theta) $
$z^{60}\ \ が正の実数となるのは \ \ \sin 60\ \theta =0 \ \ のときだから$
$ 60\ \theta =2n\pi \quad (nは整数) \quad \therefore \theta =\cfrac{n}{30}\pi $
$このとき \quad z^{60}=r^{60}\cos 2n\pi=r^{60} > 0 $
$(2)より\quad \theta \ のとりうる値の範囲は\quad -\cfrac{\pi}{6} \leqq \theta \leqq \cfrac{\pi}{6}\ \ だから$
$-\cfrac{\pi}{6} \leqq \cfrac{n}{30}\pi \leqq \cfrac{\pi}{6} \qquad \therefore -5 \leqq n \leqq 5$
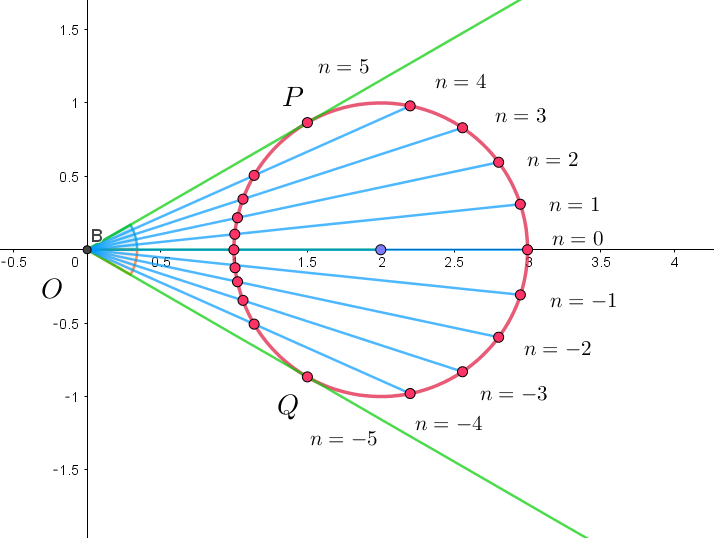
$これを満たす \ z\ は右図の赤い点で、n=\pm 5 \ \ は円に接することに$
$注意して全部で \ 20\ 個ある。$
メインメニュー に戻る