MY MATH NOTE

ベクトルの等式と面積比

$定理$
$\triangle ABC と点Pについて \ \ \triangle PBC : \triangle PCA : \triangle PAB =a:b:c \ \ とする。$
$(1)\ \ 点Pが\triangle ABC の内部にあるとき \qquad a\vec{PA}+b\vec{PB}+c\vec{PC}=\vec{0}$
$(2)\ \ 点Pが辺BCに関して点Aの反対側の\triangle ABC の外部にあるとき \qquad 　-a\vec{PA}+b\vec{PB}+c\vec{PC}=\vec{0}$

　
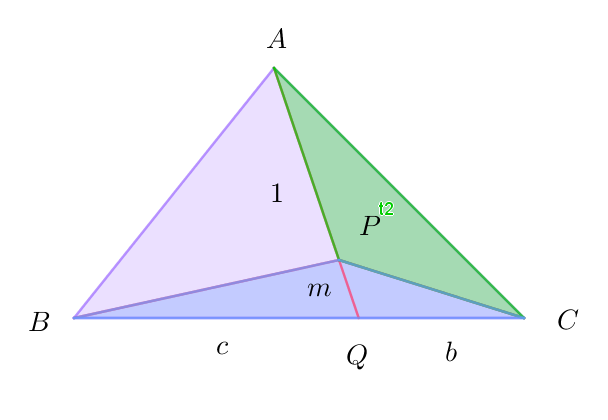
$線分APの延長と辺BCとの交点をQとする。$
$\triangle PCA : \triangle PAB =b:c \ \ より \ \ 　BQ:QC=c:b \ \ だから$

$\vec{AQ}=\cfrac{b\vec{AB}+c\vec{AC}}{b+c}$

$(b+c)\vec{AQ}=b\vec{AB}+c\vec{AC} \hspace{15em}①$

$AP:PQ=1:m \quad とおくと$
$\quad \triangle PCA : \triangle PCQ =1:m \ \ より \ \ 　\triangle PCQ =m \triangle PCA $
$\quad \triangle PAB : \triangle PBQ =1:m \ \ より \ \ 　\triangle PBQ =m \triangle PAB $
$\triangle PCQ + \triangle PBQ = \triangle PBC \quad より \quad m(\triangle PCA + \triangle PAB)= \triangle PBC $
$m(bk+ck)=ak \qquad \therefore m=\cfrac{a}{b+c}$

$したがって \quad \vec{AP}=\cfrac{1}{1+m}\vec{AQ}=\cfrac{1}{1+\cfrac{a}{b+c}}\vec{AQ}=\cfrac{b+c}{a+b+c}\vec{AQ}$
$\vec{AQ}=\cfrac{a+b+c}{b+c}\vec{AP}$

$①に代入して \qquad (a+b+c)\vec{AP}=b\vec{AB}+c\vec{AC}$

$点Pを始点とするベクトルになおすと$

$-(a+b+c)\vec{PA}=b(\vec{PB}-\vec{PA})+c(\vec{PC}-\vec{PA})$

$\quad \therefore \ \ a\vec{PA}+b\vec{PB}+c\vec{PC}=\vec{0}$


$(2)\ \ 点Pが辺BCに関して点Aの反対側の\triangle ABC の外部にある場合$

　
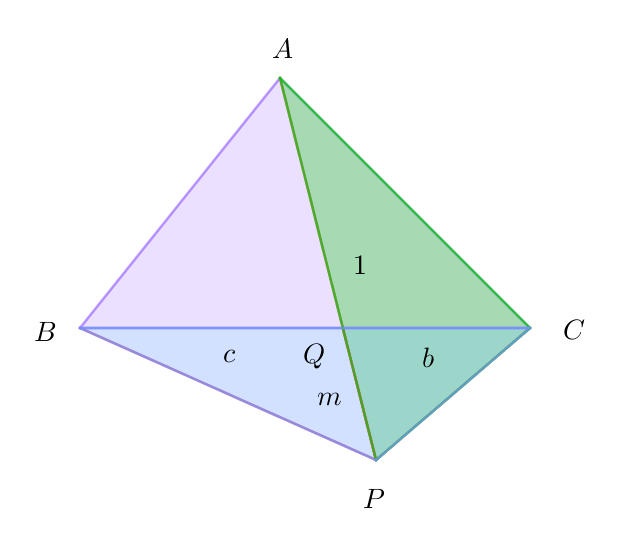
$線分APと辺BCとの交点をQとする。$
$\triangle PCA : \triangle PAB =b:c \ \ より \ \ 　BQ:QC=c:b \ \ だから$

$\vec{AQ}=\cfrac{b\vec{AB}+c\vec{AC}}{b+c}$

$(b+c)\vec{AQ}=b\vec{AB}+c\vec{AC} \hspace{15em}②$

$AP:QP=1:m \quad とおくと$
$\triangle PCA : \triangle PCQ =1:m \ \ より \ \ 　\triangle PCQ =m \triangle PCA $
$\triangle PAB : \triangle PBQ =1:m \ \ より \ \ 　\triangle PBQ =m \triangle PAB $
$\triangle PCQ + \triangle PBQ = \triangle PBC \quad より \quad m(\triangle PCA + \triangle PAB)= \triangle PBC $
$m(bk+ck)=ak \qquad \therefore m=\cfrac{a}{b+c}$

$したがって \quad \therefore \vec{AP}=\cfrac{1}{1-m}\vec{AQ}=\cfrac{1}{1-\cfrac{a}{b+c}}\vec{AQ}=\cfrac{b+c}{b+c-a}\vec{AQ}$
$\vec{AQ}=\cfrac{b+c-a}{b+c}\vec{AP}$

$②に代入して$
$(b+c-a)\vec{AP}=b\vec{AB}+c\vec{AC}$

$点Pを始点とするベクトルになおすと$

$-(b+c-a)\vec{PA}=b(\vec{PB}-\vec{PA})+c(\vec{PC}-\vec{PA})$

$\quad \therefore -a\vec{PA}+b\vec{PB}+c\vec{PC}=\vec{0}$


$なお$

$点Pが辺ACに関して点Bの反対側の\triangle ABC の外部にあるときは$

$\qquad a\vec{PA}-b\vec{PB}+c\vec{PC}=\vec{0}$

$点Pが辺ABに関して点Cの反対側の\triangle ABC の外部にあるときは$

$\qquad a\vec{PA}+b\vec{PB}-c\vec{PC}=\vec{0}$

$となることは同様にして示すことができる。$


$例題1$

　
$\triangle ABC と点Pについて \quad 3\vec{PA}+2\vec{PB}+\vec{PC}=\vec{0}$
$のとき、定理(1)が成りたつことを確認しましょう。$

$点Aを始点とするベクトルで表すと$
$-3\vec{AP}+2(\vec{AB}-\vec{AP})+(\vec{AC}-\vec{AP})=\vec{0}$

$\vec{AP}=\cfrac{1}{6}(2\vec{AB}+\vec{AC})=\cfrac{1}{2} \cdot \cfrac{2\vec{AB}+\vec{AC}}{3}$

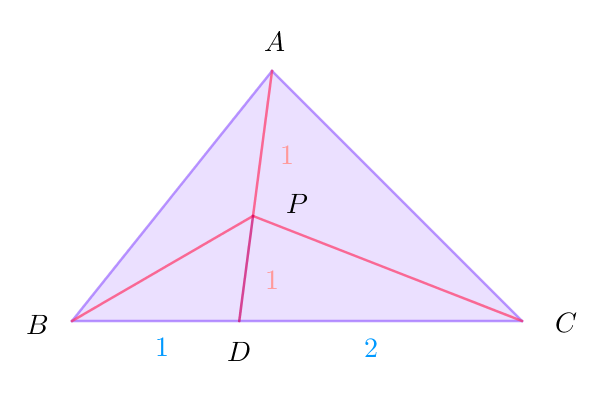
$\quad \vec{AD}=\cfrac{2\vec{AB}+\vec{AC}}{3} \quad とおくと \quad 点Dは辺BCを \ 1:2\ に内分する点で$

$\vec{AP}=\cfrac{1}{2}\vec{AD} \ \ より \ \ 点Pは線分ADの中点である。よって点Pは\triangle ABCの内部にある。$

$\quad \triangle PBD=S \quad とおくと\quad \triangle PCD=2S,\quad \triangle PAB=S,\quad \triangle PCA=2S \ \ だから$

$\triangle PBC : \triangle PCA : \triangle PAB =3S:2S:S=3:2:1$

$となって、確かに \quad \vec{PA},\vec{PB},\vec{PC}\ \ の係数に一致する。$


$例題2$

　
$\triangle ABC と点Pについて \quad 3\vec{PA}-2\vec{PB}+\vec{PC}=\vec{0}$
$のとき、定理(2)が成りたつことを確認しましょう。$

$点Bを始点とするベクトルで表すと$
$3(\vec{BA}-\vec{BP})+2\vec{BP}+(\vec{BC}-\vec{BP})=\vec{0}$

$\vec{BP}=\cfrac{1}{2}(3\vec{BA}+\vec{BC})=2 \cdot \cfrac{3\vec{BA}+\vec{BC}}{4}$

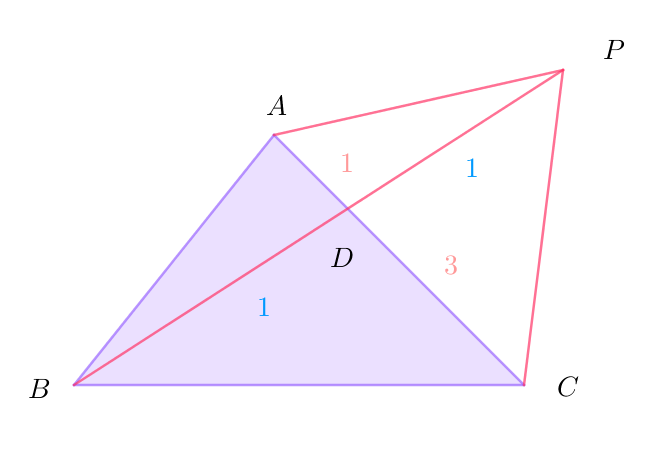
$\quad \vec{BD}=\cfrac{3\vec{BA}+\vec{BC}}{4} \quad とおくと \quad 点Dは辺ACを \ 1:3\ に内分する点で$

$\vec{BP}=2\vec{BD} \quad より \quad BD=DP$

$よって点Pは\triangle ABCの辺ACに関して点Bと反対側の外部にある。$

$\triangle PAD=S \quad とおくと \quad \triangle PCD=3S,\quad \triangle BAD=S,\quad \triangle BCD=3S \quad だから$

$\quad \triangle PBC : \triangle PCA : \triangle PAB =6S:4S:2S=3:2:1$

$となって、確かに \quad \vec{PA},\vec{PB},\vec{PC}\ \ の係数に一致する。$

ページの先頭へ↑