東京大学(理系) 2021年 問題5
$\alpha \ を正の実数とする。0 \leqq \theta \leqq \pi \ \ における \ \theta \ の関数 \ f(\theta) \ を、座標平面上の \ 2\ 点 \ A\ (-\alpha ,\ -3),\ P(\theta + \sin \theta,\ \cos \theta)$
$間の距離 \ AP\ の \ 2\ 乗として定める。$
$(1)\ 0 < \theta < \pi \ \ の範囲に \ f'(\theta)=0 \ となる \ \theta \ がただ \ 1\ つ存在することを示せ。$
$(2)\ 以下が成り立つような \ \alpha \ の範囲を求めよ。$
$\qquad 0 \leqq \theta \leqq \pi \ \ における \ \theta \ の関数 \ f(\theta) \ は、区間 \ \ 0 < \theta < \cfrac{\pi}{2} \ \ のある点において最大になる。$
$(解説)$
$(1)\ \ f''(\theta)\ の増減を調べればよいのですが、そのために \ f'''(\theta)\ の増減を調べる必要があります。$
$\qquad 具体的な \ \theta \ の値を求める必要はありません。$
$(2)\ \ f'(\theta)\ の増減を調べます。$
(1)
$f(\theta)=AP^2=(\theta + \sin \theta +\alpha)^2+(\cos \theta +3)^2$
$f'(\theta)=2(\theta +\theta \sin \theta +\alpha)(1+\cos \theta)+2(\cos \theta +3)(-\sin \theta)=2(\theta + \theta \cos \theta -2\sin \theta + \alpha \cos \theta +\alpha)$
$f''(\theta)=2(1+\cos \theta - \theta \sin \theta -2\cos \theta - \alpha \sin \theta )=2(1-\cos \theta - \theta \sin \theta - \alpha \sin \theta )$
$f'''(\theta)=2(\sin \theta -\sin \theta - \theta \cos \theta -\alpha \cos \theta )=-2(\theta + \alpha) \cos \theta $
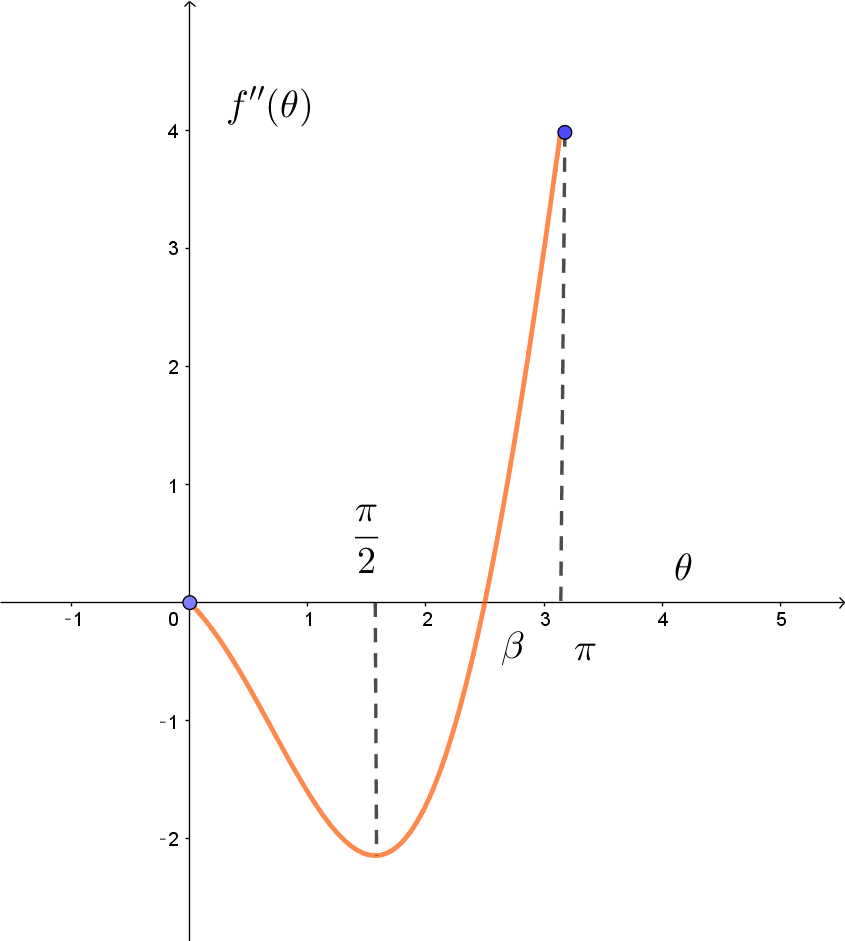
$f''(\theta) \ \ の増減表は$
\[
\begin{array}{c||c|c|c|c|c}
\hline
\theta & 0 & \cdots & \cfrac{\pi}{2} & \cdots & \pi \\
\hline
f'''(\theta )& & - & 0 & + & \\
\hline
f''(\theta) & 0 & \searrow & 極小 & \nearrow & 4 \\
\hline
\end{array}
\]
$f''(0)=0,\qquad \theta=\cfrac{\pi}{2} \ \ で極小だから 明らかに \ \ f''(\cfrac{\pi}{2}) <0$
$f''(\pi) > 0 \ \ だから中間値の定理より \ \ f''(\beta)=0 \ となる \ \beta \ が \ \ (\cfrac{\pi}{2} , \ \pi)\ に存在する。$
$しかもこの区間で \ f''(\theta) \ は単調増加だからただ \ 1\ つである。$
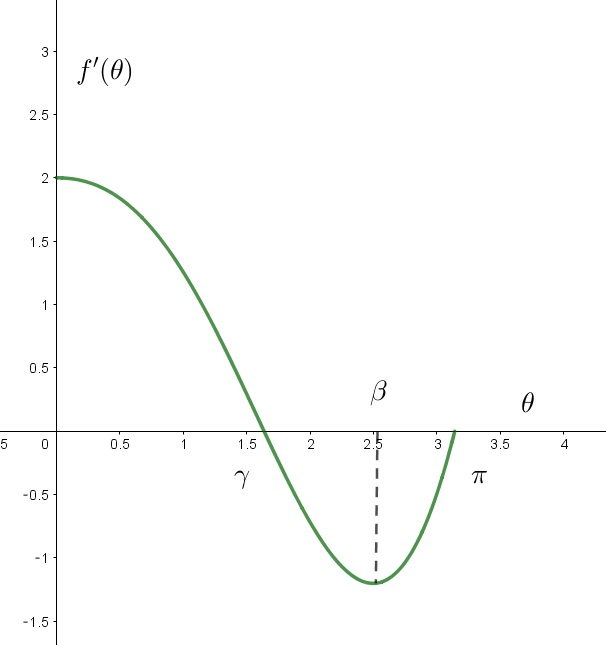
$f''(\theta) の増減表(グラフ)をつかって、f'(\theta)\ の増減表は$
\[
\begin{array}{c||c|c|c|c|c}
\hline
\theta & 0 & \cdots & \beta & \cdots & \pi \\
\hline
f''(\theta )& & - & 0 & + & \\
\hline
f'(\theta) & 4\alpha & \searrow & 極小 & \nearrow & 0 \\
\hline
\end{array}
\]
$f'(0)=4\alpha ,\quad \theta=\beta \ \ で極小となり \ \ f'(\pi)=0 \ \ だから \ \ f'(\beta) <0$
$f'(0) > 0 \ \ だから中間値の定理より \ \ f'(\gamma)=0 \ となる \ \gamma \ が \ (0 , \ \beta )\ に存在する。$
$しかもこの区間で \ f'(\theta)\ は単調減少だからただ \ 1\ つである。$
(2)
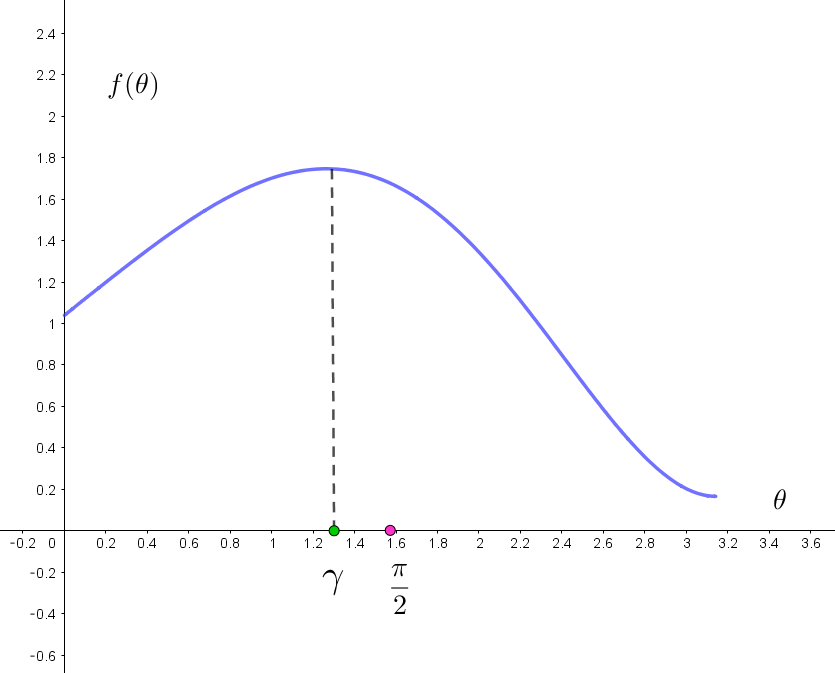
$f'(\theta) の増減表(グラフ)をつかって、f(\theta)\ の増減表は$
\[
\begin{array}{c||c|c|c|c|c}
\hline
\theta & 0 & \cdots & \gamma & \cdots & \pi \\
\hline
f'(\theta )& & + & 0 & - & \\
\hline
f(\theta) & & \nearrow & 極大 & \searrow & 0 \\
\hline
\end{array}
\]
$\theta=\gamma \ \ で極大となるが、0 < \gamma < \cfrac{\pi}{2} \ \ である条件は \ \ f'(\cfrac{\pi}{2})< 0$
$f'(\cfrac{\pi}{2})=2(\cfrac{\pi}{2} -2 +\alpha ) =\pi -4 +2\alpha $
$よって \quad \pi -4 +2\alpha < 0 \quad \therefore \ \ \alpha < 2-\cfrac{\pi}{2} \qquad \alpha > 0 \quad だから \quad 0 < \alpha < 2-\cfrac{\pi}{2}$
メインメニュー に戻る