東京大学(理系) 2021年 問題3
$関数 \ f(x)=\cfrac{x}{x^2+3}\ \ に対して \ \ y=f(x)\ のグラフを \ C\ とする。点A\ (1,\ f(1))\ における \ C\ の接線を$
$l:y=g(x)\ とする。$
$(1)\ C\ と \ l\ の共有点で \ A\ と異なるものがただ \ 1\ つ存在することを示し、その点の \ x\ 座標を求めよ。$
$(2)\ (1)で求めた共有点のx座標を \ \alpha \ とする。$
\[定積分 \quad \int _{\alpha}^1\{f(x)-g(x)\}^2 dx \quad を計算せよ。\]
$(解説)$
$(1)\ \ 接点のx座標で、重解をもちます。$
$(2)\ \ 平方を展開して、置換積分で求めます。$
(1)
$y=f(x)\ は奇関数だからグラフは原点に関して対称、$
$したがって \ \ x \geqq 0 \ \ を調べればよい。$
$f'(x)=-\cfrac{x^2-3}{(x^2+3)^2} \quad f'(x)=0 \quad より \quad x=\sqrt{3}$
$増減表$
\[
\begin{array}{c||c|c|c|c|c}
\hline
x& 0 & \cdots & \sqrt{3} & \cdots \\
\hline
f'(x)& & + & 0 & - & \\
\hline
f(x) & 0 & \nearrow & 極大 & \searrow & \\
\hline
\end{array}
\]
$x=\sqrt{3}\ \ で \ f(x)\ は極大となり、極大値は \ \ f(\sqrt{3})=\cfrac{\sqrt{3}}{6}$
$x \longrightarrow \infty \ \ のとき \ \ f(x) \longrightarrow 0 \ \ だから \ x\ 軸は漸近線である。$
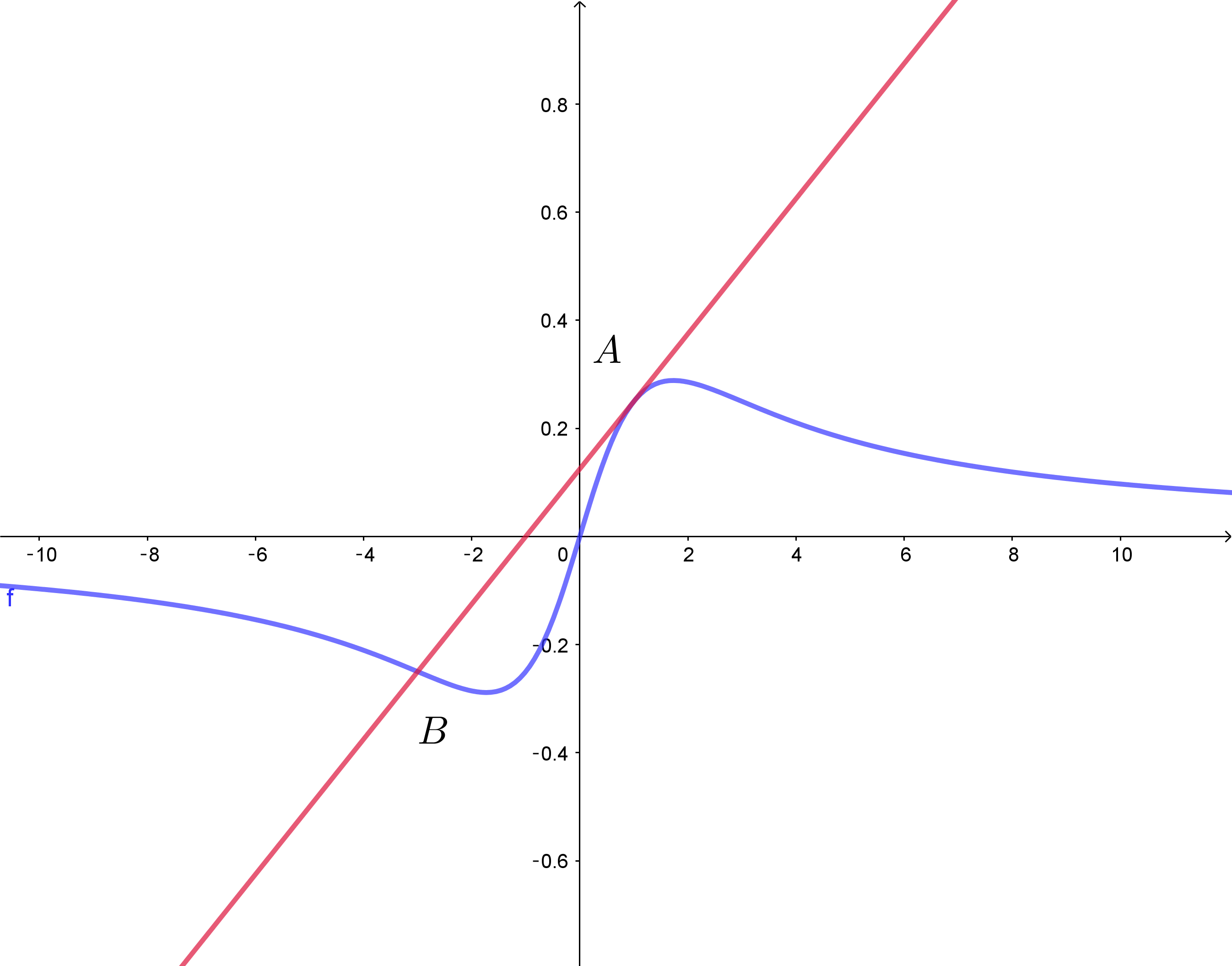
$y=f(x)\ のグラフは右のとおりである。$
$f'(1)=\cfrac{1}{8}\quad だから \quad 点 \ A(1,\ \cfrac{1}{4})\ における接線は \quad g(x)=\cfrac{1}{8}(x-1)+\cfrac{1}{4} \quad すなわち \quad l: y=\cfrac{1}{8}x+\cfrac{1}{8}$
$曲線 \ C\ と接線 \ l\ の共有点は \quad \cfrac{x}{x^2+3}=\cfrac{1}{8}x+\cfrac{1}{8} \qquad これを整理して$
$x^3+x^2-5x+3=0 \qquad x=1\ \ が重解であることに注意して因数分解すると \qquad (x-1)^2(x+3)=0$
$よって \quad A\ と異なる共有点は \quad x=-3\ \ ただ \ 1\ つである。$
(2)
\begin{eqnarray*} I &=&\int _{\alpha}^1\{f(x)-g(x)\}^2 dx \\ &=&\int _{-3}^1\big\{\cfrac{x}{x^2+3}-\cfrac{1}{8}(x+1)\big\}^2 dx \\ &=&\int _{-3}^1\big\{\cfrac{x^2}{(x^2+3)^2}-\cfrac{x(x+1)}{4(x^2+3)}+\cfrac{1}{64}(x+1)^2\big\}dx \\ \end{eqnarray*}$\quad 被積分項を順に \ \ I_1.\ \ I_2,\ \ I_3\ \ とおくと$
\[I_1=\int _{-3}^1\cfrac{x^2}{(x^2+3)^2}dx \quad は \] \[\quad x=\sqrt{3}\tan \theta \quad とおくと \quad dx=\sqrt{3}\cfrac{d\theta}{\cos ^2\theta} \qquad \begin{array}{c|c} x & \ -3 \ \ \rightarrow \ \ 1 \quad \\ \hline \theta & -\cfrac{\pi}{3} \rightarrow \cfrac{\pi}{6} \\ \end{array} \] \begin{eqnarray*} I_1 &=&\int \small{_{-\cfrac{\pi}{3}}^{\cfrac{\pi}{6}}}\normalsize{ 3\tan ^2 \theta \times \cfrac{1}{\{3(\tan ^2 \theta +1)\}^2} \times \cfrac{\sqrt{3}d\theta}{\cos ^2 \theta}}\\ &=&\int \small{_{-\cfrac{\pi}{3}}^{\cfrac{\pi}{6}}}\normalsize{ 3\tan ^2 \theta \times \cfrac{\cos ^4 \theta}{9} \times \cfrac{\sqrt{3}d\theta}{\cos ^2 \theta}}\\ &=&\int \small{_{-\cfrac{\pi}{3}}^{\cfrac{\pi}{6}}}\normalsize{ \cfrac{\sqrt{3}}{3}\tan ^2 \theta \times \cos ^2 \theta d\theta }\\ &=& \cfrac{\sqrt{3}}{3} \int \small{_{-\cfrac{\pi}{3}}^{\cfrac{\pi}{6}}}\normalsize{\sin ^2 \theta d\theta }\\ &=& \cfrac{\sqrt{3}}{6} \int \small{_{-\cfrac{\pi}{3}}^{\cfrac{\pi}{6}}}\normalsize{(1-\cos 2 \theta) d\theta }\\ &=& \cfrac{\sqrt{3}}{6} \big[\theta - \cfrac{\sin 2\theta}{2}\big] \small{_{-\cfrac{\pi}{3}}^{\cfrac{\pi}{6}}}\\ &=& \cfrac{\sqrt{3}}{6} \big(\cfrac{\pi}{2}-\cfrac{\sqrt{3}}{2}\big)\\ \end{eqnarray*}
\begin{eqnarray*} I_2 &=&\int _{-3}^1\cfrac{x(x+1)}{x^2+3}dx \\ &=&\int _{-3}^1\cfrac{x^2+3+x-3}{x^2+3}dx \\ &=&\int _{-3}^1\big(1+\cfrac{x}{x^2+3}-\cfrac{3}{x^2+3}\big)dx \\ &=&4+\big[\cfrac{1}{2}\log(x^2+3)\big]_{-3}^1-\int _{-3}^1\cfrac{3}{x^2+3}dx \\ &=&4+\cfrac{1}{2}(\log 4 - \log 12)-\int _{-3}^1\cfrac{3}{x^2+3}dx \\ &=&4-\cfrac{1}{2}\log 3-\int _{-3}^1\cfrac{3}{x^2+3}dx \\ \end{eqnarray*} \[\int _{-3}^1\cfrac{3}{x^2+3}dx \quad は \ \ I_1\ \ と同様に置換して\] \begin{eqnarray*} & &\int _{-3}^1\cfrac{3}{x^2+3}dx\\ &=&\int \small{_{-\cfrac{\pi}{3}}^{\cfrac{\pi}{6}}}\normalsize{ \cfrac{3}{3\tan ^2 \theta +3} \times \cfrac{\sqrt{3}d\theta}{\cos ^2 \theta}}\\ &=&\sqrt{3} \int \small{_{-\cfrac{\pi}{3}}^{\cfrac{\pi}{6}}}\normalsize{\cfrac{1}{1+\tan ^2 \theta}\times \cfrac{d\theta}{{\cos ^2 \theta}}}\\ &=&\sqrt{3} \int \small{_{-\cfrac{\pi}{3}}^{\cfrac{\pi}{6}}}\normalsize{d\theta }\\ &=&\cfrac{\sqrt{3}}{2}\pi\\ \end{eqnarray*} $\quad よって \quad I_2=4-\cfrac{1}{2}\log 3-\cfrac{\sqrt{3}}{2}\pi$
\begin{eqnarray*} I_3 &=&\int _{-3}^1\cfrac{1}{64}(x+1)^2dx \\ &=&\cfrac{1}{64} \times \cfrac{1}{3}\big[(x+1)^3\big]_{-3}^1\\ &=&\cfrac{1}{12}\\ \end{eqnarray*} $以上より$
\begin{eqnarray*} I &=&I_1-\cfrac{1}{4}I_2+I_3\\ \\ &=& \cfrac{\sqrt{3}}{6} \big(\cfrac{\pi}{2}-\cfrac{\sqrt{3}}{2}\big)-\cfrac{1}{4}\big(4-\cfrac{1}{2}\log 3-\cfrac{\sqrt{3}}{2}\pi\big)+\cfrac{1}{12}\\ \\ &=& \cfrac{5\sqrt{3}}{24}\pi +\cfrac{1}{8}\log 3-\cfrac{7}{6}\\ \end{eqnarray*}
メインメニュー に戻る