東京工業大学(理系) 2021年 問題2
$xy\ 平面上の楕円 \ \ E:\cfrac{x^2}{4}+y^2=1\ \ について、以下の問いに答えよ。$
$(1)\ \ a,\ b\ を実数とする。直線 \ l:y=ax+b \ \ と楕円 \ E\ が異なる \ 2\ 点を共有するための \ a,\ b\ の条件を求めよ。$
$(2)\ \ 実数 \ a,\ b,\ c\ に対して、直線 \ l:y=ax+b\ と直線 \ m:y=ax+c\ が、それぞれ楕円 \ E\ と異なる \ 2\ 点を共有$
$\quad しているとする。ただし、b > c \ とする。直線 \ l\ と楕円 \ E\ の \ 2\ つの共有点のうち \ x\ 座標の小さい方を \ P,$
$\quad 大きい方を \ Q\ とする。また、直線 \ m\ と楕円 \ E\ の \ 2\ つの共有点のうち \ x\ 座標の小さい方を \ S,大きい方を$
$\quad R\ とする。このとき、等式 \ \ \vec{PQ}=\vec{SR}\ \ が成り立つための \ a,\ b,\ c\ の条件を求めよ。$
$(3)\ \ 楕円 \ E\ 上の \ 4\ 点の組で、それらを \ 4\ 頂点とする四角形が正方形であるものをすべて求めよ。$
$(解説)$
$(1)\ \ 判別式が正であればよい。$
$(2)\ \ 直線 \ l\ と \ m\ は傾きが等しいので、PQ=SR\ \ であればよい。$
$(3)\ \ (2)で四角形 \ PQRS\ が平行四辺形である条件を求めてあるので、あとは \ PQ \perp PS\ と \ PQ=PS\ の条件を$
$\quad 求めればよい。$
(1)
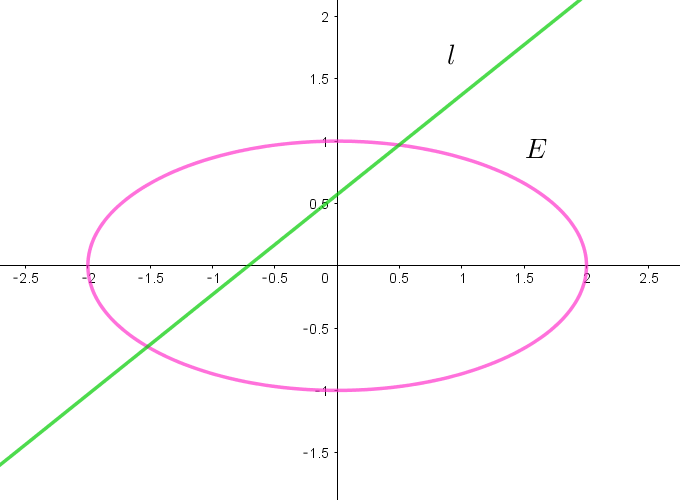
$E:x^2+4y^2=4 \quad に \quad l:y=ax+b \quad を代入して$
$\quad x^2+4(ax+b)^2=4$
$\quad (4a^2+1)x^2+8abx+4b^2-4=0 \hspace{10em}①$
$異なる2点を共有する条件は \quad \cfrac{D}{4} > 0 \quad だから$
$\quad \cfrac{D}{4}=(4ab)^2-(4a^2+1)(4b^2-4) > 0$
$これを整理して \qquad 4a^2-b^2+1 > 0$
(2)
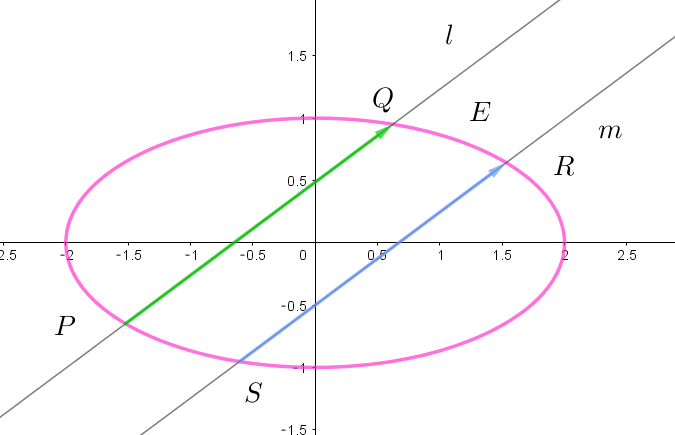
$直線 \ l\ と \ m\ は傾きが等しいので、PQ=SR\ \ であればよい。$
$P(x_1,\ y_1),\ \ Q(x_2,\ y_2),\ \ S(x_3,\ y_3)\ \ とおくと、x_1,\ \ x_2\ \ は①の解で \ \ x_1 < x_2 \quad だから$
$\quad x_1=\cfrac{-4ab-2\sqrt{4a^2-b^2+1}}{4a^2+1},\quad x_2=\cfrac{-4ab+2\sqrt{4a^2-b^2+1}}{4a^2+1}$
$よって \quad x_2-x_1=\cfrac{4\sqrt{4a^2-b^2+1}}{4a^2+1}$
\begin{eqnarray*}
PQ^2
&=&(x_2-x_1)^2+(y_2-y_1)^2\\
\\
&=&(x_2-x_1)^2+\{(ax_2+b)-(ax_1+b)\}^2\\
\\
&=&(x_2-x_1)^2+a^2(x_2-x_1)^2\\
\\
&=&(a^2+1)(x_2-x_1)^2\\
\\
&=&(a^2+1)\cfrac{16(4a^2-b^2+1)}{(4a^2+1)^2}\\
\\
&=&\cfrac{16(a^2+1)}{(4a^2+1)^2}(4a^2-b^2+1)\\
\end{eqnarray*}
$E:x^2+4y^2=4 \ と \ m:y=ax+c \ の交点の座標は、E:x^2+4y^2=4 \ と \ l:y=ax+b\ の交点の座標で、$
$b\ と \ c\ を入れ替えればよいから、E \ と \ m\ が異なる2点を共有する条件は \qquad 4a^2-c^2+1 > 0\ \ で$
$\qquad SR^2=\cfrac{16(a^2+1)}{(4a^2+1)^2}(4a^2-c^2+1)$
$\quad PQ=SR \quad より \quad b^2=c^2 \qquad b > c \quad だから \quad c=-b \quad ただし \quad b > 0$
$よって求める条件は \qquad 4a^2-b^2+1 > 0,\quad c=-b,\quad b > 0 $
(3)
$S(x_3,\ y_3)\ は \ P(x_1,\ y_1)\ で \ b\ を \ c\ と置き換えればよいが、さらに(2)より \ c=-b \ であるから$
$\quad x_1=\cfrac{-4ab-2\sqrt{4a^2-b^2+1}}{4a^2+1}$
$\quad y_1=ax_1+b=\cfrac{-4a^2b-2a\sqrt{4a^2-b^2+1}}{4a^2+1}+b=\cfrac{b-2a\sqrt{4a^2-b^2+1}}{4a^2+1}$
$より$
$\quad x_3=\cfrac{4ab-2\sqrt{4a^2-b^2+1}}{4a^2+1},\qquad y_3=\cfrac{-b-2a\sqrt{4a^2-b^2+1}}{4a^2+1}$
$四角形 \ PQRS\ が正方形となる条件は(2)の条件(平行四辺形)に加えて$
(i)$\ \ PQ \perp PS $
$\qquad (PQの傾き) \times (PSの傾き)=-1 \quad だから \quad a \times \cfrac{y_3-y_1}{x_3-x_1}=-1$
$\qquad a(y_3-y_1)=-(x_3-x_1)$
$\qquad a\big(\cfrac{-b-2a\sqrt{4a^2-b^2+1}}{4a^2+1}-\cfrac{b-2a\sqrt{4a^2-b^2+1}}{4a^2+1}\big)=-\big(\cfrac{4ab-2\sqrt{4a^2-b^2+1}}{4a^2+1}-\cfrac{-4ab-2\sqrt{4a^2-b^2+1}}{4a^2+1}\big)$
$\qquad -\cfrac{2ab}{4a^2+1}=-\cfrac{8ab}{4a^2+1}$
$\qquad \therefore \ \ ab=0 \qquad b > 0 \quad だから \quad a=0$
$\quad このとき$
$\qquad x_1=-2\sqrt{1-b^2},\quad y_1=b,\qquad x_2=2\sqrt{1-b^2},\quad y_2=b,\qquad x_3=-2\sqrt{1-b^2},\quad y_3=-b$
(ii)$\ \ PQ =PS $
$\qquad 4\sqrt{1-b^2}=2b \qquad 4(1-b^2)=b^2 \qquad b^2=\cfrac{4}{5} \qquad b > 0 \quad だから \quad b=\cfrac{2}{\sqrt{5}}$
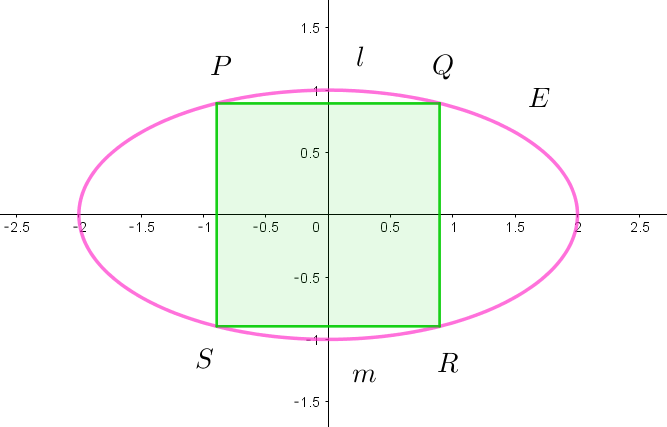
$したがって 四角形PQRSが正方形となるのは$
$\qquad P(-\cfrac{2}{\sqrt{5}},\ \cfrac{2}{\sqrt{5}}),\quad Q(\cfrac{2}{\sqrt{5}},\ \cfrac{2}{\sqrt{5}}),\quad
R(\cfrac{2}{\sqrt{5}},\ -\cfrac{2}{\sqrt{5}}),\quad S(-\cfrac{2}{\sqrt{5}},\ -\cfrac{2}{\sqrt{5}})$
$のときのみである。$
$(補充)$
$PQ \perp PS \ \ より \ \ a=0 \ \ が導かれたので、四角形 \ PQRS\ が長方形あるいは正方形となるのは$
$辺 \ PQ\ が \ x\ 軸に平行な場合のみであることがわかります。$
メインメニュー に戻る