東北大学(理系) 2021年 問題5
$z\ を複素数とする。複素数平面上の \ 3\ 点 \ O(0),\ A(z),\ B(z^2)\ について、以下の問いに答えよ。$
$(1)\ \ 3\ 点 \ O,\ A,\ B\ が同一直線上にあるための \ z\ の必要十分条件を求めよ。$
$(2)\ \ 3\ 点 \ O,\ A,\ B\ が二等辺三角形の頂点になるような \ z\ 全体を複素数平面上に図示せよ。$
$(3)\ \ 3\ 点 \ O,\ A,\ B\ が二等辺三角形の頂点であり、かつ \ z\ の偏角 \ \theta \ が \ \ 0 \leqq \theta \leqq \cfrac{\pi}{3}\ \ を満たすとき、$
$\qquad 三角形 \ OAB\ の面積の最大値とそのときの \ z\ の値を求めよ。$
$(解説)$
$(1)\ \ A,\ B\ の偏角が等しいか、\pi \ ずれているかのどちらかです。$
$(2)\ \ 3\ 通りのパターンがありますので、それぞれについて調べます。(1)の条件を忘れないこと。$
$(3)\ \ (2)のパターンごとに面積を求め、その最大値を求めます。$
$なお、今年度の「岡山大学(理系)の問題 \ 2」\ とほとんど一致してしています。全くの偶然でしょうが、$
$こんなこともあるのですね。$
(1)
$3\ 点 \ O,\ A,\ B\ が同一直線上にあるための条件は \quad \arg z^2=\arg z \quad あるいは \quad \arg z^2=\arg z +\pi$
$\arg z^2=2 \arg z \quad だから \quad \arg z=0 \quad あるいは \quad \arg z=\pi$
$したがって \quad z\ は実数である。$
$(別解)$
$\vec{OB}=k\vec{OA}\ \ (kは実数)\ とおけるから \quad z^2=kz$
$明らかに \quad z \ne 0 \quad だから \quad z=k$
(2)
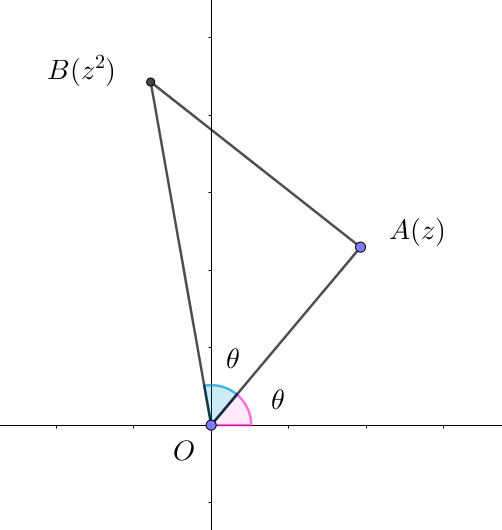
(i)$\ \ OA=OB \quad のとき$
$\quad OA=|z|,\quad OB=|z^2|=|z|^2 \quad だから \quad |z|=|z|^2$
$\quad |z| \ne 0 \quad より \quad |z|=1 \quad これは原点を中心とした半径 \ 1\ の円である。$
(ii)$\ \ OA=AB \quad のとき$
$\quad OA=|z|,\quad AB=|z^2-z|=|z(z-1)|=|z||z-1| \quad だから \quad |z|=|z||z-1|$
$\quad |z| \ne 0 \quad より \quad |z-1|=1 \quad これは \ C(1)\ を中心とした半径 \ 1\ の円である。$
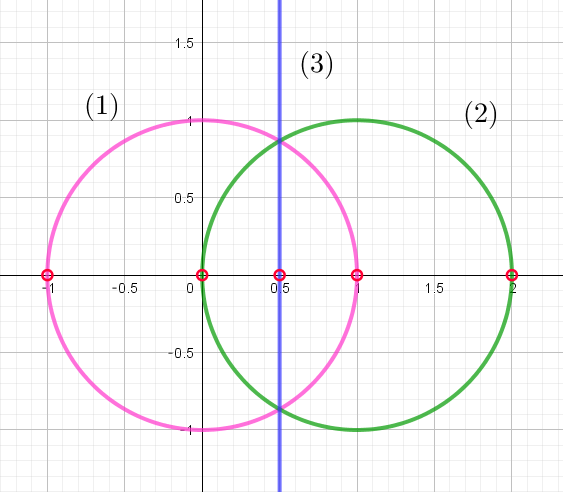
(iii)$\ \ OB=AB \quad のとき$
$\quad OB=|z|^2,\quad AB=|z||z-1| \quad より \quad |z|^2=|z||z-1|$
$\quad |z| \ne 0 \quad だから \quad |z|=|z-1| \quad これは \ A(z)\ と原点、$
$\quad A(z)\ と点 \ C(1)\ を結ぶ線分の距離が等しいことを示しているから$
$\quad 原点と点 \ C(1)\ を結ぶ線分の垂直二等分線である。$
(i),(ii),(iii)$ \ の各場合の \ z\ を図示したものが右のグラフである。$
$\quad ただし、(1)より \ z\ が実軸上にあるときは、3\ 点 \ O,\ A,\ B\ が同一直線上にあるため、それらの点を除く。$
(3)
$\quad \triangle OAB \ の面積を \ S\ とおく$
$\quad OB=OA^2,\quad \arg z=\theta \quad より \quad \arg z^2=2\theta \quad したがって \quad \angle AOB=\theta$
$\quad \therefore \ \ \triangle OAB=\cfrac{1}{2} OA\cdot OB \cdot \sin \angle AOB =\cfrac{1}{2}OA^3\sin \theta$
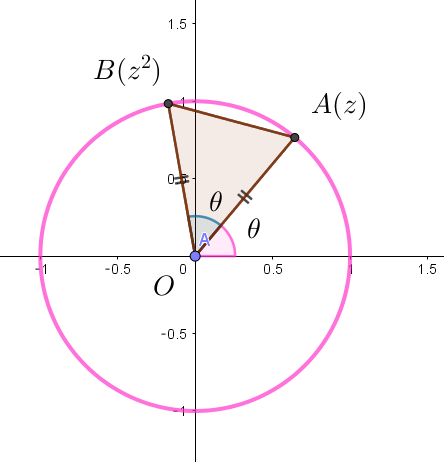
(i)$\ \ OA=OB \quad のとき$
$\quad |z|=1 \quad より \quad OA=1$
$\quad \triangle OAB=\cfrac{1}{2} \times 1^3 \times \sin \theta=\cfrac{1}{2}\sin \theta$
$\quad 0 \leqq \theta \leqq \cfrac{\pi}{3} \quad より \quad \theta =\cfrac{\pi}{3} \ \ のとき \ S\ は最大となり \quad 最大値 \ S_1\ は$
$\qquad S_1=\cfrac{1}{2}\sin \cfrac{\pi}{3}=\cfrac{\sqrt{3}}{4}$
$\quad このとき \quad z=\cos \cfrac{\pi}{3}+i\sin \cfrac{\pi}{3}=\cfrac{1}{2}+\cfrac{\sqrt{3}}{2}i$
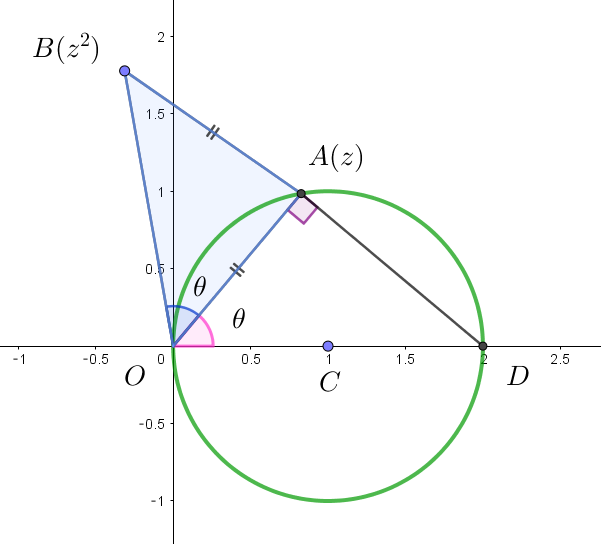
(ii)$\ \ OA=AB \quad のとき$
$\quad 点 \ D(2) \quad とおくと \quad \angle OAD \ は直径 \ OD\ の上にたつ円周角だから$
$\quad \angle OAD=90°\quad よって \quad OD=2 \quad より \quad OA=2\cos \theta $
\begin{eqnarray*}
\triangle OAB
&=&\cfrac{1}{2} \times (2\cos \theta)^3 \times \sin \theta\\
\\
&=&4\cos ^3\theta \sin \theta\\
\\
&=&2\cos ^2 \theta \times 2\sin \theta \cos \theta\\
\\
&=&(1+\cos 2\theta)\sin 2\theta\\
\\
&=&\sin 2\theta +\sin 2\theta \cos 2\theta\\
\\
&=&\sin 2\theta +\cfrac{1}{2}\sin 4\theta \\
\end{eqnarray*}
$\quad f(\theta)=\sin 2\theta +\cfrac{1}{2}\sin 4\theta \quad とおくと$
\begin{eqnarray*}
f'(\theta)
&=&2\cos 2\theta +2\cos 4\theta\\
\\
&=&2(\cos 2\theta +2\cos ^2 2\theta-1)\\
\\
&=&2(2\cos 2\theta -1)(\cos 2\theta +1)\\
\\
\end{eqnarray*}
$\quad 0 \leqq 2\theta \leqq \cfrac{2}{3}\pi \quad より \quad -\cfrac{1}{2} \leqq \cos 2\theta \leqq 1 \quad だから \quad \cos 2\theta +1 > 0$
$\quad f'(\theta)=0 \quad より \quad \cos 2\theta =\cfrac{1}{2} \qquad 2\theta=\cfrac{\pi}{3} \qquad \theta=\cfrac{\pi}{6}$
\[
\begin{array}{c||c|c|c|c|c}
\hline
\theta& 0 & \cdots & \dfrac{\pi}{6} & \cdots & \dfrac{\pi}{3}\\
\hline
f'(\theta)& & + & 0 & - & \\
\hline
f(\theta) & & \nearrow & 極大 & \searrow & \\
\hline
\end{array}
\]
$\quad \theta =\cfrac{\pi}{6}\ で \ f(\theta)\ すなわち \ S\ は極大かつ最大となり、最大値 \ S_2\ は$
$\qquad S_2=f(\cfrac{\pi}{6})=\sin \cfrac{\pi}{3} + \cfrac{1}{2}\sin \cfrac{2}{3}\pi=\cfrac{\sqrt{3}}{2}+\cfrac{1}{2} \times \cfrac{\sqrt{3}}{2}=\cfrac{3\sqrt{3}}{4}$
$\quad このとき \ \ z\ は$
$\quad x=|z|\cos \cfrac{\pi}{6}=2\cos ^2\cfrac{\pi}{6}=2 \times (\cfrac{\sqrt{3}}{2})^2=\cfrac{3}{2}$
$\quad y=|z|\sin \cfrac{\pi}{6}=2\cos \cfrac{\pi}{6}\sin \cfrac{\pi}{6}=\sin \cfrac{\pi}{3}=\cfrac{\sqrt{3}}{2} $
$\quad z=\cfrac{3}{2}+ \cfrac{\sqrt{3}}{2}i $
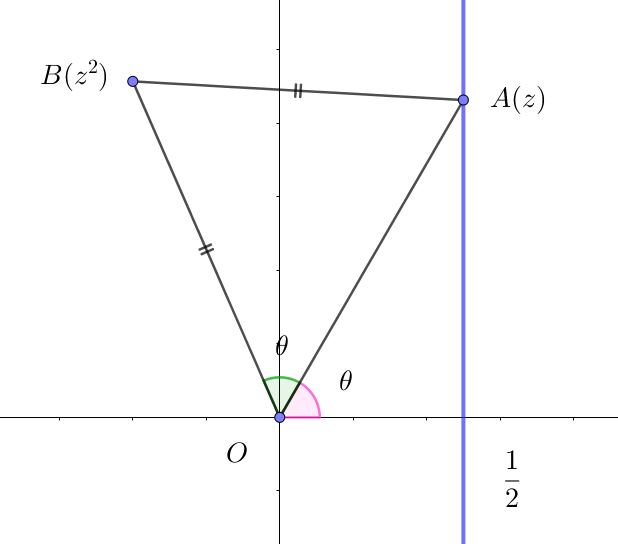
(iii)$\ \ OB=AB \quad のとき$
$\quad OA\cos \theta=\cfrac{1}{2} \quad より \quad OA=\cfrac{1}{2\cos \theta}$
\begin{eqnarray*}
\triangle OAB
&=&\cfrac{1}{2} \big(\cfrac{1}{2\cos \theta} \big)^3 \sin \theta\\
\\
&=&\cfrac{1}{16}\cdot \cfrac{\sin \theta}{\cos ^3 \theta}\\
\\
&=&\cfrac{1}{16} \cdot \cfrac{\sin \theta}{\cos \theta} \cdot \cfrac{1}{\cos ^2 \theta}\\
\\
&=&\cfrac{1}{16} \cdot \tan \theta (1+\tan ^2 \theta)\\
\\
\end{eqnarray*}
$\quad \tan \theta =x \quad とおくと \quad 0 \leqq \theta \leqq \cfrac{\pi}{3} \quad より \quad 0 \leqq x \leqq \sqrt{3}$
$\quad g(x)=x(1+x^2)=x+x^3 \quad は \quad g'(x)=1+3x^2 > 0 \quad だから \ g'(x)\ は単調増加$
$\quad よって \quad g(x)\ は \ \ x=\sqrt{3}\ \ のとき最大値 \quad g(\sqrt{3})=\sqrt{3}(1+3)=4\sqrt{3}\ \ をもつ。$
$\quad したがって \quad \triangle OAB \ の最大値 \ \ S_3 \ は \ \ S_3=\cfrac{1}{16} \times 4\sqrt{3}=\cfrac{\sqrt{3}}{4}$
$\quad このとき \quad \theta=\cfrac{\pi}{3} \quad だから \quad OA=\cfrac{1}{2\cos \dfrac{\pi}{3}}=1$
$\quad y=OA\sin \cfrac{\pi}{3}=\cfrac{\sqrt{3}}{2} \quad だから \quad z=\cfrac{1}{2}+ \cfrac{\sqrt{3}}{2}i $
(i),(ii),(iii)$より \quad \triangle OAB \ \ の面積の最大は \ $(ii)$\ のとき、すなわち \ \ OA=AB \ \ のときで$
$最大値は \quad \cfrac{3\sqrt{3}}{4} \quad このとき \quad z=\cfrac{3}{2}+ \cfrac{\sqrt{3}}{2}i $
メインメニュー に戻る