東北大学(理系) 2021年 問題4
$座標平面において、次の条件\ (*)\ を満たす直線 \ l\ を考える。$
$\qquad (*)\quad l\ の傾きは \ 1\ で、曲線 \ \ y=x^3-2x\ \ と異なる \ 3\ 点で交わる。$
$その交点を \ x\ 座標が小さなものから順に \ P,\ Q,\ R\ とし、さらに線分 \ PQ\ の中点を \ S\ とする。$
$(1)\ \ 点 \ R\ の座標を \ (a,\ a^3-2a)\ とするとき、点 \ S\ の座標を求めよ。$
$(2)\ \ 直線 \ l\ が条件 \ (*)\ を満たしながら動くとき、点 \ S\ の軌跡を求めよ。$
$(3)\ \ 直線 \ l\ が条件 \ (*)\ を満たしながら動くとき、線分 \ PS\ が動いてできる領域の面積を求めよ。$
$(解説)$
$(1)\ \ 点\ R\ の座標から点 \ P,\ Q\ の \ x\ 座標を満たす方程式が求められます。$
$(2)\ \ (1)より点 \ S\ の座標が \ a\ の式で求まれば、a\ を消去して軌跡が求まります。動ける範囲も求めます。$
$(3)\ \ (2)より点 \ S\ の軌跡が求まれば、点 \ P\ は与えられた曲線上を動くので領域がわかります。$
(1)
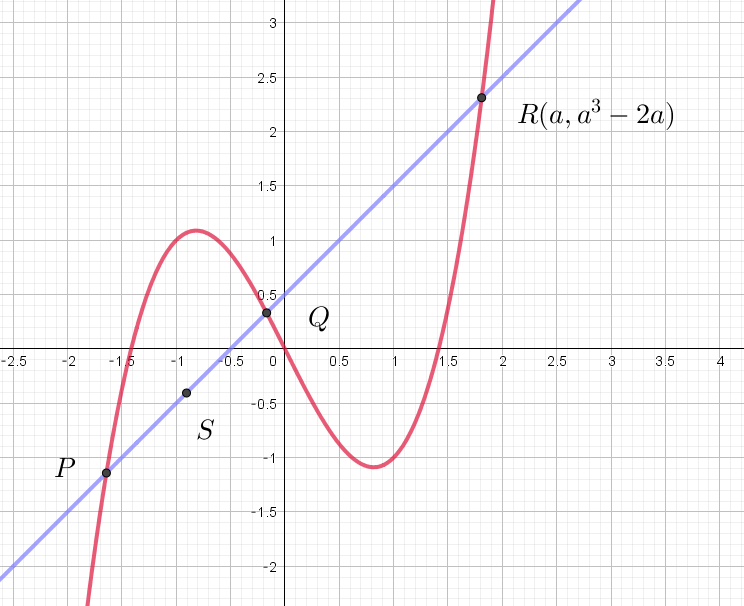
$y=x^3-2x \ \ は奇関数だからグラフは原点について対称。$
$y'=3x^2-2 \qquad y'=0 \quad より \quad x=\cfrac{\sqrt{6}}{3}$
\[
\begin{array}{c||c|c|c|c|c}
\hline
x& 0 & \cdots & \dfrac{\sqrt{6}}{3} & \cdots \\
\hline
y'& & - & 0 & + & \\
\hline
y& & \searrow & 極小 & \nearrow & \\
\hline
\end{array}
\]
$x=\cfrac{\sqrt{6}}{3}\ で \ y\ は極小となり、極小値は \ \ y=\cfrac{2\sqrt{6}}{9}-\cfrac{2\sqrt{6}}{3}=-\cfrac{4\sqrt{6}}{9}$
$対称性から \quad x=-\cfrac{\sqrt{6}}{3}\ で \ y\ は極大となり、極大値は \ \ y=\cfrac{4\sqrt{6}}{9}$
$l:y=x+b \quad とおくと 交点は$
$\quad x^3-2x=x+b \qquad x^3-3x-b=0$
$\quad x=a \ \ は解だから \quad a^3-3a-b=0 \qquad b=a^3-3a$
$よって交点の \ x\ 座標は \quad x^3-3x-a^3+3a=0 \qquad (x-a)(x^2+ax+a^2-3)=0 \ \ の解である。$
$P(\alpha,\ \alpha +b),\ \ Q(\beta,\ \beta+b),\ \ S(\gamma,\ \gamma+b)\ \ とおくと、\alpha,\ \beta \ は$
$\quad x^2+ax+a^2-3=0 \hspace{5em}①$
$の解である。$
$解と係数の関係より\quad \gamma =\cfrac{\alpha +\beta}{2}=-\cfrac{a}{2}$
$\quad \gamma +b=-\cfrac{a}{2}+a^3-3a=a^3-\cfrac{7}{2}a$
$したがって \quad S(-\cfrac{a}{2},\ a^3-\cfrac{7}{2}a)$
(2)
$(1)より \ \ S(-\cfrac{a}{2},\ a^3-\cfrac{7}{2}a) \quad だから \quad x=-\cfrac{a}{2},\quad y=a^3-\cfrac{7}{2}a \quad とおくと$
$a=-2x \quad を代入して \quad y=(-2x)^3-\cfrac{7}{2} \times (-2x)=-8x^3+7x$
$ただし、(1)の①式は異なる \ 2\ つの実数解 \ \alpha,\ \beta \ \ をもち、\alpha < a,\ \ \beta < a \ \ であるから$
$\quad \alpha - a < 0 , \quad \beta -a < 0 $
$よって条件は$
(i)$\ \ D=a^2-4(a^2-3) > 0 \quad より \quad a^2-4 < 0 \qquad -2 < a < 2$
(ii)$\ \ (\alpha -a)+(\beta -a) < 0 \quad より \quad \alpha +\beta <2a \qquad -a < 2a \qquad a > 0$
(iii)$\ \ (\alpha -a)(\beta -a) > 0 \quad より \quad \alpha \beta -a(\alpha +\beta)+a^2 >0 $
$\qquad \ \ (a^2-3)-a \times (-a) +a^2>0 \qquad a^2-1 > 0 \qquad a < -1 ,\ \ a >1 $
(i),(ii),(iii)$\ \ より\quad 1 < a < 2$
$a=-2x \quad だから \quad 1 < -2x < 2 \qquad -1 < x <-\cfrac{1}{2}$
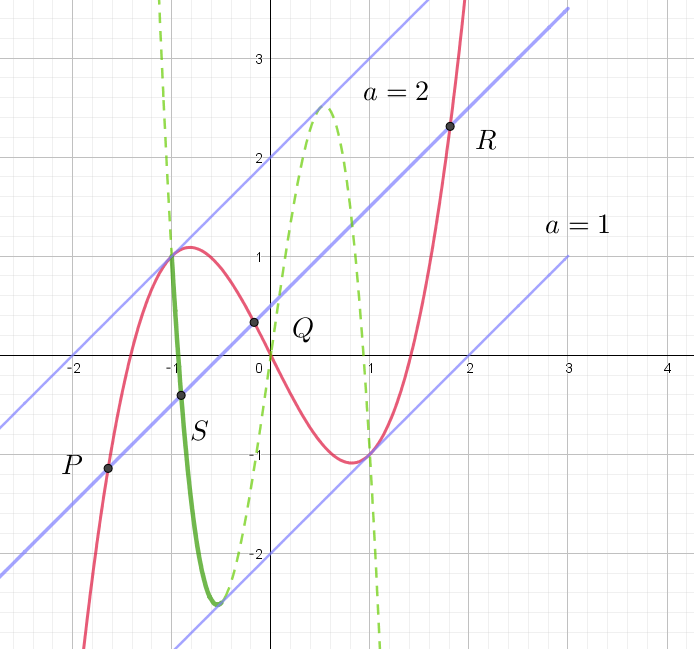
$したがって 点 \ S\ の軌跡は \quad y=-8x^3+7x \ \ (-1 < x <-\cfrac{1}{2})$
$グラフは右図のとおり$
$なお、a\ の値の範囲を求める別解として、次のような方法がある。$
$(1)の①式 \quad x^2+ax+a^2-3=0 \quad は異なる \ 2\ つの実数解 \alpha,\ \ \beta \ \ をもち、\alpha < a,\ \ \beta < a \ \ であるから$
(i)$\ \ D=a^2-4(a^2-3) >0 \quad より \quad -2 < a < 2$
(ii)$\ \ y=x^2+ax+a^2-3 \quad の軸について \quad -\cfrac{a}{2} < a \quad より \quad a>0$
(iii)$\ \ x=a \ \ のときの \ y\ の値について \quad a^2+a^2+a^2-3 >0 \quad より \quad a^2-1>0$
(3)
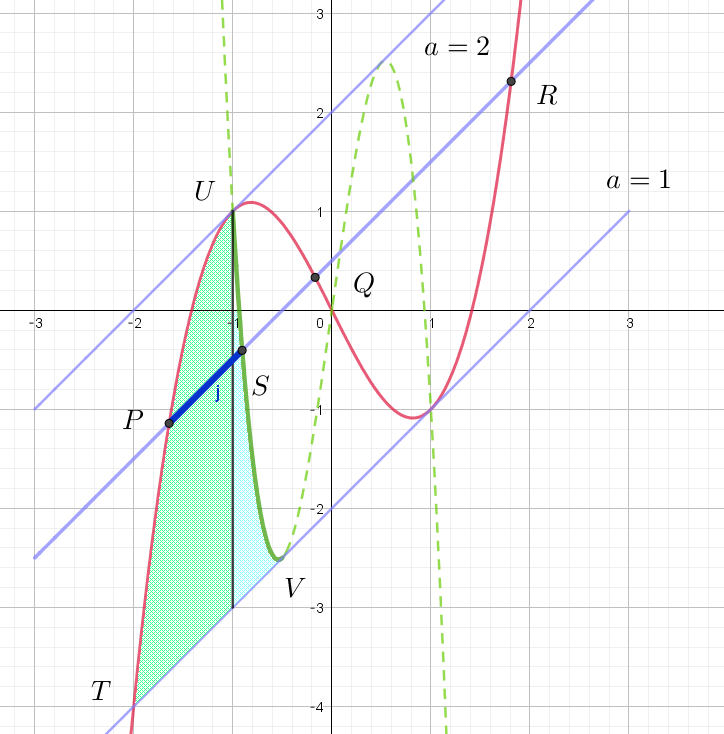
$点 \ P\ は曲線 \ \ y=x^3-2x \ \ 上にあるから、線分 \ PS\ が動いてできる領域は$
$右図のとおりである。$
$a=1\ \ のとき \ \ ①式 \quad x^2+x-2=0 \quad より \quad x=-2 \quad よって \quad T(-2,\ -4)$
$また \quad U(-1,\ 1),\quad V(-\cfrac{1}{2},\ -\cfrac{5}{2}) $
$この領域の面積を \ S\ とすると$
\begin{eqnarray*}
S
&=&\int_{-2}^{-1}\{(x^3-2x)-(x-2)\}dx+\int_{-1}^{-\scriptsize{\cfrac{1}{2}}}\{(-8x^3+7x)-(x-2)\}dx\\
\\
&=&\int_{-2}^{-1}(x^3-3x+2)dx+\int_{-1}^{-\scriptsize{\cfrac{1}{2}}}(-8x^3+6x+2)dx\\
\\
&=&\big[\cfrac{x^4}{4}-\cfrac{3}{2}x^2+2x\big]_{-2}^{-1}+\big[-2x^4+3x^2+2x\big]_{-1}^{-\scriptsize{\cfrac{1}{2}}}\\
\\
&=&\big(\cfrac{1}{4}-\cfrac{3}{2}-2\big)-(4-6-4)+\big(-\cfrac{1}{8}+\cfrac{3}{4}-1\big)-(-2+3-2)\\
\\
&=&\cfrac{27}{8}
\end{eqnarray*}
メインメニュー に戻る