東北大学(理系) 2021年 問題2
$a,\ b\ を \ \ 0 < a <1,\ \ 0 < b < 1 \ \ を満たす実数とする。平面上の三角形 \ ABC\ を考え、辺 \ AB\ を \ a\ :\ 1-a \ \ に$
$内分する点を \ P、辺 \ BC\ を \ b\ :\ 1-b\ に内分する点を \ Q、辺 \ CA\ の中点を \ R\ とし、三角形 \ ABC\ の面積を \ S、$
$三角形 \ PQR\ の面積を \ T\ とする。$
$\quad (1)\ \ \cfrac{T}{S}\ を \ a,\ b\ で表せ。$
$\quad (2)\ \ a,\ b\ が \ \ 0 < a < \cfrac{1}{2},\ \ 0 < b <\cfrac{1}{2}\ \ の範囲を動くとき、\cfrac{T}{S}\ \ がとりうる値の範囲を求めよ。$
$\quad (3)\ \ p,\ q\ を \ 3\ 以上の整数とし、a=\cfrac{1}{p},\ \ b=\cfrac{1}{q}\ \ とする。\cfrac{T}{S}\ の逆数 \ \ \cfrac{S}{T}\ が整数となりような \ p,\ q\ の組$
$\qquad (p,\ q)\ をすべて求めよ。$
$(解説)$
$(1)は中学校の図形の問題ですが、高さが等しい \ 2\ つの三角形の面積比は底辺の比になります。$
$(2)は \ a,\ b\ に関数関係はありませんので、a,\ b\ の範囲をつかって求めます。$
$(3)は(2)より \ \cfrac{T}{S}\ が求まりますので、(1)をつかって \ p,\ q\ の不定方程式を解きます。$
(1)
$\hspace{10em}$(i)$\hspace{15em}$(ii)$\hspace{16em}$(iii)
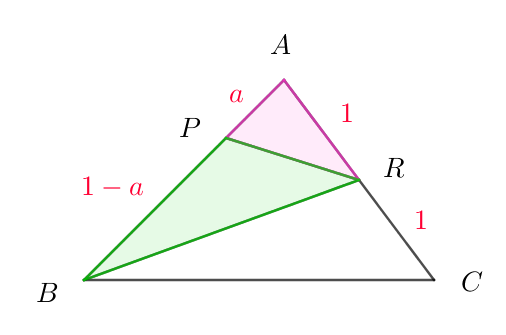
(i)$\ \ AR:RC=1:1 \quad より \quad \triangle ABR=\cfrac{1}{2}\triangle ABC=\cfrac{1}{2}S$
$\qquad \triangle APR=a\ \triangle ABR=\cfrac{a}{2}S$
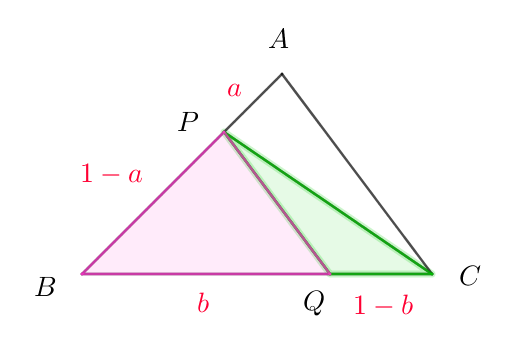
(ii)$\ \ AP:PB=a:1-a \quad より \quad \triangle BCP=(1-a)\triangle ABC=(1-a)S$
$\qquad \triangle BQP=b\ \triangle BCP=b(1-a)S$
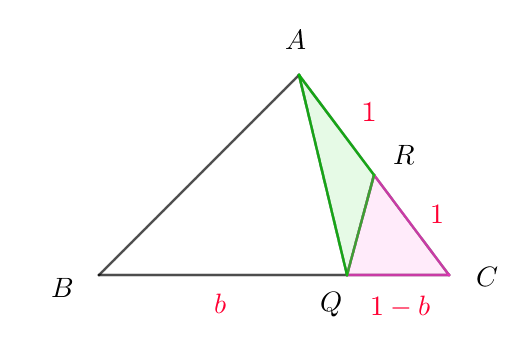
(iii)$\ \ BQ:QC=b:1-b \quad より \quad \triangle CAQ=(1-b)\triangle ABC=(1-b)S$
$\qquad \triangle CRQ=\cfrac{1}{2}\ \triangle CAQ=\cfrac{1}{2}(1-b)S$
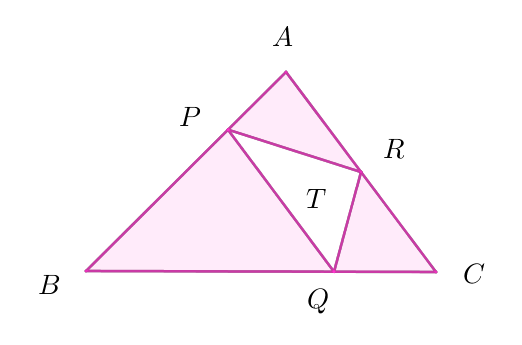
(i),(ii),(iii)$より$
\begin{eqnarray*}
T
&=&\triangle ABC-\triangle APR-\triangle BQP-\triangle CRQ\\
\\
&=&S-\cfrac{a}{2}S - b(1-a)S - \cfrac{1}{2}(1-b)S\\
\\
&=&(ab - \cfrac{1}{2}a - \cfrac{1}{2}b +\cfrac{1}{2})S\\
\end{eqnarray*}
$\quad \therefore \ \ \cfrac{T}{S}=ab - \cfrac{1}{2}a - \cfrac{1}{2}b +\cfrac{1}{2}$
(2)
(i)
$\qquad \cfrac{T}{S}=ab - \cfrac{1}{2}a - \cfrac{1}{2}b +\cfrac{1}{2}=(\cfrac{1}{2}-a)(\cfrac{1}{2}-b)+\cfrac{1}{4}$
$\qquad 0 < a < \cfrac{1}{2},\ \ 0 < b <\cfrac{1}{2} \quad だから \quad (\cfrac{1}{2}-a)(\cfrac{1}{2}-b) > 0$
$\quad よって \quad \cfrac{T}{S} > \cfrac{1}{4}$
(ii)
$\qquad \cfrac{T}{S}=a(b-\cfrac{1}{2})-\cfrac{1}{2}b +\cfrac{1}{2}$
$\qquad a > 0,\quad b-\cfrac{1}{2} < 0 \quad だから \quad a(b-\cfrac{1}{2})< 0 $
$\quad よって \quad \cfrac{T}{S} < \cfrac{1}{2}$
(i),(ii)$\ \ より \qquad \cfrac{1}{4} < \cfrac{T}{S} < \cfrac{1}{2}$
(3)
$\qquad \cfrac{1}{4} < \cfrac{T}{S} < \cfrac{1}{2} \quad より \quad 2 < \cfrac{S}{T} < 4$
$\qquad \cfrac{S}{T}\ \ は整数だから \quad \cfrac{S}{T}=3 \quad すなわち \quad \cfrac{T}{S}=\cfrac{1}{3}$
$\qquad ab - \cfrac{1}{2}a - \cfrac{1}{2}b +\cfrac{1}{2}=\cfrac{1}{3} \quad に \quad a=\cfrac{1}{p},\ \ b=\cfrac{1}{q}\ \ を代入して$
$\qquad \cfrac{1}{pq}-\cfrac{1}{2p}-\cfrac{1}{2q}+\cfrac{1}{6}=0$
$\qquad pq-3p-3q+6=0$
$\qquad (p-3)(q-3)=3$
$\quad p,\ q \ \ は \ 3\ 以上の整数だから$
$\quad $(i)$\ \ p-3=1,\quad q-3=3 \quad のとき \quad p=4,\quad q=6$
$\quad $(ii)$\ \ p-3=3,\quad q-3=1 \quad のとき \quad p=6,\quad q=4$
$\quad よって \quad (p,\ q)=(4,\ 6),\ \ (6,\ 4)$
メインメニュー に戻る