MY MATH NOTE

2次曲線の接線

　
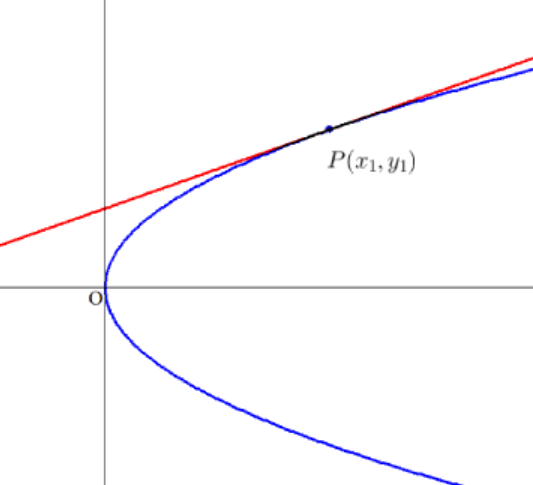
$(1)\ \ 放物線 \ \ y^2=4px$

$接線は明らかにx軸に平行でないから$

$\qquad x=m(y-y_1)+x_1 \hspace{10em}①$

$\quad とおけるので$

$\qquad y^2=4p\{m(y-y_1)+x_1\}$

$\qquad y^2-4pmy+4p(my_1-x_1)=0$

$\quad これが重解をもつから \quad \cfrac{D}{4}=(2pm)^2-4p(my_1-x_1)=0$

$\qquad y_1^2=4px_1 \quad を代入して　4p^2m^2-4pmy_1+y_1^2=0$

$\qquad (2pm-y_1)^2=0 \qquad m=\cfrac{y_1}{2p}$

$\quad なお \quad y=y_1\ \ が重解であるから、解と係数の関係より$

$\qquad y_1+y_1=4pm \quad \therefore m=\cfrac{y_1}{2p}\quad と簡単に求めることもできます。$

$\quad これを①に代入して　x= \cfrac{y_1}{2p}(y-y_1)+x_1$

$\qquad 2px=y_1y-y_1^2+2px_1$

$\qquad y_1^2=4px_1 \ \ を代入して \quad 　2px=y_1y-4px_1+2px_1$

$\qquad \therefore y_1y=2p(x+x_1) $

$\quad 同様にして \quad x^2=4py \ \ の接線は \qquad x_1x=2p(y+y_1)$

　
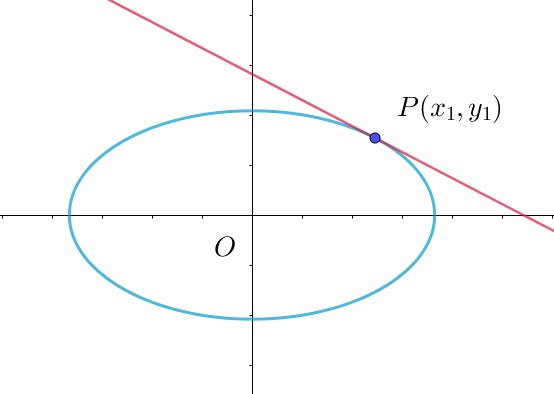
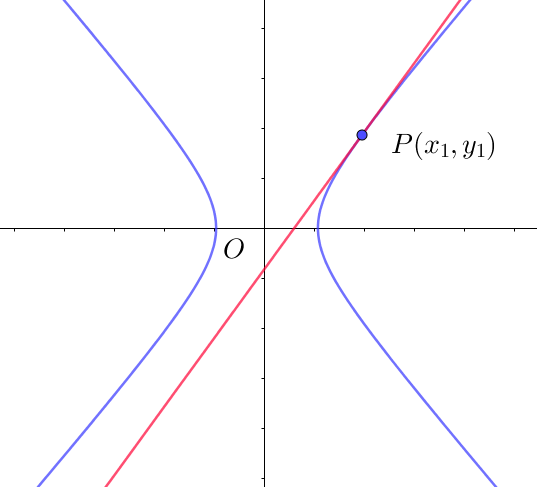
$(2)\ \ 楕円・双曲線 Ax^2+By^2=1$

(i)$\ \ y_1 = 0 \quad のとき$

$\qquad x_1=\pm \cfrac{1}{\sqrt{A}} \quad だから接線は \quad x=\pm \cfrac{1}{\sqrt{A}}$


(ii)$\ \ y_1 \ne 0 \quad のとき$

$\quad 接線を \quad y=m(x-x_1)+y_1 \hspace{10em}②$

$\quad とおくと$

　
$\qquad Ax^2+B\{mx-(mx_1-y_1)\}^2=1$

$\qquad (A+Bm^2)x^2-2Bm(mx_1-y_1)x+B(mx_1-y_1)^2-1=0$

$\quad x=x_1\ \ が重解であるから、解と係数の関係より$

$\qquad x_1+x_1=\cfrac{2Bm(mx_1-y_1)}{A+Bm^2}$

$\qquad x_1(A+Bm^2)=Bm(mx_1-y_1) \qquad Ax_1=-Bmy_1$

$\qquad \therefore m=-\cfrac{Ax_1}{By_1}$

$\quad これを②に代入して \quad 　y=-\cfrac{Ax_1}{By_1}(x-x_1)+y_1$

$\qquad Ax_1x+By_1y=Ax_1^2+By_1^2$

$\qquad P(x_1,y_1)\ \ は \ \ Ax^2+By^2=1 \quad 上の点だから \quad Ax_1^2+By_1^2=1$

$\quad よって \quad Ax_1x+By_1y=1$

$\quad これは \quad y_1=0 \quad のときも含んでいる。$

$\quad したがって接線は \qquad Ax_1x+By_1y=1$

$\quad とくに標準形 \quad \cfrac{x^2}{a^2} \pm \cfrac{y^2}{b^2}=1 \quad のときは \quad \cfrac{x_1x}{a^2} \pm \cfrac{y_1y}{b^2}=1 $


$2 \quad 傾きmの接線$

$(1)\ \ 放物線 \quad y^2=4px$

$\quad 接線を \quad y=mx+n \hspace{10em}①$

$\quad とおくと \qquad (mx+n)^2=4px$

$\qquad m^2x^2+2(mn-2p)x+n^2=0$

$\quad これが重解をもつから \quad \cfrac{D}{4}=(mn-2p)^2-m^2n^2=0 \qquad \therefore n=\cfrac{p}{m}$

$\quad よって　y=mx+\cfrac{p}{m}$

$\quad なお、接点は重解だから \quad x=-\cfrac{mn-2p}{m^2}=\cfrac{p}{m^2}$

$\qquad y=m \times \cfrac{p}{m^2}+\cfrac{p}{m}=\cfrac{2p}{m}$

$\quad よって \quad (\cfrac{p}{m^2},\cfrac{2p}{m})$

$\quad 放物線 \quad x^2=4py \quad の接線は \ x\ と \ y\ を入れ替えて \qquad 　x=my+\cfrac{p}{m}$

$\quad 接点は \ \ (\cfrac{2p}{m},\cfrac{p}{m^2})$


$(2)\ \ 楕円・双曲線 \quad Ax^2+By^2=1$

$\quad 接線を \quad y=mx+n \hspace{10em}②$

$\quad とおくと \qquad Ax^2+B(mx+n)^2=1$

$\qquad (A+Bm^2)x^2 +2Bmnx+Bn^2-1=0$

$\quad これが重解をもつから \qquad \cfrac{D}{4}=B^2m^2n^2-(A+Bm^2)(Bn^2-1)=0 \qquad -ABn^2+A+Bm^2=0$

$\qquad n^2=\cfrac{m^2}{A}+\cfrac{1}{B} \qquad n=\pm \sqrt{\cfrac{m^2}{A}+\cfrac{1}{B}}$

$\quad よって接線は \quad y=mx \pm \sqrt{\cfrac{m^2}{A}+\cfrac{1}{B}}$

$\quad とくに標準形 \quad \cfrac{x^2}{a^2} \pm \cfrac{y^2}{b^2}=1 \quad のときは \quad A=\cfrac{1}{a^2},B=\cfrac{1}{b^2} \quad だから$

$\quad 楕円 \qquad \cfrac{x^2}{a^2} + \cfrac{y^2}{b^2}=1 \quad では \quad A=\cfrac{1}{a^2},\ \ B=\cfrac{1}{b^2} \quad だから \quad y＝mx \pm \sqrt{a^2m^2+b^2}$

$\quad 双曲線 \qquad \cfrac{x^2}{a^2} - \cfrac{y^2}{b^2}=1 \quad では \quad A=\cfrac{1}{a^2},\ \ B=-\cfrac{1}{b^2} \quad だから \quad y＝mx \pm \sqrt{a^2m^2-b^2}$


$例1 \ \ 放物線 \ \ y^2=4px \ \ の直交する2本の接線の交点の軌跡$

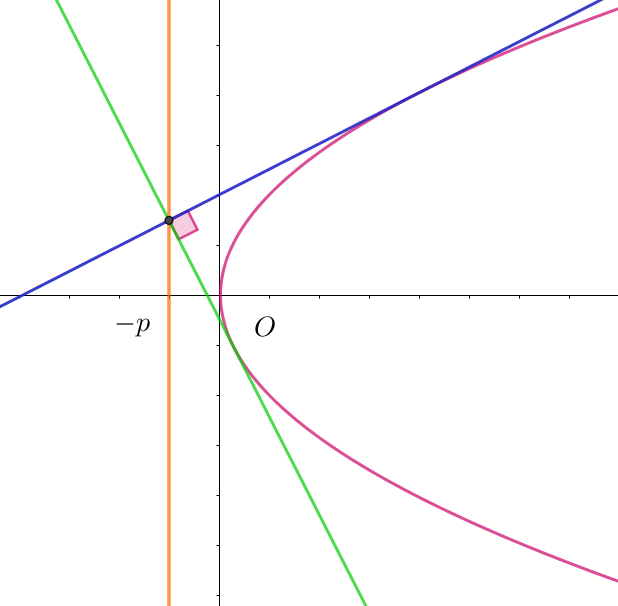　 $傾きmの接線は \quad y=mx+\cfrac{p}{m} \hspace{7em}(1)$

$これに直交する接線は \quad m \rightarrow -\cfrac{1}{m} \quad とおいて$

$\qquad y=-\cfrac{1}{m}x-pm \hspace{13em}(2)$

$交点はこの2式からmを消去すればよい。$

$(1)より \qquad my=m^2x+p$
$(2)より \qquad my=-x-pm^2$

$辺々引いて　\qquad (m^2+1)x+p(m^2+1)=0$

$\qquad (m^2+1)(x+p)=0 \qquad m^2+1 \ne 0 \quad だから \quad 　x=-p$

$これが求める軌跡で、放物線の準線である。$

$(別解)$

$\qquad y=mx+\cfrac{p}{m} \quad より \quad 　m^2x-my+p=0$

$このmについての2次方程式の解を \ m_1,\ m_2\ とすると、直交条件は \quad m_1m_2=-1$

$一方、解と係数の関係から \qquad 　m_1m_2=\cfrac{p}{x} \quad だから$

$\qquad \cfrac{p}{x}=-1 \qquad \therefore x=-p$


$例2 \ \ 楕円 \quad \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1 \quad の直交する2本の接線の交点の軌跡$

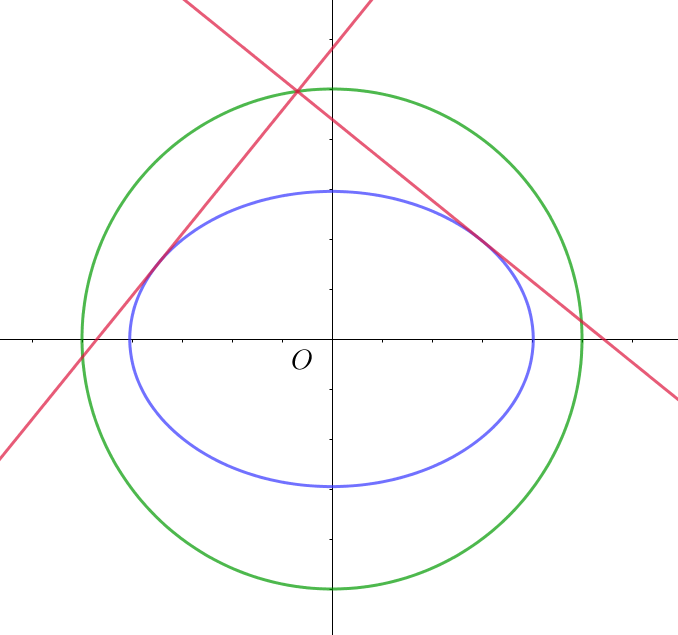　 $傾きmの接線は \quad y=mx \pm \sqrt{a^2m^2+b^2} \hspace{7em}(1)$

$これに直交する接線は \qquad m \rightarrow -\cfrac{1}{m} \quad とおいて$

$\qquad y=-\cfrac{1}{m}x \pm \sqrt{\cfrac{a^2}{m^2} +b^2} \hspace{13em}(2)$

$交点はこの2式からmを消去すればよい。$

$(1)より \qquad (y-mx)^2=a^2m^2+b^2$
$(2)より \qquad (my+x)^2=a^2+b^2m^2$

$辺々加えて \qquad 　(m^2+1)y^2+(m^2+1)x^2=(m^2+1)a^2+(m^2+1)b^2$

$m^2+1 \ne 0 \quad だから \quad これで割って \qquad x^2+y^2=a^2+b^2$

$これが求める軌跡で、原点中心、半径 \ \ \sqrt{a^2+b^2}\ \ の円である。$

$(別解)$

$\qquad y=mx \pm \sqrt{a^2m^2+b^2} \quad より \quad (y-mx)^2=a^2m^2+b^2$

$\qquad (x^2-a^2)m^2-2mxy+y^2-b^2=0$

$このmについての2次方程式の解を \ m_1,\ m_2\ とすると、直交条件は \qquad m_1m_2=-1$

$一方、解と係数の関係から \qquad m_1m_2=\cfrac{y^2-b^2}{x^2-a^2}\quad だから$

$\qquad \cfrac{y^2-b^2}{x^2-a^2}=-1 \qquad \therefore x^2+y^2=a^2+b^2$


$例3 \ \ 双曲線 \quad \cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1 \quad の直交する2本の接線の交点の軌跡$

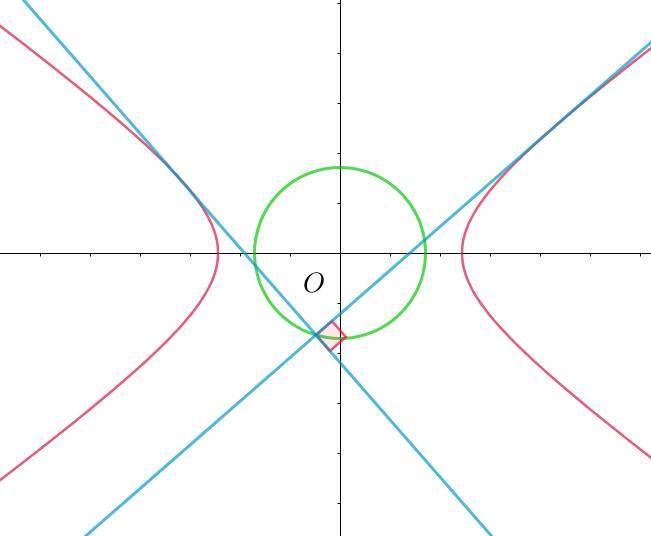　 $楕円と全く同様にして、原点中心、半径 \ \ \sqrt{a^2-b^2}\ \ の円となる。$

ページの先頭へ↑