信州大学(数学) 2025年 問題4
$(1)\ \ 関数 \ \ f(x)=\sin ^3x \cos x \ \ の区間 \ \ 0 \leqq x \leqq \pi \ \ における最大値、最小値と、そのときの \ x\ の値を$
$\quad それぞれ求めよ。$
$(2)\ \ (1)で求めた、最大値を与える \ x\ の値を \ a\ とする。$
\[\quad 定積分 \quad \int_0^a(3\sin^8 x\cos ^4x - \sin ^{10}x\cos ^2x)dx \quad を求めよ。\]
(1)
$f(x)=\sin ^3x \cos x より$
\begin{eqnarray*} f'(x) &=&3\sin ^2x \cos ^2x + \sin ^3x (-\sin x)\\ \\ &=&3\sin ^2x \cos ^2x - \sin ^4x \\ \\ &=&\sin ^2x (3\cos ^2x - \sin ^2x) \\ \\ &=&\sin ^2x \big(3(1-\sin ^2x) - \sin ^2x\big) \\ \\ &=&\sin ^2x (3-4\sin ^2x) \end{eqnarray*}
$ 0 \leqq x \leqq \pi \ \ における \ \ f'(x)=0\ \ の解は$
$\sin x=0 \quad より \quad x=0,\quad \pi$
$\sin x \geqq 0 \quad だから \quad \sin x=\dfrac{\sqrt{3}}{2}\quad より \quad x=\dfrac{\pi}{3},\quad \dfrac{2}{3}\pi$
$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & \dfrac{\pi}{3} & \cdots & \dfrac{2}{3}\pi & \cdots & \pi\\ \hline f'(x)& & + & 0 & - & 0 & + & \\ \hline f(x) & & \nearrow & 極大 & \searrow & 極小 & \nearrow & \\ \end{array} \]
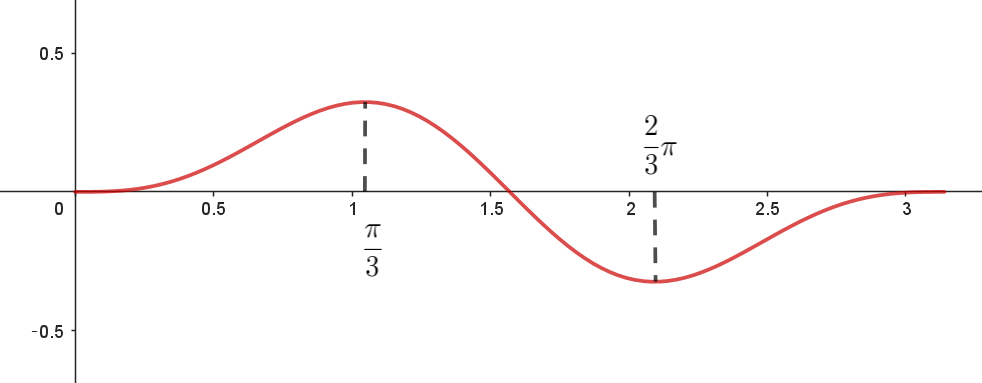
$x=\dfrac{\pi}{3} \ \ で極大かつ最大となり、最大値は$
$f(\dfrac{\pi}{3})=\big(\dfrac{\sqrt{3}}{2}\big)^3 \times \dfrac{1}{2}=\dfrac{3\sqrt{3}}{16}$
$x=\dfrac{2}{3}\pi \ \ で極小かつ最小となり、最小値は$
$f(\dfrac{2}{3}\pi)=\big(\dfrac{\sqrt{3}}{2}\big)^3 \times \big(-\dfrac{1}{2}\big)=-\dfrac{3\sqrt{3}}{16}$
$なお、y=f(x) \ \ のグラフは右図のとおりである。$
(2)
$定積分を \ I,被積分関数を \ J(x)\ \ とおくと$
$(1)より \quad a=\dfrac{\pi}{3}$
$f(x)=\sin ^3x \cos x , \quad f'(x)=3\sin ^2x \cos ^2x - \sin ^4x \quad だから$
\begin{eqnarray*} J(x) &=&3\sin^8 x\cos ^4x - \sin ^{10}x\cos ^2x\\ \\ &=&\sin^6x\cos^2x(3\sin^2x\cos^2x-\sin^4x)\\ \\ &=&\big(f(x)\big)^2f'(x) \end{eqnarray*}
$したがって$
\begin{eqnarray*} I &=&\int_0^aJ(x)dx\\ \\ &=&\int_0^a \big(f(x)\big)^2f'(x)dx\\ \\ &=&\big[\big(f(x)\big)^2f(x)\big]_0^a - \int_0^a \big(2f(x)f'(x)\big)f(x)dx\\ \\ &=&\big[\big(f(x)\big)^3\big]_0^a - 2\int_0^a \big(f(x)\big)^2f'(x)dx\\ \\ &=&\big(f(a)\big)^3 - \big(f(0)^3\big) - 2\int_0^a J(x)dx\\ \\ &=&\big(\dfrac{3\sqrt{3}}{16}\big)^3 -2I \end{eqnarray*} $3I=\big(\dfrac{3\sqrt{3}}{16}\big)^3$
$I=\dfrac{1}{3}\big(\dfrac{3\sqrt{3}}{16}\big)^3=\dfrac{27\sqrt{3}}{4096}$
$(別解)$
$J(x)=\big(f(x)\big)^2f'(x) \ \ の関係を見つけるのはかなりの洞察力が必要です。$
$おそらく多くの受験生は次のように漸化式を導いて解いたと思われます。$
\begin{eqnarray*} I_m &=&\int_0^a \sin^m xdx\\ \\ &=&\int_0^a \sin x \cdot \sin^{m-1} xdx\\ \\ &=&\big[-\cos x \cdot \sin^{m-1} x\big]_0^a + \int_0^a \cos x \cdot (m-1)\sin^{m-2} x \cdot \cos x dx\\ \\ &=&-\dfrac{1}{2}\big(\dfrac{\sqrt{3}}{2}\big)^{m-1}+(m-1)\int_0^a \cos ^2x \cdot \sin^{m-2} x dx\\ \\ &=&-\dfrac{1}{2}\big(\dfrac{\sqrt{3}}{2}\big)^{m-1}+(m-1)\int_0^a (1-\sin ^2x) \cdot \sin^{m-2} x dx\\ \\ &=&-\dfrac{1}{2}\big(\dfrac{\sqrt{3}}{2}\big)^{m-1}+(m-1)\big(I_{m-2}-I_m\big)\\ \end{eqnarray*}
$mI_m=-\dfrac{1}{2}\big(\dfrac{\sqrt{3}}{2}\big)^{m-1}+(m-1)I_{m-2}$
$\therefore \ \ I_m=-\dfrac{(\sqrt{3})^{m-1}}{m2^m} +\dfrac{m-1}{m}I_{m-2}$
\[ただし \quad I_0=\int_0^adx=a=\dfrac{\pi}{3}\]
$したがって$
\begin{eqnarray*} I &=&\int_0^a(3\sin^8 x\cos ^4x - \sin ^{10}x\cos ^2x)dx\\ \\ &=&\int_0^a(3\sin^8 x(1-\sin ^2x)^2 - \sin ^{10}x(1-\sin ^2x)dx\\ \\ &=&\int_0^a(3\sin^8 x(1-2\sin ^2x+\sin^4 x) - \sin ^{10}x(1-\sin ^2x)dx\\ \\ &=&\int_0^a(4\sin^{12}x -7\sin ^{10}x+3\sin^8 x)dx\\ \\ &=&4I_{12}-7I_{10}+3I_8\\ \\ &=&4 \times \big(-\dfrac{(\sqrt{3})^{11}}{12\cdot 2^{12}} +\dfrac{11}{12}I_{10}\big)-7I_{10}+3I_8\\ \\ &=&-\dfrac{3^5\sqrt{3}}{3 \cdot 2^{12}} +\dfrac{11}{3}I_0 -7I_{10}+3I_8\\ \\ &=&-\dfrac{3^4\sqrt{3}}{2^{12}} -\dfrac{10}{3}I_{10}+3I_8\\ \\ &=&-\dfrac{81\sqrt{3}}{2^{12}} - \dfrac{10}{3}\big\{-\dfrac{(\sqrt{3})^9}{10 \cdot 2^{10}} +\dfrac{9}{10}I_8\big\}+3I_8\\ \\ &=&-\dfrac{81\sqrt{3}}{2^{12}} + \dfrac{3^4\sqrt{3}}{3 \cdot 2^{10}} -3I_8+3I_8\\ \\ &=&-\dfrac{81\sqrt{3}}{2^{12}} + \dfrac{3^3\sqrt{3}}{2^{10}}\\ \\ &=&\dfrac{-81\sqrt{3} +108\sqrt{3}}{2^{12}}\\ \\ &=&\dfrac{27\sqrt{3}}{2^{12}}\\ \\ &=&\dfrac{27\sqrt{3}}{4096}\\ \end{eqnarray*}
メインメニュー に戻る