信州大学(数学) 2025年　問題2


$関数 \ \ f(t)=3 \cdot 2^{t+2} +2\cdot 4^{t+1} -8^t \ \ の区間 \ \ 0 \leqq t \leqq 3 \ \ における最大値、最小値と、そのときの \ t\ の値を$
$それぞれ求めよ。$


\begin{eqnarray*} f(t) &=&3 \cdot 2^{t+2} +2\cdot 4^{t+1} -8^t\\ \\ &=&12 \cdot 2^t +8 \cdot 4^t -8^t\\ \\ &=&12 \cdot 2^t +8 \cdot 2^{2t} -2^{3t}\\ \\ &=&12 \cdot 2^t +8 \cdot (2^{t})^2 -(2^{t})^3 \end{eqnarray*}
$2^t=u \ \ とおくと \quad 0 \leqq t \leqq 3 \ \ だから \quad 1 \leqq u \leqq 8$

$このとき \ \ f(t)\ \ を \ \ g(u) \ \ とおくと$

$g(u)=12u +8 u^2 -u^3=-u^3+8u^2+12u$

$g'(u)=-3u^2+16u+12=-(3u^2-16u-12)=-(u-6)(3u+2)$

$g'(u)=0 \quad より \quad u=6$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} u& 1 & \cdots & 6 & \cdots & 8\\ \hline g'(u)& & + & 0 & - & \\ \hline g(u) & & \nearrow & 極大 & \searrow & \\ \end{array} \]

　

$u=6 \ \ で極大となり、極大値は $

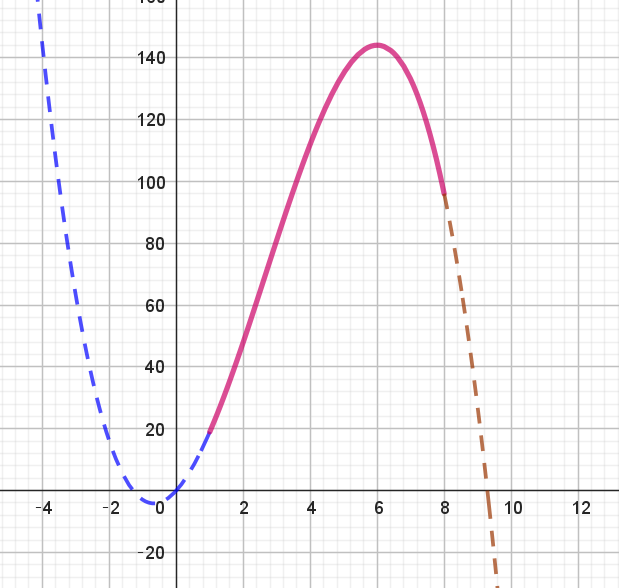
$g(6)=-6^3+8 \times 6^2+12 \times 6=144$

$g(1)=-1+8+12=19$

$g(8)=-8^3+8^3+12 \times 8=96$

$y=g(u) のグラフは右図のとおりである。$

$したがって$

$u=1 \ \ すなわち \quad t=0 \ \ のとき最小値 \ \ 19\ \ をとり$

$u=6 \ \ すなわち \quad t=\log_2 6 \ \ のとき最大値 \ \ 144\ \ をとる。$


ページの先頭へ↑



メインメニュー　に戻る