信州大学(数学) 2025年　問題1


$四面体OABC\ において、\vec{a}=\vec{OA},\ \ \vec{b}=\vec{OB},\ \ \vec{c}=\vec{OC}\ \ とおく。線分OA\ を \ 1:2\ に内分する点を \ D,\ 線分OB\ を$
$3:2\ に内分する点を \ E,\ \ 線分OC\ を \ 1:1\ に内分する点を \ F\ とする。また、三角形ABC\ の重心を \ G\ とし、$
$四面体OABC\ の体積を \ V\ とする。$
$(1)\ \ 3\ 点D,\ E,\ F\ を含む平面と線分OG\ との交点を \ P\ とする。\vec{p}=\vec{OP} \ \ とおくとき \ \ \vec{p}\ を \ \vec{a},\ \ \vec{b},\ \ \vec{c}\ を用いて$
$\quad 表せ。$
$(2)\ \ 四面体ODEF\ の体積を \ V\ を用いて表せ。$
$(3)\ \ 四面体GDEF\ の体積を \ V\ を用いて表せ。$

(1)

　

$点P\ は平面DEF 上にあるから$

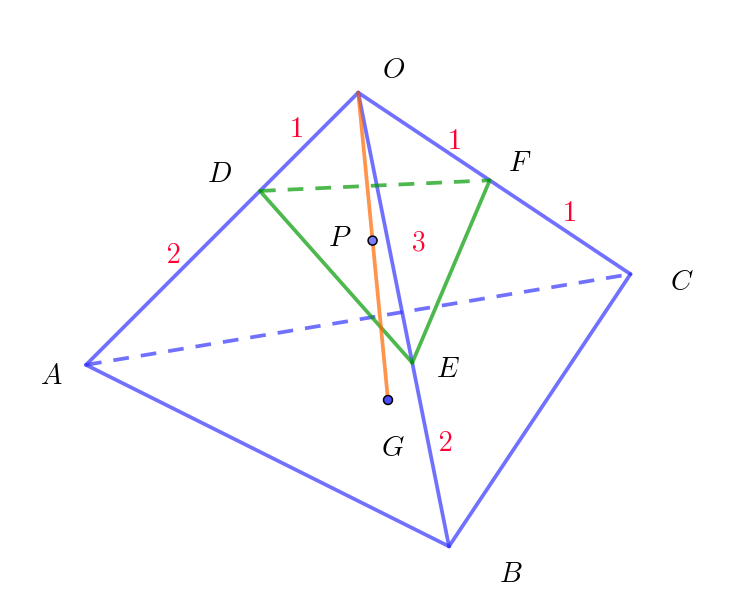
$\vec{DP}=\alpha \vec{DE} + \beta \vec{DF} \ \ を満たす実数 \ \alpha ,\ \ \beta \ \ が存在する。$

$\vec{OP}- \vec{OD}=\alpha (\vec{OE} -\vec{DF})+ \beta (\vec{OF} - \vec{OD}) $

$\vec{OP}=(1-\alpha - \beta )\vec{OD} + \alpha \vec{OE} + \beta \vec{OF} $

\begin{eqnarray*} \vec{p} &=&(1-\alpha - \beta ) \times \dfrac{1}{3}\vec{a} + \alpha \times \dfrac{3}{5}\vec{b} + \beta \times \dfrac{1}{2}\vec{c}\\ \\ &=&\dfrac{1}{3}(1-\alpha - \beta ) \vec{a} + \dfrac{3}{5}\alpha \vec{b} + \dfrac{1}{2}\beta \vec{c}　\hspace{5em}①\\ \end{eqnarray*}
$一方、3\ 点 \ O,\ P,\ G\ は一直線上にあるから \ \ \vec{OP}=k\vec{OG}\ \ (k\ は実数)\ \ とおける。$

$また、点G\ は三角形ABC\ の重心だから \quad \vec{OG}=\dfrac{1}{3}(\vec{a}+\vec{b}+\vec{c})$

$よって、\vec{p}=\dfrac{k}{3}(\vec{a}+\vec{b}+\vec{c}) \hspace{5em}②$

$①，②より \quad \dfrac{1}{3}(1-\alpha - \beta ) \vec{a} + \dfrac{3}{5}\alpha \vec{b} + \dfrac{1}{2}\beta \vec{c}=\dfrac{k}{3}(\vec{a}+\vec{b}+\vec{c})$

$\vec{a},\ \vec{b},\ \vec{c}\ \ は同一平面上になく、互いに平行でない \ \ (一次独立といいます)\ \ から$
\[ \hspace{1em} \left\{ \begin{array}{l} \dfrac{1}{3}(1-\alpha - \beta ) =\dfrac{k}{3} \hspace{4.5em}③\\ \dfrac{3}{5}\alpha = \dfrac{k}{3} \hspace{9em}④\\ \dfrac{1}{2}\beta=\dfrac{k}{3} \hspace{9em}⑤\\ \end{array} \right. \]
$④、⑤より \quad \alpha=\dfrac{5}{9}k,\quad \beta =\dfrac{2}{3}k$

$これらを③に代入して \quad 1-\dfrac{5}{9}k-\dfrac{2}{3}k=k$

$これを解いて \quad k=\dfrac{9}{20}$

$よって \quad \vec{p}=\dfrac{3}{20}(\vec{a}+\vec{b}+\vec{c})$


(2)

　

$四面体OABC\ \ と \ \ ODEF\ \ の体積は、底面をそれぞれ$

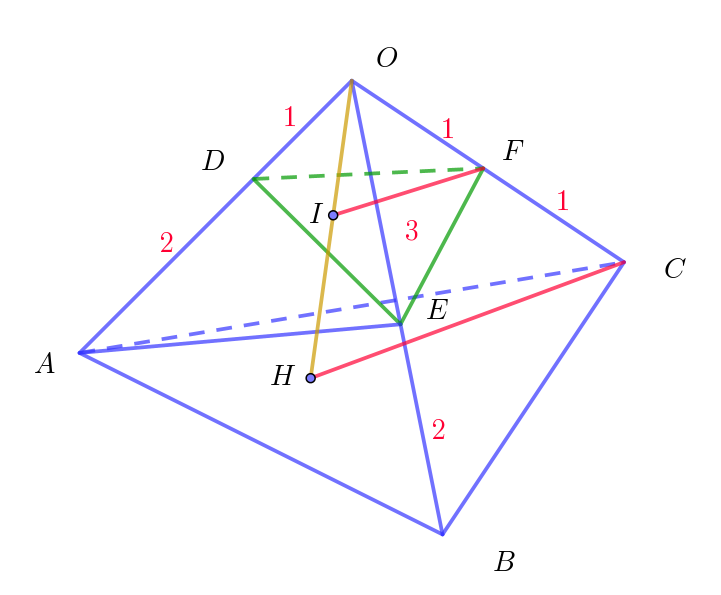
$\triangle OAB,\ \ \triangle ODE \ \ と考える。$

$\triangle ODE=S \ \ とおくと$

$OD:OA=1:3 \ \ より \quad \triangle OAE=3S$

$OE:OB=3:5 \ \ より \quad \triangle OAB=5S$

$点F,\ C\ \ から底面 \ \triangle OAB\ \ に下ろした垂線を$

$それぞれ \ \ FI,\ \ CH \ \ とすると \quad FI /\!/ CH $

$平行な2直線で決まる平面OHC\ と底面 \ \triangle OAB \ \ の交わりは$

$直線であるから、3\ 点 \ O,\ I,\ H\ は一直線上にある。$

$\triangle OIF ∽ \triangle OHC \ \ で、OF:OC=1:2 \ \ だから \quad FI:CH=1:2$

$四面体ODEF \ \ の体積を \ V_1\ \ とすると$

$\dfrac{V_1}{V}=\dfrac{\triangle ODE }{\triangle OAB} \times \dfrac{FI}{CH}=\dfrac{1}{5} \times \dfrac{1}{2}=\dfrac{1}{10}$

$したがって \quad 四面体ODEF\ の体積 \ \ V_1=\dfrac{1}{10}V$


(3)

　

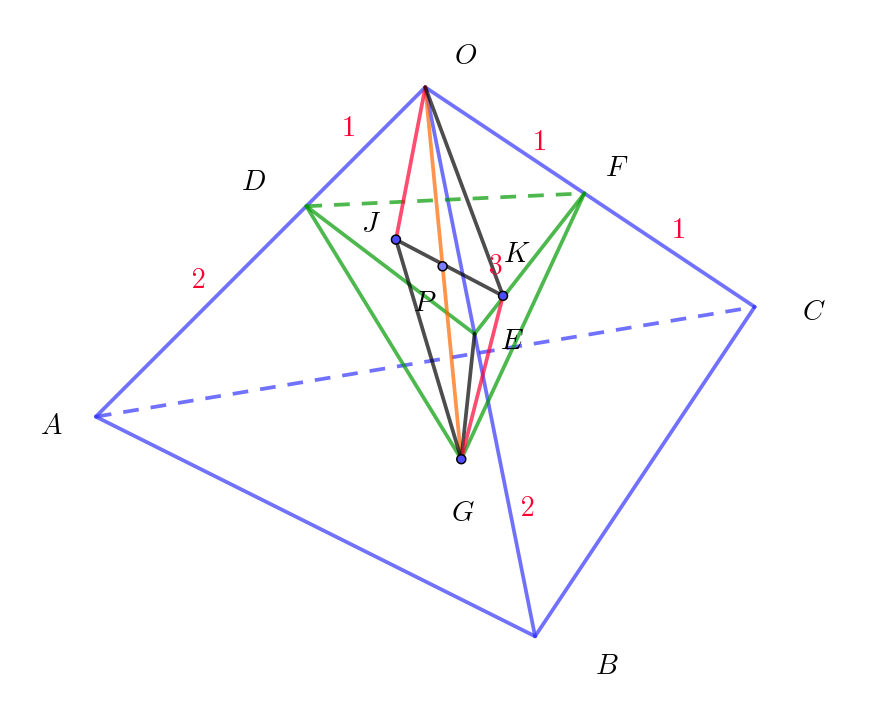
$四面体ODEF \ と \ \ GDEF\ \ の体積は、底面を \ \ \triangle DEF$

$と考える。$

$点O,\ \ G\ から底面 \ \triangle DEF\ \ に下ろした垂線を$

$それぞれ \ \ OJ,\ \ GK \ \ とすると \quad OJ /\!/ GK $

$平行な \ 2\ 直線で決まる平面 \ OJGK \ と底面 \ \triangle DEF\ \ の$

$交わりは直線であるから、3\ 点 \ J,\ P,\ K\ は一直線上にある。$

$\triangle OJP ∽ \triangle GKP \ で、OP:OG=\dfrac{9}{20}:1=9:20 $

$ OJ:GK=OP:GP=9:11 $

$したがって \quad 四面体GDEF \ の体積 \ \ V_2=\dfrac{11}{9} \times 四面体ODEF=\dfrac{11}{9} \times \dfrac{1}{10}V=\dfrac{11}{90}V$


ページの先頭へ↑



メインメニュー　に戻る